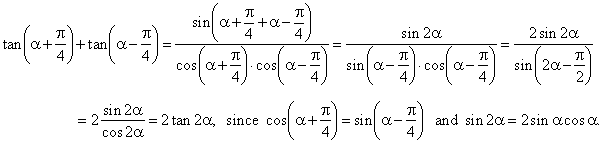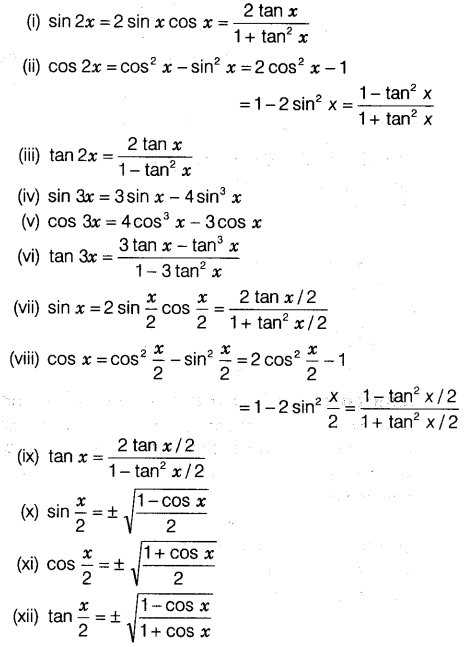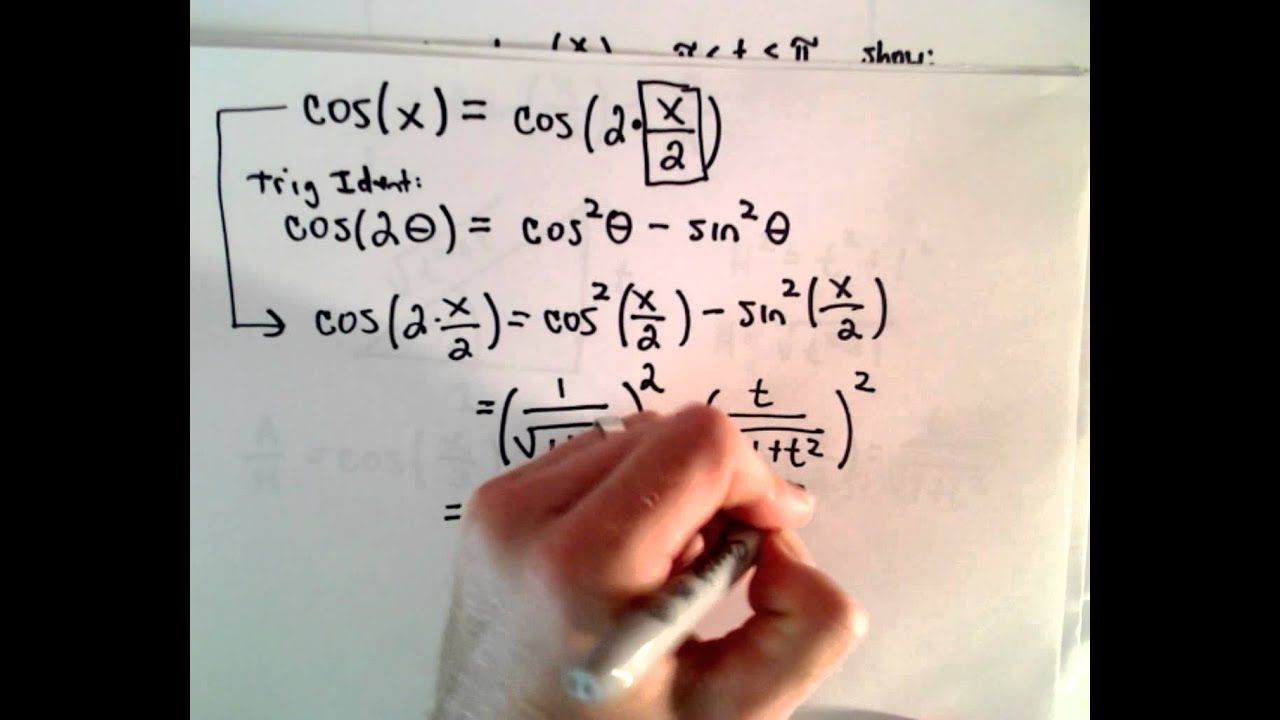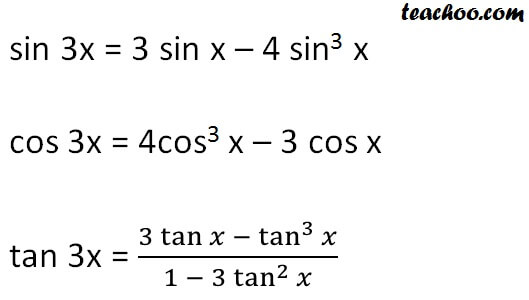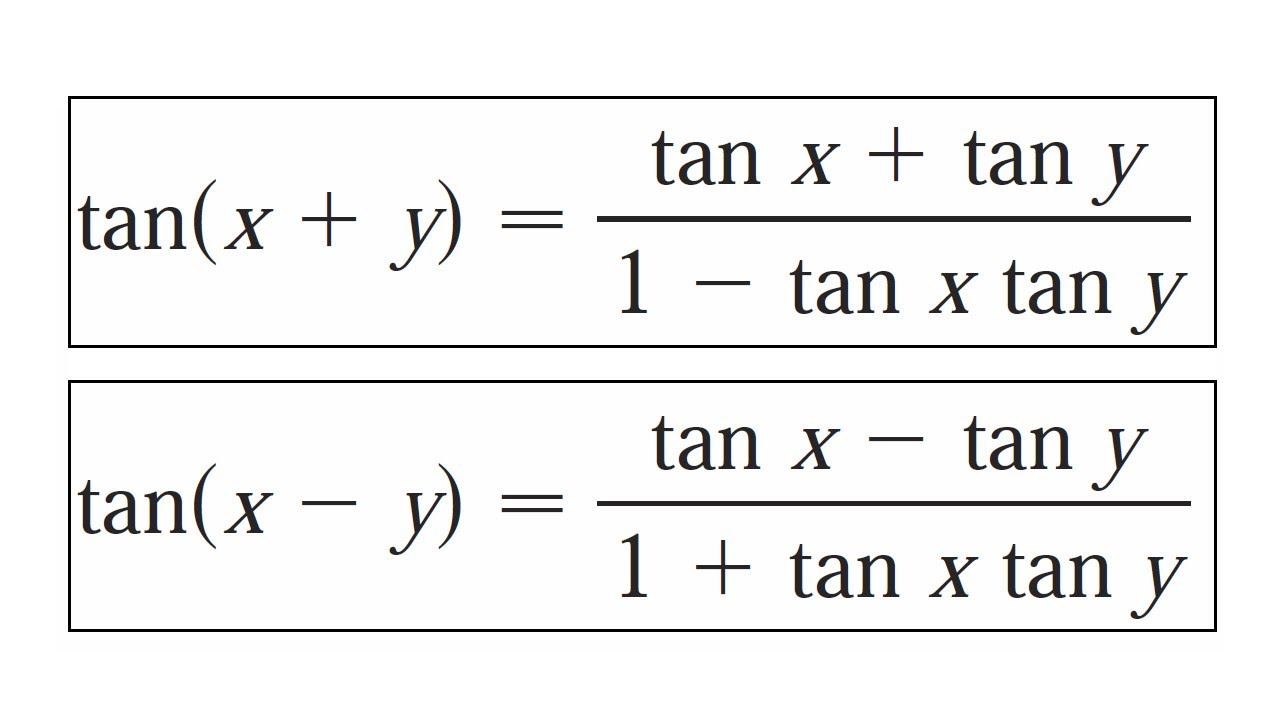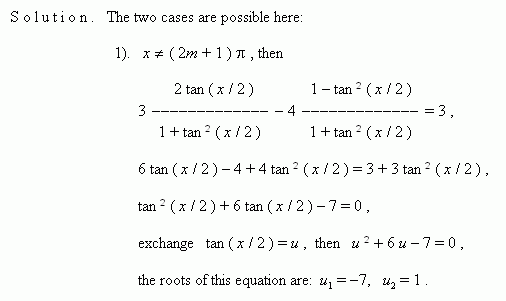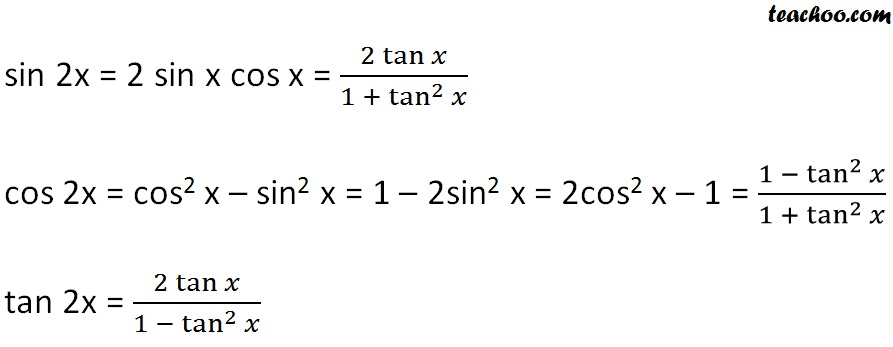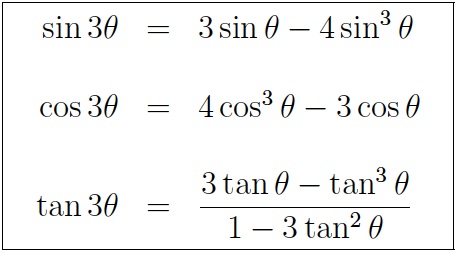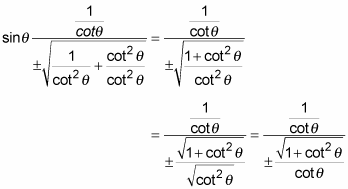Cos X Formula In Terms Of Tan
Weierstrass Substitution Wikipedia
en.wikipedia.org
Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube
www.youtube.com
Properties Of A Inverse Trigonometric Function Tutorsonnet
www.tutorsonnet.com
Solved Section 7 3 Double Angle Half Angle And Product Chegg Com
www.chegg.com
Inverse Trigonometric Functions Wikipedia
en.wikipedia.org
What Is The Formula Of Tan2x Quora
www.quora.com
Cos 2a cos2 a sin2acos2 a cos2 a cos 2a cos2 a 1 tan2 a cos 2a 1sec2 a 1 tan2 a cos 2a 1 tan2 a1 tan2 a.
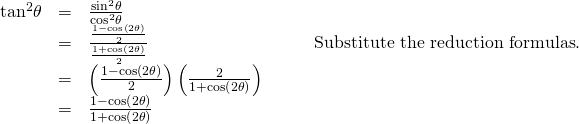
Cos x formula in terms of tan. Sine cosine and tangent often shortened to sin cos and tan are each a ratio of sides of a right angled triangle. Now multiply through by cos x cos x giving. The notations sin 1 x cos 1 x tan 1 x etc as introduced by john herschel in 1813 are often used as well in english language sources conventions consistent with the notation of an inverse function.
Eulers formula named after leonhard euler is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential functioneulers formula states that for any real number x. We know that cos 1 sec so this can be written. 2 sin x cos x 1 sec2 x.
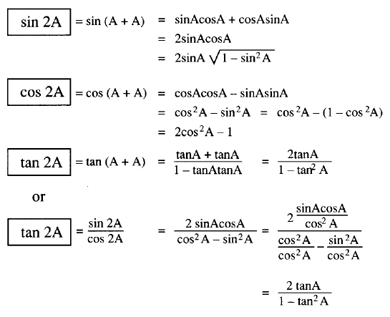
We know if a is a number or angle then we have cos 2a cos2 a sin2 a. Which can be written. For a given angle o each ratio stays the same no matter how big or small the triangle is.
Sin 2 o sine squared theta means sin o 2. To cover the answer again click refresh reload. These can be derived geometrically using arguments that date to ptolemy.
A 3 4 5 triangle is right angled. 2 sin x cos x. One can also produce them algebraically using eulers formula.
A half turn or 1800 or p radian is the period of tanx sinx cosx and cotx cosx sinx as can be seen from these definitions and the period of the defining trigonometric functions. To see the answer pass your mouse over the colored area. The first shows how we can express sin o in terms of cos o.
The sum and difference formulas allow expanding the sine the cosine and the tangent of a sum or a difference of two angles in terms of sines and cosines and tangents of the angles themselves. We know sin x cos x tan x and sec2 1 tan2 so we get. Trigonometric function of cos 2a in terms of tan a is also known as one of the double angle formula.
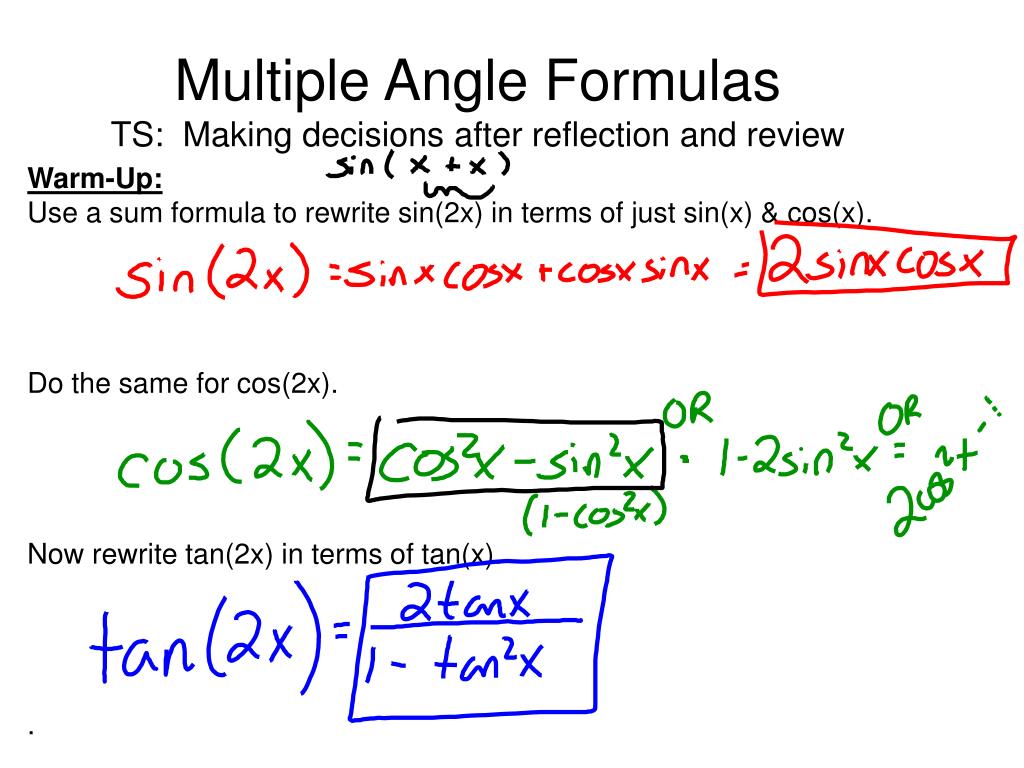
2 sin x cos x cos2 x. Expand out sin 2x using the double angle formula you get. In various applications of trigonometry it is useful to rewrite the trigonometric functions such as sine and cosine in terms of rational functions of a new variable tthese identities are known collectively as the tangent half angle formulae because of the definition of tthese identities can be useful in calculus for converting rational functions in sine and cosine to functions of t in.
Where e is the base of the natural logarithm i is the imaginary unit and cos and sin are the trigonometric functions. Therefore shifting the arguments of tanx and cotx by any multiple of p does not change their function values. Sine cosine and tangent.
Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities
www.nabla.hr
Solved Prove The Identity Cotx Tan X Cos 2x Sin X Cos Chegg Com
www.chegg.com
Solved Problem 4 Using The Sin And Cos Addition Formulas Chegg Com
www.chegg.com
Tangent Half Angle Formula Wikipedia
en.wikipedia.org
Tan 3x In Terms Of Tan X Youtube
www.youtube.com
List Of Integrals Of Trigonometric Functions Wikipedia
en.wikipedia.org
How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube
www.youtube.com
Tangent Half Angle Formula Wikipedia
en.wikipedia.org
Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id 3998440
www.slideserve.com
Trigonometric Functions Class 11 Notes Maths Chapter 3 Learn Cbse
www.learncbse.in
What Are The Formulas Of Sin 2x Quora
www.quora.com
What Are The Formulas Of Cos 2x Quora
www.quora.com
Solved A Use The Power Series For Cos X To Compute The Chegg Com
www.chegg.com
Cbse 10 Math Cbse Introduction To Trigonometry Ncert Solutions
www.careerlauncher.com
2
Misc 13 Solve 2 Tan 1 Cos X Tan 1 2 Cosec X Miscellaneous
www.teachoo.com
Double Angle Half Angle And Reduction Formulas Algebra And Trigonometry
opentextbc.ca
Small Angle Approximation Brilliant Math Science Wiki
brilliant.org
Summary Of Trigonometric Identities
www2.clarku.edu
Cbse 10 Math Cbse Introduction To Trigonometry Ncert Solutions
www.careerlauncher.com
How To Rewrite Math Sin 4 X Math So That It Involves Only The First Power Of Cosine Quora
www.quora.com
Half Angle Formulas Power Reducing Formulas 2x 3x Formula Provin
www.teachoo.com
Ex 2 2 13 Inverse Trigonometry Tan 1 2 Sin 1 2x 1 X2
www.teachoo.com
How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube
m.youtube.com
Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2
www.teachoo.com
Ex 2 2 8 Chapter 2 Class 12 Inverse Tan 1 Cos X Sin X
www.teachoo.com
Summary Of Trigonometric Identities
www2.clarku.edu
Integrate Rational Function Of Sine And Cosine T Tan X 2 Part 1 Youtube
www.youtube.com
Triple Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
www.teachoo.com
Derivatives Of Trigonometric Functions
www.math24.net
Please Solve Question Number 15 As Soon As Possible Cos68 In Terms Of Os9 Iii Express Tan40 In Math Some Applications Of Trigonometry 11630315 Meritnation Com
www.meritnation.com
Solved Use The Power Reducing Formulas To Rewrite Tan X C Chegg Com
www.chegg.com
Misc 9 Prove Tan 1 Root X 1 2 Cos 1 1 X 1 X
www.teachoo.com
Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com
www.chegg.com
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com
Math34 Trigonometric Formulas
www.slideshare.net
By Parts Integration By Parts Although Integration By Parts Is Used Most Of The Time On Products Of The Form Described Above It Is Sometimes Effective Ppt Download
slideplayer.com
Answered 19 Cos X Cos 2x 0 20 Sin X Cos 2x Bartleby
www.bartleby.com
Solved 1 Point Use C To Denote Cos X And Express 1 Tan Chegg Com
www.chegg.com
What Is The Formula Of Tan2x Quora
www.quora.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcsr4 S2mwqyyvcchtc3gopfh7qymvafk7mrnbovstzrqefeajoc Usqp Cau
encrypted-tbn0.gstatic.com
Misc 13 Solve 2 Tan 1 Cos X Tan 1 2 Cosec X Miscellaneous
www.teachoo.com
Summary Of Trigonometric Identities
www2.clarku.edu
How Is Secx Tanx Tan P 4 X 2 Quora
www.quora.com
Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube
www.youtube.com
Trigonometric Identities Topics In Trigonometry
themathpage.com
Integrals Of Trigonometric Functions Web Formulas
www.web-formulas.com
Example 12 Express Cos A Tan A And Sec A In Terms Of Sin A
www.teachoo.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcr Qbuprpojkb9oto7vayo7s67hh0h2efq2yxn8siadklmutoec Usqp Cau
encrypted-tbn0.gstatic.com
Tangent Half Angle Formula Wikipedia
en.wikipedia.org
Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2
www.teachoo.com
Tangent Identities
www.cliffsnotes.com
Important Trigonometric Identiti
www.pstcc.edu
Solved 2 Use The Substitution U Tan 3 2 To Compute Th Chegg Com
www.chegg.com
Example 5 Express Tan 1 Cos X 1 Sin X Chapter 2 Inverse
www.teachoo.com
Tangent Half Angle Formula Wikipedia
en.wikipedia.org
Expressing Sin X And Cos X In Terms Of Tan X Youtube
www.youtube.com
Tangent Half Angle Formula Wikipedia
en.wikipedia.org
Solved Verify Each Identity You Must Show All Steps Pr Chegg Com
www.chegg.com
Trigonometric Functions Introduction Sine Cosine Videos And Examples
www.toppr.com
Solved Write Tan Cos 1 1 X Sin 1 Y In Terms Of X Chegg Com
www.chegg.com
What Are Sine Cosine And Tangent
www.quickanddirtytips.com
Summary Of Trigonometric Identities
www2.clarku.edu
Trigonometric Identity Tan X Y Proof Youtube
www.youtube.com
Express All The Trigonometric Ratios In Terms Of Tan 8 With Calculations Brainly In
brainly.in
hi.wikipedia.org
Write Cos2x In Terms Of Tanx Double Angle Transformation Youtube
www.youtube.com
Section 4 Sine And Cosine Rule
www.cimt.org.uk
Ex 8 4 1 Express Sin A Sec A And Tan A In Terms Of Cot A
www.teachoo.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcsnqaeuwthzkr4i35dmt5emosevrtmjcsi Hqstbtyzz2erx2t8 Usqp Cau
encrypted-tbn0.gstatic.com
Math34 Trigonometric Formulas
www.slideshare.net
All Elementary Mathematics Study Guide Trigonometry Trigonometric Equations Main Methods For Solving
www.bymath.com
What Is The Formula Of Tan2x Quora
www.quora.com
Example 5 Express Tan 1 Cos X 1 Sin X Chapter 2 Inverse
www.teachoo.com
Weierstrass Substitution Wikipedia
en.wikipedia.org
Compound Angle Identity Tan 3x Formula Derivation Youtube
www.youtube.com
Tangent Half Angle Formula Wikipedia
en.wikipedia.org
Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
www.teachoo.com
Sec2x In Terms Of Tanx Trig Identity A4 Youtube
www.youtube.com
Math34 Trigonometric Formulas
www.slideshare.net
Summary Of Trigonometric Identities
www2.clarku.edu
Section 7 3 Double Angle Half Angle And Sum
studylib.net
Trigonometric Functions Wikipedia
en.wikipedia.org
Express Sine In Terms Of Cotangent Dummies
www.dummies.com
Important Trigonometric Identiti
www.pstcc.edu
Trigonometric Functions Wikipedia
en.wikipedia.org
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcsr4 S2mwqyyvcchtc3gopfh7qymvafk7mrnbovstzrqefeajoc Usqp Cau
encrypted-tbn0.gstatic.com
Misc 9 Prove Tan 1 Root X 1 2 Cos 1 1 X 1 X
www.teachoo.com
Summary Of Trigonometric Identities
www2.clarku.edu
New Page 1
www.pstcc.edu
Solved Letting Y Tan 4 Theta And X Tan Theta Express Chegg Com
www.chegg.com
Biomath Trigonometric Functions
www.biology.arizona.edu
What Is Tan Cos Inverse Of X Quora
www.quora.com
Summary Of Trigonometric Identities
www2.clarku.edu
Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Download
slideplayer.com
Inverse Trigonometric Functions Wikipedia
en.wikipedia.org
Slide Fundamental Identities 5 2 Verifying Trigonometric Identities 5 3 Sum And Difference Identities For Cosine 5 4 Sum And Difference Identities Ppt Download
slideplayer.com
How To Solve The Equation 1 Cosx Tanx Sinx Quora
www.quora.com
