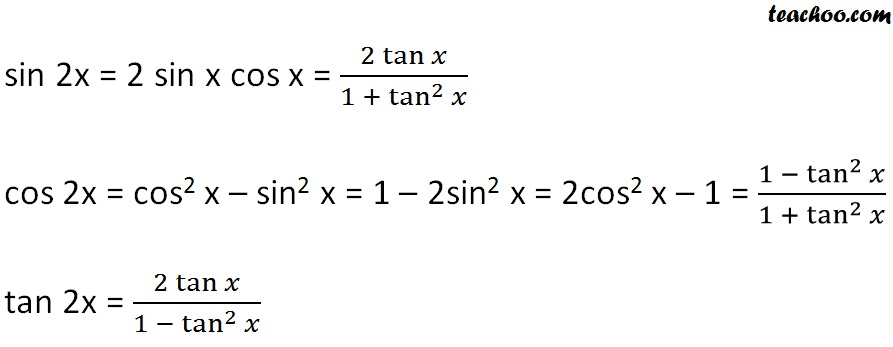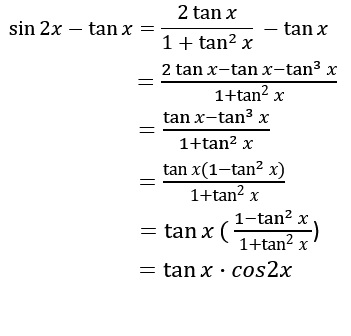Cos 2x Formula In Terms Of Tan X
These can be derived geometrically using arguments that date to ptolemy.

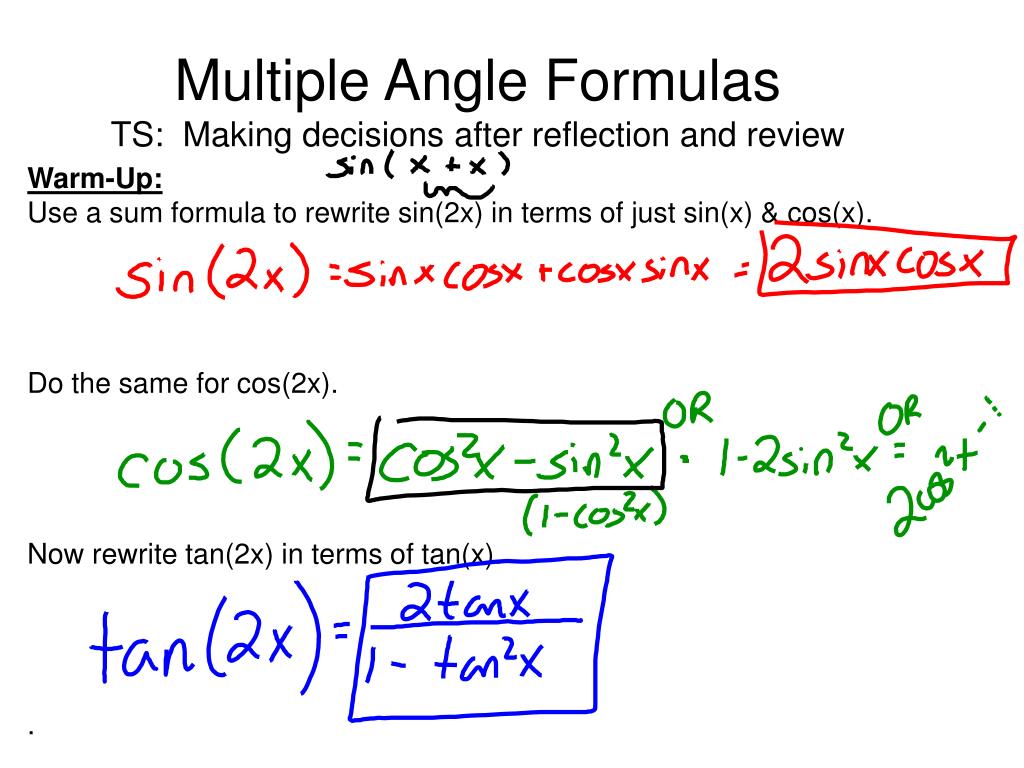
Cos 2x formula in terms of tan x. 2 1 tan2 x 1. Cos 2a cos2 a sin2acos2 a cos2 a cos 2a cos2 a 1 tan2 a cos 2a 1sec2 a 1 tan2 a cos 2a 1 tan2 a1 tan2 a. Cos 2 a cos2a sin2a 2cos2a 1.
Tan2x sin2xcos2x since cos2x 1 2sin2x therefore tan2x sin2x 1 2sin2x is it possible to do it in terms of cos x alone. We know sec2 1 tan2 so. I wanted to find tan2x in terms of cos x alone.
One can also produce them algebraically using eulers formula. We know if a is a number or angle then we have cos 2a cos2 a sin2 a. A half turn or 1800 or p radian is the period of tanx sinx cosx and cotx cosx sinx as can be seen from these definitions and the period of the defining trigonometric functions.
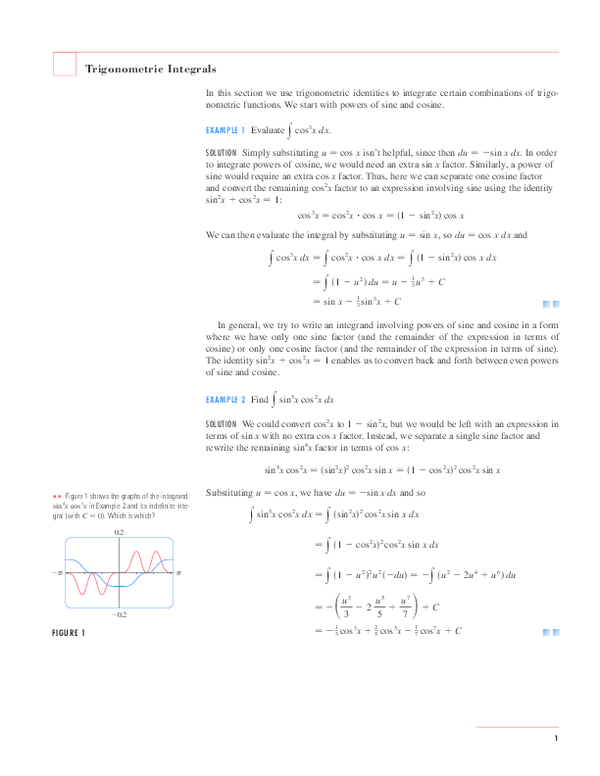
Cos2x 1 2sin 2 x 2cos 2 x 1 tan2x 2tanx 1 tan 2 x multiple angle formulas sin3x 3sinx 4sin 3 x cos3x 4cos 3 x 3cosx sin4x 4sinxcosx 8sin 3 xcosx cos4x 8cos 4 x 8cos 2 x 1 half angle formulas sin x2 or 1 cosx 2 cos x2 or 1 cosx 2 tan x2 or 1 cosx 1 cosx sinx 1 cosx 1 cosx sinx power reducing formulas sin 2 x 12 12cos2x. Expand out cos 2x using the double angle formula as 2 cos2 x 1. Trigonometric function of cos 2a in terms of tan a is also known as one of the double angle formula.
2 sec2 x 1. The sum and difference formulas allow expanding the sine the cosine and the tangent of a sum or a difference of two angles in terms of sines and cosines and tangents of the angles themselves. I was able to do it in terms of sin x alone.




















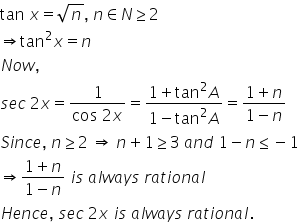





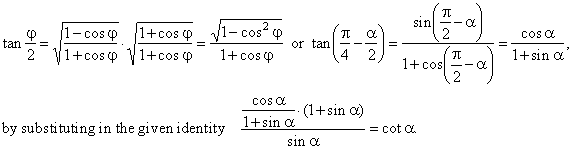





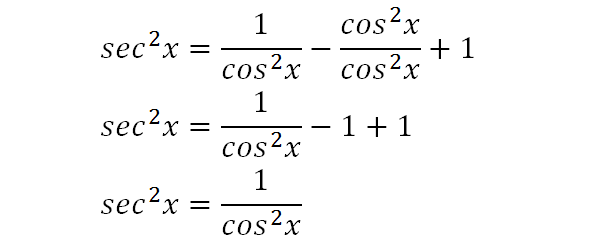




























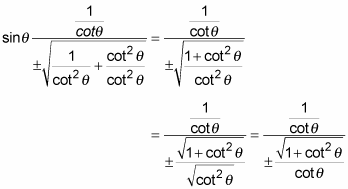

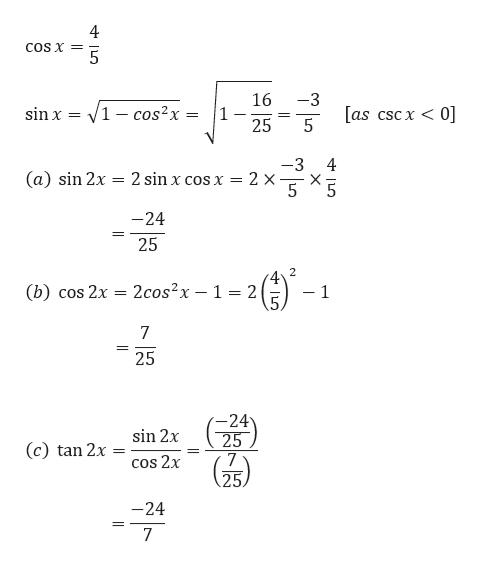



x-1=sec(squared)x.jpg)