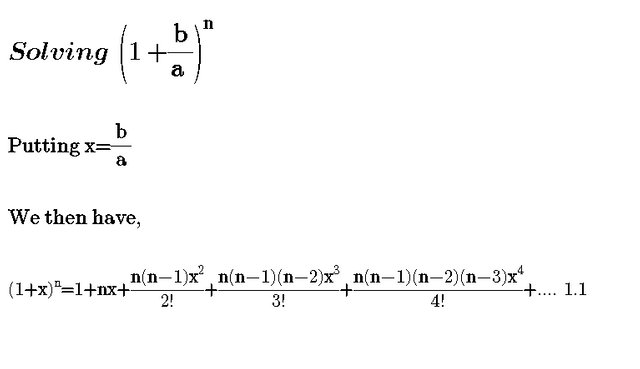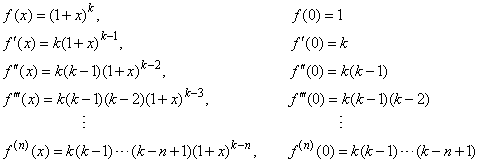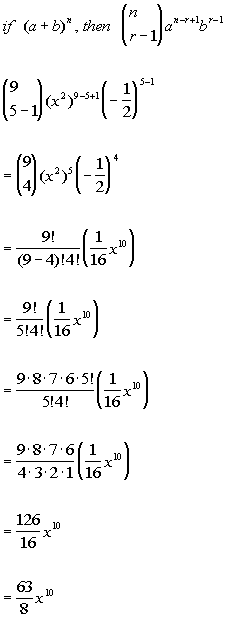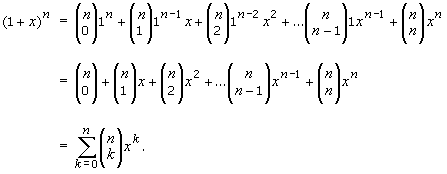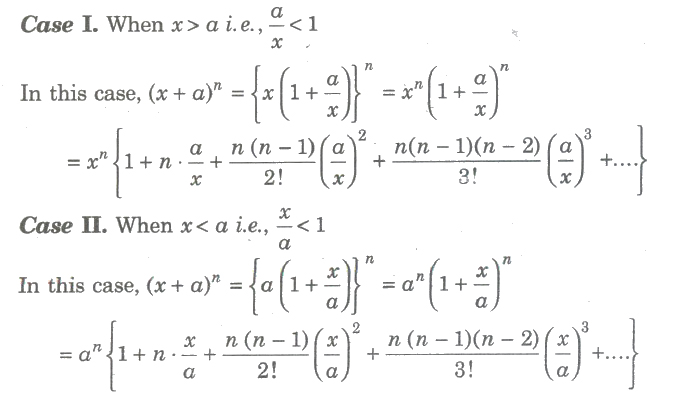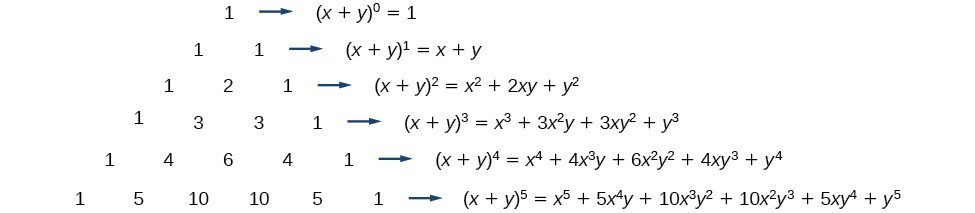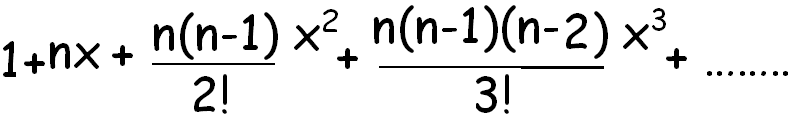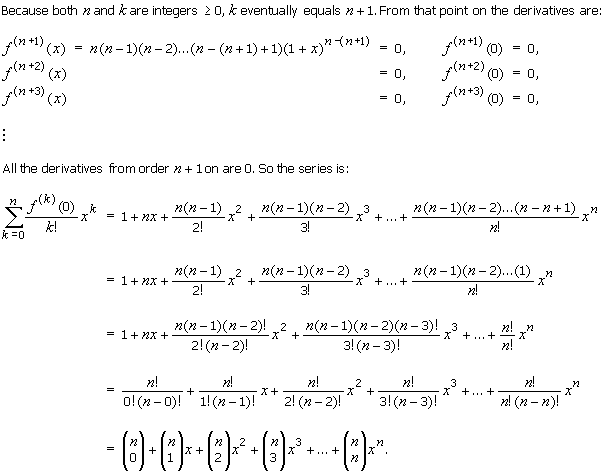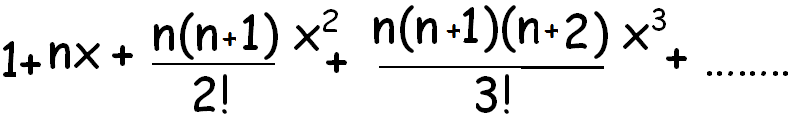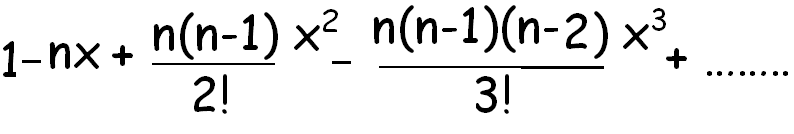Binomial Formula 1xn
Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf
byjus.com
Use The Binomial Theorem To Prove The Formula For The Derivative Of X N Stumbling Robot
www.stumblingrobot.com
Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange
math.stackexchange.com
Deriving Of Binomial Expansion Formula For Two Variables A B N Steemit
steemit.com
The Binomial Theorem Fractional Powers Expanding 1 2x 1 3 Youtube
www.youtube.com
Pascal S Triangle Wikipedia
en.wikipedia.org
Expand 4 2x 6 in ascending powers of x up to the term in x 3.
Binomial formula 1xn. So lets use the binomial theorem. This means use the binomial theorem to expand the terms in the brackets but only go as high as x 3. The benefit of this approximation is that is converted from an exponent to a multiplicative factor.
With just those first few terms we get e 27083. This can greatly simplify mathematical expressions as in the example below and is a. The binomial approximation is useful for approximately calculating powers of sums of 1 and a small number xit states that it is valid when and where and may be real or complex numbers.
Binomial theorem statement that for any positive integer n the nth power of the sum of two numbers a and b may be expressed as the sum of n 1 terms of the form. In elementary algebra the binomial theorem or binomial expansion describes the algebraic expansion of powers of a binomialaccording to the theorem it is possible to expand the polynomial x y n into a sum involving terms of the form ax b y c where the exponents b and c are nonnegative integers with b c n and the coefficient a of each term is a specific positive integer depending. Some expansions are as follows.
First we can drop 1 n k as it is always equal to 1. Here it represents the product of all the whole numbers between 1 and n. The binomial theorem states that where n is a positive integer.
The expression of the binomial theorem formula is given as follows. The coefficients called the binomial coefficients are defined by the formula. Xynsumk0n n choose k xn k yk also recall that the factorial notation n.
1 1n n it gets more accurate the higher the value of n that formula is a binomial right. We can write down the binomial expansion of 1xn as 1dfracn1x dfracnn 12x2 dfracnn 1n 23x3 this is true for all real.
10 6 The Binomial Series
www.geocities.ws
Solved Use The Binomial Series Formula To Find The Coeffi Chegg Com
www.chegg.com
Binomial Coefficients Inclusion Exclusion Principle Ppt Video Online Download
slideplayer.com
Example 6 Show That Middle Term In Expansion Of 1 X 2n Is
www.teachoo.com
Binomial Expansions 1 X N A B N N C 0 A N N C 1 A N 1 B N C 2 A
slideplayer.com
Binomial Expansions 1 X N A B N N C 0 A N N C 1 A N 1 B N C 2 A
slideplayer.com
Example 14 Find The Rth Term From End In Expansion Of X A N
www.teachoo.com
How To Expand 1 X 3 In Series Quora
www.quora.com
Example 10 Find Term Independent Of X In 3 2 X 2 1 3x 6
www.teachoo.com
Example 6 Show That Middle Term In Expansion Of 1 X 2n Is
www.teachoo.com
The Binomial Series Binomial Series Expansions To The Power Series Graph
www.nabla.hr
How To Calculate The Binomial Expansion For 1 X N Quora
www.quora.com
Solved Problem 1 A Let F X N2 X N 0 Use The Negative Binomial Theorem To Find Integers C1 C2 C3 Such That F X C1 1 2 1 C2 1 X 2 Course Hero
www.coursehero.com
Example 14 Find The Rth Term From End In Expansion Of X A N
www.teachoo.com
Copyright C Cengage Learning All Rights Reserved Ppt Download
slideplayer.com
Binomial Theorem For Any Index A Plus Topper
www.aplustopper.com
Quadratic Formula Binomial Expansion Other Expansions Quadratic Formula Binomial Expansion Other Quadratics Quadratic Formula Mathematics Worksheets
www.pinterest.com
Solved Possibly Useful Formulas Binomial P X Nx Px 1 Chegg Com
www.chegg.com
Binomial Theorem
www.slideshare.net
Cbse Class 11 Maths Notes Binomial Theorem And Mathematical Induction Aglasem Schools
schools.aglasem.com
Ex 8 2 10 Coefficients Of R 1 R R 1 In 1 3 5
www.teachoo.com
Pascal S Triangle And The Binomial Theorem X Y 0 1 X Y 1 1x 1y X Y 2 1x 2 2xy 1y 2 X Y 3 1x 3 3x 2 Y 3xy 2 1 Y 3 X Ppt Download
slideplayer.com
Binomial Approximation Wikipedia
en.wikipedia.org
What Is The Binomial Expansion For 1 X 1 Quora
www.quora.com
The Binomial Theorem For A Negative And Fractional Index Youtube
www.youtube.com
What Is The Binomial Expansion For 1 X 1 Quora
www.quora.com
Tutorial 54 The Binomial Theorem
www.wtamu.edu
Binomial Theorem Study Material For Iit Jee Askiitians
www.askiitians.com
How Do We Expand Math Sqrt 1 X Math Using The Binomial Theorem Quora
www.quora.com
Solved 6 A Use The Binomial Formula And De Moivre S Fo Chegg Com
www.chegg.com
Phys208 Binomial Theorem
www.physics.udel.edu
Binomial Theorem
pt.slideshare.net
Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange
math.stackexchange.com
10 6 The Binomial Series
www.geocities.ws
Cbse Class 11 Maths Notes Binomial Theorem And Mathematical Induction Aglasem Schools
schools.aglasem.com
4 The Binomial Theorem
www.intmath.com
Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf
byjus.com
Binomial Approximation Wikipedia
en.wikipedia.org
Binomial Theorem
www.slideshare.net
Using The Binomial Theorem College Algebra
courses.lumenlearning.com
Ex 8 2 11 Prove That Coefficient Of Xn In 1 X 2n Ex 8 2
www.teachoo.com
Example 10 Find Term Independent Of X In 3 2 X 2 1 3x 6
www.teachoo.com
Mdm4u The Binomial Theorem Problem Solving
studylib.net
Binomial Theorem
www.slideshare.net
Solved Prove By The Mathematical Induction The Binomial E Chegg Com
www.chegg.com
Maths C4 Binomial Theorem Ppt Video Online Download
slideplayer.com
Binomial Theorem Wikipedia
en.wikipedia.org
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqzhtpanzd58y Idmp1vqv9xsa Dzqtzy8abads7qhkh9rvfoaz Usqp Cau
encrypted-tbn0.gstatic.com
Binomial Distribution Formula Knowledge Of Science By Shb Facebook
www.facebook.com
10 6 The Binomial Series
www.geocities.ws
If In The Expansion Of 1 X M 1 X N The Coefficients Of X And X 2 Are 3 And 6 Find Value Of M And N Mathematics Stack Exchange
math.stackexchange.com
The Binomial Expansion Ppt Download
slideplayer.com
6 Binomial Theorem Example 2 Finding The Term Independent Of X Youtube
www.youtube.com
Find The Coefficient Of 1 X In The Expansion Of 1 X N 1 X X N I F The Sum Of Binomial Coefficients Of The Expansion 2x 1 X N Is Equal To 256 Then Find Mathematics Topperlearning Com Chbwn8aa
www.topperlearning.com
Prove That The Coefficient Of The Middle Term In The Expansion Of 1 X 2n Is Equal To The Sum Of The Coefficient Of The Middle Term In The Expansion Of
www.topperlearning.com
Worksheet Pascal S Triangle And The Binomial Theorem Nagwa
www.nagwa.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcs L Uyi 9gvpcwaiwohes2sgn39k9yzlswwtop177dszwgz Ku Usqp Cau
encrypted-tbn0.gstatic.com
Binomial Theorem Preparation Tips Engineering
www.jagranjosh.com
Cbse Class 11 Maths Notes Binomial Theorem And Mathematical Induction Aglasem Schools
schools.aglasem.com
Phys208 Binomial Theorem
www.physics.udel.edu
Ex 8 2 10 Coefficients Of R 1 R R 1 In 1 3 5
www.teachoo.com
Binomial Theorem For Any Index
www.slideshare.net
Binomial Expansions 1 X N A B N N C 0 A N N C 1 A N 1 B N C 2 A
slideplayer.com
What Is The Binomial Expansion Of Math 1 X 2 Math Quora
www.quora.com
3
encrypted-tbn0.gstatic.com
Binomial Theorem Find Term Independent Of Variable X Youtube
www.youtube.com
If The First Three Terms In The Expansion Of 1 Ax N In The Ascending Power Of X Are 1 12x 64x 2 What Will Be A And N Quora
www.quora.com
Core 4 Binomial Expansion 1
www.slideshare.net
Extending The Binomial Theorem For Fractional Powers
studylib.net
Example 12 Show That Coefficient Of Middle Term In 1 X 2n Is
www.teachoo.com
The Coefficient Of X N In The Expansion Of 1 X 1 X N Is Youtube
www.youtube.com
Find Binomial Expansion Of Rational Functions
www.onlinemath4all.com
Example 6 Show That Middle Term In Expansion Of 1 X 2n Is
www.teachoo.com
Binomial Theorem Study Material For Iit Jee Askiitians
www.askiitians.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcrtbcsrju 6 Bwyczq8y6nyiwunrzonlofcpgfgavyc3yt8jjpk Usqp Cau
encrypted-tbn0.gstatic.com
Binomial Expansions 1 X N A B N N C 0 A N N C 1 A N 1 B N C 2 A
slideplayer.com
Using The Binomial Theorem College Algebra
courses.lumenlearning.com
10 6 The Binomial Series
www.geocities.ws
3 6 The Binomial And Multinomial Theorems
mathonweb.com
Binomial Expansion And Series A Level Maths Uptuition With Mr Will
uptuition.id
Factorials To Binomial Theorem
www.mathsmutt.co.uk
General And Middle Term Binomial Theorem Formula Videos Examples
www.toppr.com
Binomial Expansion Formula For 1 Plus X Whole Power N
www.onlinemath4all.com
Solved Compute The Following Binomial Probabilities Direc Chegg Com
www.chegg.com
Cbse Class 11 Maths Notes Binomial Theorem And Mathematical Induction Aglasem Schools
schools.aglasem.com
Solved A Let F X Zn N 0 Use The Negative Binomial Chegg Com
www.chegg.com
Example 12 Show That Coefficient Of Middle Term In 1 X 2n Is
www.teachoo.com
What Is The Expansion Of Math 1 X 1 Math Quora
www.quora.com
Show That The Middle Term In The Expansion X 1 X 2n I S 1 3 5 2n 1 N 2 N Youtube
www.youtube.com
Binomial Theorem
www.slideshare.net
Binomial Theorem For Any Index
www.slideshare.net
Find Binomial Expansion Of Rational Functions
www.onlinemath4all.com
Expanding A Bx N When N Is Negative Using The Binomial Theorem Youtube
www.youtube.com
Maclaurin S Series
www.mathsmutt.co.uk
9 5 The Binomial Theorem
studylib.net
Binomial Expansions 1 X N A B N N C 0 A N N C 1 A N 1 B N C 2 A
slideplayer.com
Binomial Theorem For Any Index A Plus Topper
www.aplustopper.com
Binomial Theorem Wikipedia
en.wikipedia.org
