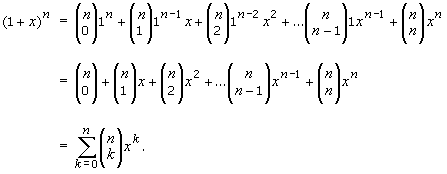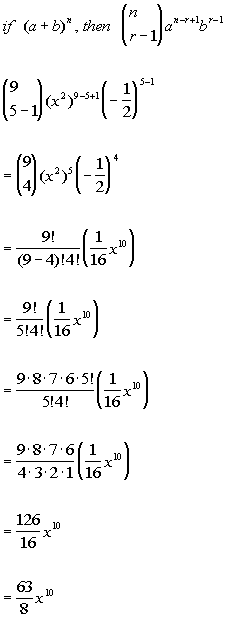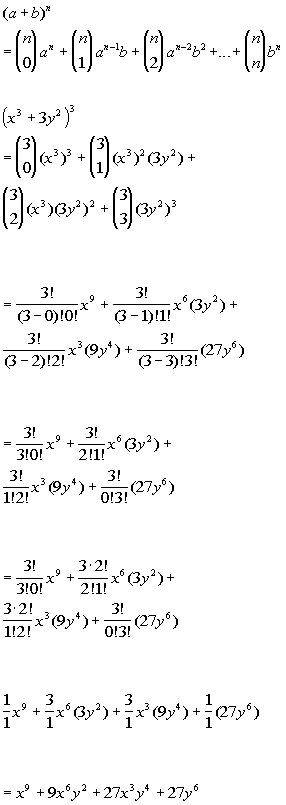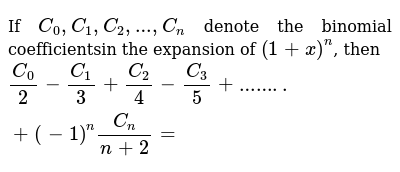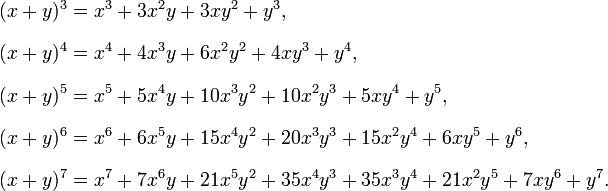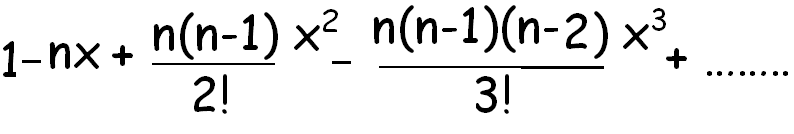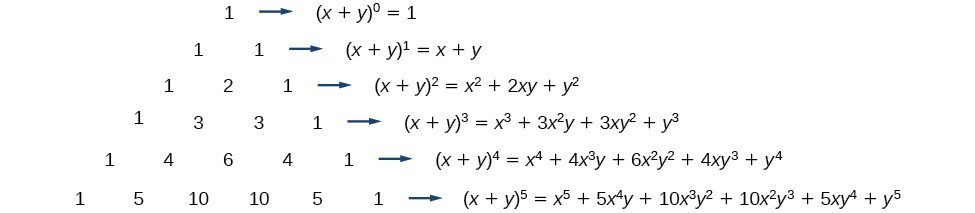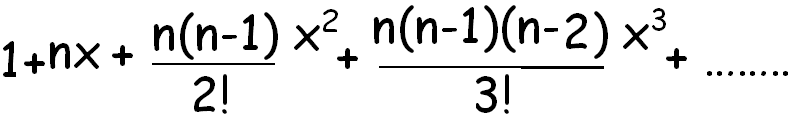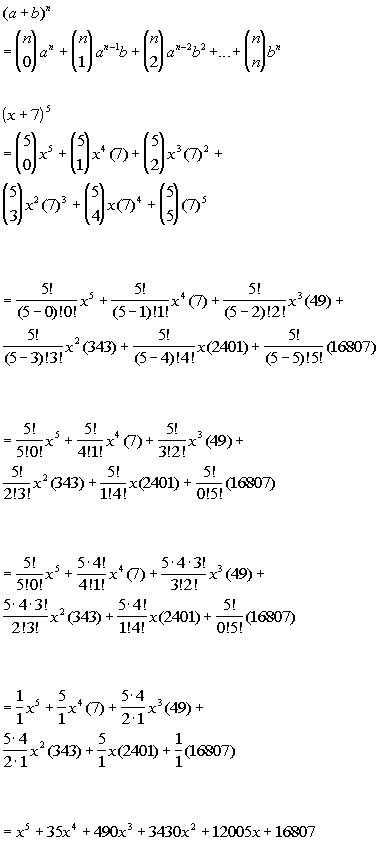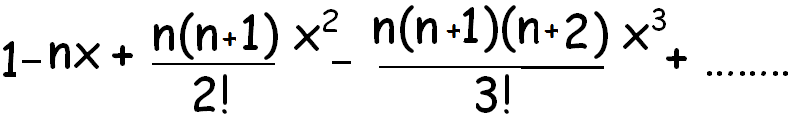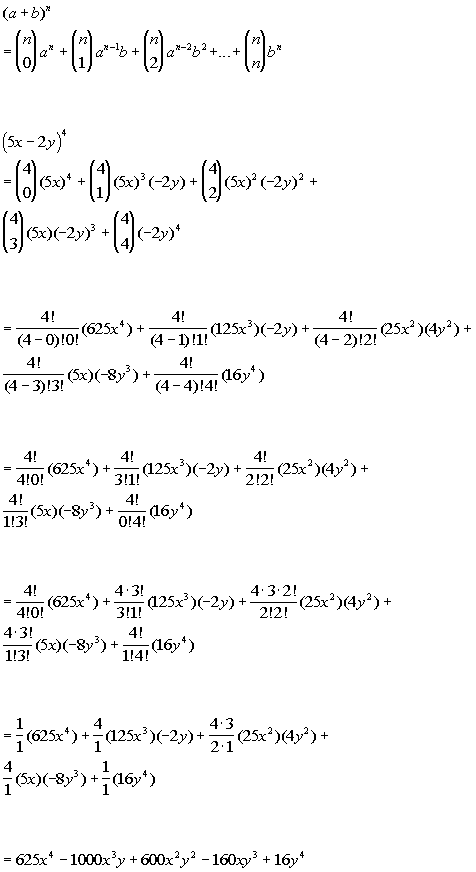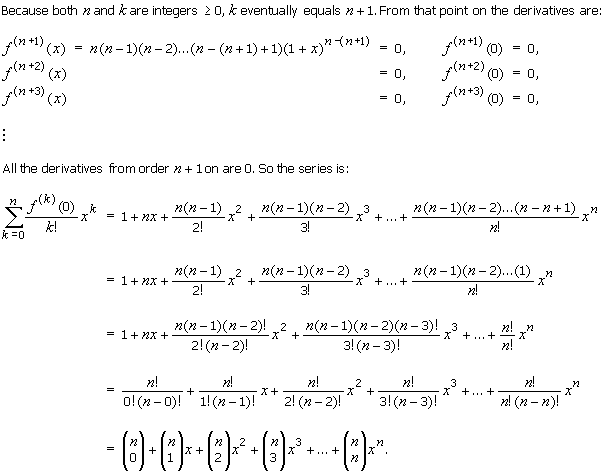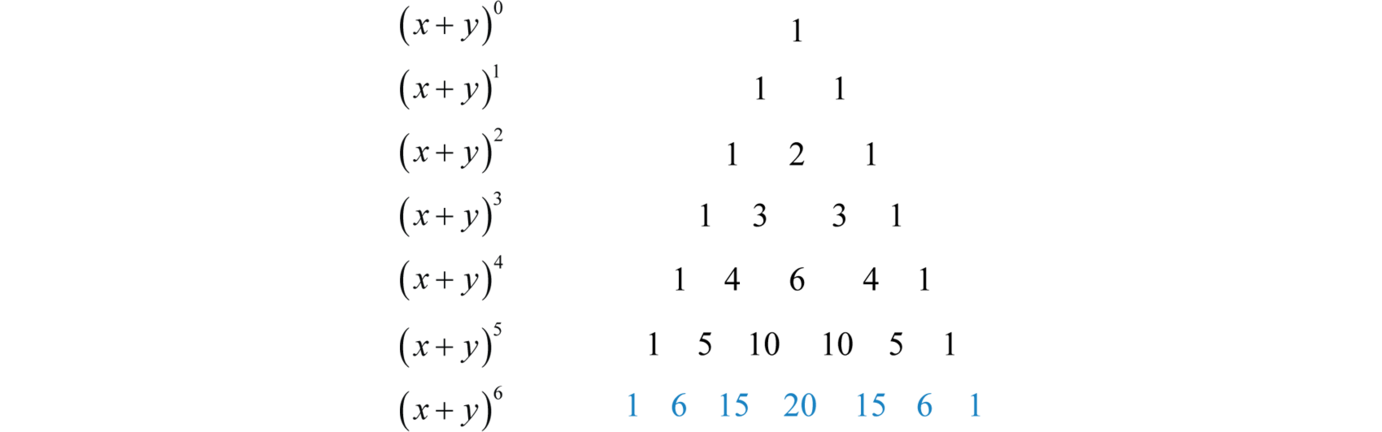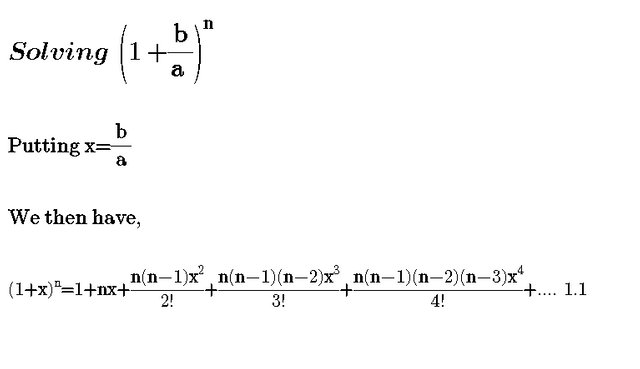Binomial Expansion Formula 1xn
Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf
byjus.com
Binomial Expansions 1 X N A B N N C 0 A N N C 1 A N 1 B N C 2 A
slideplayer.com
Use The Binomial Theorem To Prove The Formula For The Derivative Of X N Stumbling Robot
www.stumblingrobot.com
A Level Maths Binomial Expansion The Student Room
www.thestudentroom.co.uk
Solved Prove By The Mathematical Induction The Binomial E Chegg Com
www.chegg.com
Extending The Binomial Theorem For Fractional Powers
studylib.net
1 1n n it gets more accurate the higher the value of n that formula is a binomial right.
Binomial expansion formula 1xn. Here we are going to see the formula for the b inomial expansion formula for 1 plus x whole power n. The binomial theorem states that where n is a positive integer. In elementary algebra the binomial theorem or binomial expansion describes the algebraic expansion of powers of a binomialaccording to the theorem it is possible to expand the polynomial x y n into a sum involving terms of the form ax b y c where the exponents b and c are nonnegative integers with b c n and the coefficient a of each term is a specific positive integer depending.
We can write down the binomial expansion of 1xn as 1dfracn1x dfracnn 12x2 dfracnn 1n 23x3 this is true for all real. So lets use the binomial theorem. Here it represents the product of all the whole.
Xynsumk0n n choose k xn k yk also recall that the factorial notation n. Binomial expansion formula for 1 plus x whole power n. First we can drop 1 n k as it is always equal to 1.
In mathematics the binomial coefficients are the positive integers that occur as coefficients in the binomial theoremcommonly a binomial coefficient is indexed by a pair of integers n k 0 and is written. Binomial expansion formula for 1 plus x whole power n. The expression of the binomial theorem formula is given as follows.
This means use the binomial theorem to expand the terms in the brackets but only go as high as x 3. 2 x 4 2 4 1 x2 4 can be expanded by binomial theorem since. It is the coefficient of the x k term in the polynomial expansion of the binomial power 1 x n and it is given by the formula for example the fourth power of 1 x is.
A b n a n n c 1a n 1 b n c 2a n 2 b 2 n c n 1ab n 1 b n. And quite magically most of what is left goes to 1 as n goes to infinity.
Find The Coefficient Of 1 X In The Expansion Of 1 X N 1 X X N I F The Sum Of Binomial Coefficients Of The Expansion 2x 1 X N Is Equal To 256 Then Find Mathematics Topperlearning Com Chbwn8aa
www.topperlearning.com
Example 6 Show That Middle Term In Expansion Of 1 X 2n Is
www.teachoo.com
General And Middle Term Binomial Theorem Formula Videos Examples
www.toppr.com
The Binomial Expansion Ppt Download
slideplayer.com
What Is The Binomial Expansion For 1 X 1 Quora
www.quora.com
10 6 The Binomial Series
www.geocities.ws
10 6 The Binomial Series
www.geocities.ws
Cbse Class 11 Maths Notes Binomial Theorem And Mathematical Induction Aglasem Schools
schools.aglasem.com
Binomial Theorem
www.slideshare.net
Extending The Binomial Theorem For Fractional Powers
studylib.net
9 5 The Binomial Theorem
studylib.net
Tutorial 54 The Binomial Theorem
www.wtamu.edu
Binomial Theorem Wikipedia
en.wikipedia.org
Download Binomial Theorem Mathematics Allen Kota Study Material For
www.slideshare.net
6 Binomial Theorem Example 2 Finding The Term Independent Of X Youtube
www.youtube.com
Binomial Theorem For Any Index A Plus Topper
www.aplustopper.com
The Binomial Series Binomial Series Expansions To The Power Series Graph
www.nabla.hr
Example 12 Show That Coefficient Of Middle Term In 1 X 2n Is
www.teachoo.com
Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange
math.stackexchange.com
Binomial Approximation Wikipedia
en.wikipedia.org
Binomial Theorem For Any Index
www.slideshare.net
Binomial Expansion And Series A Level Maths Uptuition With Mr Will
uptuition.id
Tutorial 54 The Binomial Theorem
www.wtamu.edu
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqzhtpanzd58y Idmp1vqv9xsa Dzqtzy8abads7qhkh9rvfoaz Usqp Cau
encrypted-tbn0.gstatic.com
If C 0 C 1 C 2 C N Denote The Binomial Coefficientsin Th
doubtnut.com
Given That The Binomial Expansion Is 1 X 100 How Does One Deduce That 104 10 19804 By Substituting A Suitable Value Of X In The Binomial Expansion Quora
www.quora.com
Example 10 Find Term Independent Of X In 3 2 X 2 1 3x 6
www.teachoo.com
How To Expand 1 X 3 In Series Quora
www.quora.com
Binomial Theorem For Any Index
www.slideshare.net
Phys208 Binomial Theorem
www.physics.udel.edu
How To Calculate The Binomial Expansion For 1 X N Quora
www.quora.com
Binomial Theorem
www.slideshare.net
The Binomial Theorem Extension 1 Content Ppt Download
slideplayer.com
01 Binomial Theorem Combinatorics Numbers
www.scribd.com
Expand 1 X X 2 4 Using Binomial Expansion Youtube
www.youtube.com
Core 4 Binomial Expansion 1
www.slideshare.net
Example 6 Show That Middle Term In Expansion Of 1 X 2n Is
www.teachoo.com
Example 8 The 2nd 3rd 4th Terms In Expansion X A N Are 240
www.teachoo.com
Ex 8 2 10 Coefficients Of R 1 R R 1 In 1 3 5
www.teachoo.com
Cbse Class 11 Maths Notes Binomial Theorem And Mathematical Induction Aglasem Schools
schools.aglasem.com
Binomial Theorem Abstract Algebra Combinatorics
www.scribd.com
Example 12 Show That Coefficient Of Middle Term In 1 X 2n Is
www.teachoo.com
If In The Expansion Of 1 X M 1 X N The Coefficients Of X And X 2 Are 3 And 6 Find Value Of M And N Mathematics Stack Exchange
math.stackexchange.com
What Is The Binomial Expansion Of Math 1 X 2 Math Quora
www.quora.com
Maclaurin S Series
www.mathsmutt.co.uk
Binomial
www.slideshare.net
Binomial Theorem Maths Help
sites.google.com
Find Binomial Expansion Of Rational Functions
www.onlinemath4all.com
Chapter 18 Binomial Theorem Rd Sharma Solutions For Class 11 Science Mathematics Cbse Topperlearning
www.topperlearning.com
Quadratic Formula Binomial Expansion Other Expansions Quadratic Formula Binomial Expansion Other Quadratics Quadratic Formula Mathematics Worksheets
www.pinterest.com.mx
Binomial Theorem Preparation Tips Engineering
www.jagranjosh.com
Using The Binomial Theorem College Algebra
courses.lumenlearning.com
Example 14 Find The Rth Term From End In Expansion Of X A N
www.teachoo.com
Using The Binomial Theorem College Algebra
courses.lumenlearning.com
Http Www Math For All Grades Com Mathglossary Html
Find Binomial Expansion Of Rational Functions
www.onlinemath4all.com
Ex 8 2 10 Coefficients Of R 1 R R 1 In 1 3 5
www.teachoo.com
Pascal S Triangle Wikipedia
en.wikipedia.org
Tutorial 54 The Binomial Theorem
www.wtamu.edu
Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange
math.stackexchange.com
Binomial Expansions 1 X N A B N N C 0 A N N C 1 A N 1 B N C 2 A
slideplayer.com
Maths C4 Binomial Theorem Ppt Video Online Download
slideplayer.com
Alg2 March28 The Answers
studylib.net
What Is The Binomial Expansion For 1 X 1 Quora
www.quora.com
Buy Quadratic Formula Binomial Expansion Other Expansions Quadratic Formula Binomial Expansion Oth Quadratics Quadratic Formula Learning Mathematics
www.pinterest.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcrtxkptmqwumkkxbhtbd1lixemmf Kfshif8ntvca9bfz3yxfe0 Usqp Cau
encrypted-tbn0.gstatic.com
Binomial Theorem Study Material For Iit Jee Askiitians
www.askiitians.com
Binomial Theorem
pt.slideshare.net
Find Binomial Expansion Of Rational Functions
www.onlinemath4all.com
Binomial Theorem Wikipedia
en.wikipedia.org
Binomial Expansions 1 X N A B N N C 0 A N N C 1 A N 1 B N C 2 A
slideplayer.com
Example 14 Find The Rth Term From End In Expansion Of X A N
www.teachoo.com
Cbse Class 11 Maths Notes Binomial Theorem And Mathematical Induction Aglasem Schools
schools.aglasem.com
Binomial Theorem For Any Index A Plus Topper
www.aplustopper.com
Solved Use The Binomial Series To Find The Maclaurin Seri Chegg Com
www.chegg.com
How Do We Expand Math Sqrt 1 X Math Using The Binomial Theorem Quora
www.quora.com
Binomial Expansions 1 X N A B N N C 0 A N N C 1 A N 1 B N C 2 A
slideplayer.com
Factorials To Binomial Theorem
www.mathsmutt.co.uk
3 6 The Binomial And Multinomial Theorems
mathonweb.com
Tutorial 54 The Binomial Theorem
www.wtamu.edu
10 6 The Binomial Series
www.geocities.ws
Binomial Theorem
saylordotorg.github.io
Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf
byjus.com
Ncr Formula
Binomial Theorem Use Of Complex Numbers In Binomial Theorem Sum
doubtnut.com
10 6 The Binomial Series
www.geocities.ws
The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium
medium.com
Binomial Theorem Applications Examples Study Com
study.com
Binomial Theorem Study Material For Iit Jee Askiitians
www.askiitians.com
Binomial Approximation Wikipedia
en.wikipedia.org
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcrtxkptmqwumkkxbhtbd1lixemmf Kfshif8ntvca9bfz3yxfe0 Usqp Cau
encrypted-tbn0.gstatic.com
Deriving Of Binomial Expansion Formula For Two Variables A B N Steemit
steemit.com
Example 6 Show That Middle Term In Expansion Of 1 X 2n Is
www.teachoo.com
Pure Mathematics And Mechanics The Binomial Theorem
pure-maths.blogspot.com
What Is The Expansion Of Math 1 X 1 Math Quora
www.quora.com
If The Constant Term In The Binomial Expansion Of X 2 1 X N N
doubtnut.com
Prove That The Coefficient Of The Middle Term In The Expansion Of 1 X 2n Is Equal To The Sum Of The Coefficient Of The Middle Term In The Expansion Of
www.topperlearning.com
If The First Three Terms In The Expansion Of 1 Ax N In The Ascending Power Of X Are 1 12x 64x 2 What Will Be A And N Quora
www.quora.com
