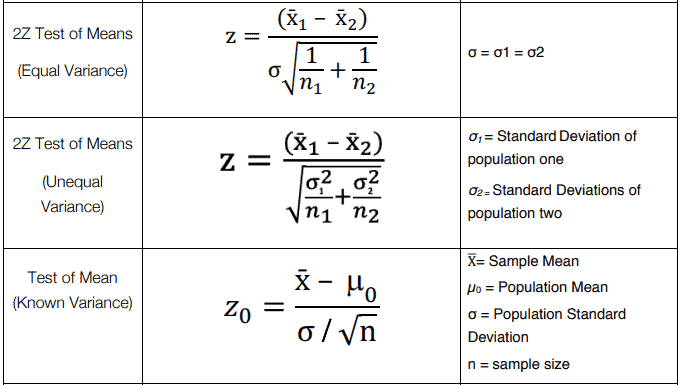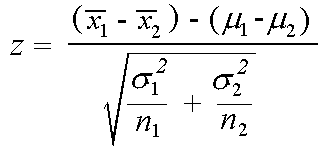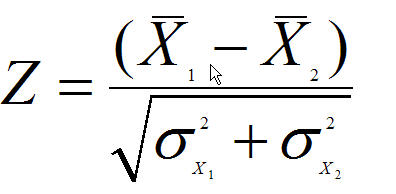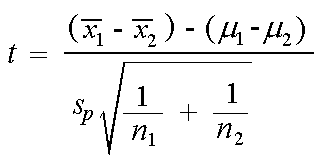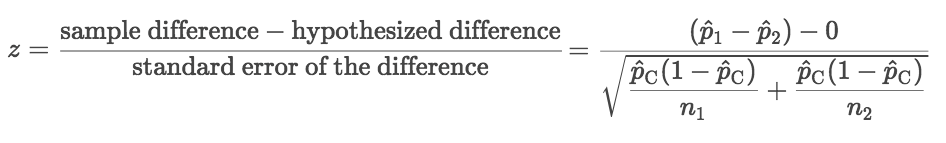Z Test Formula For Two Sample Mean
Two normally distributed but independent populations s is known formula.
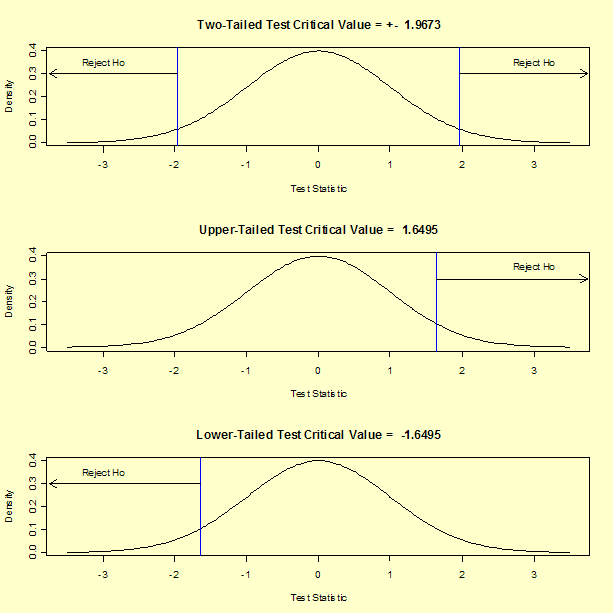
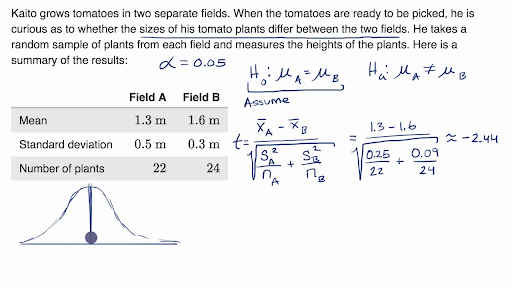
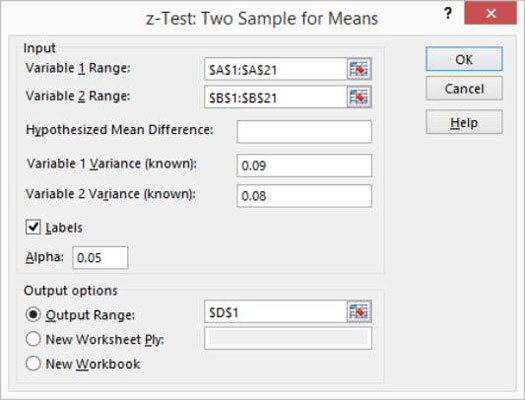
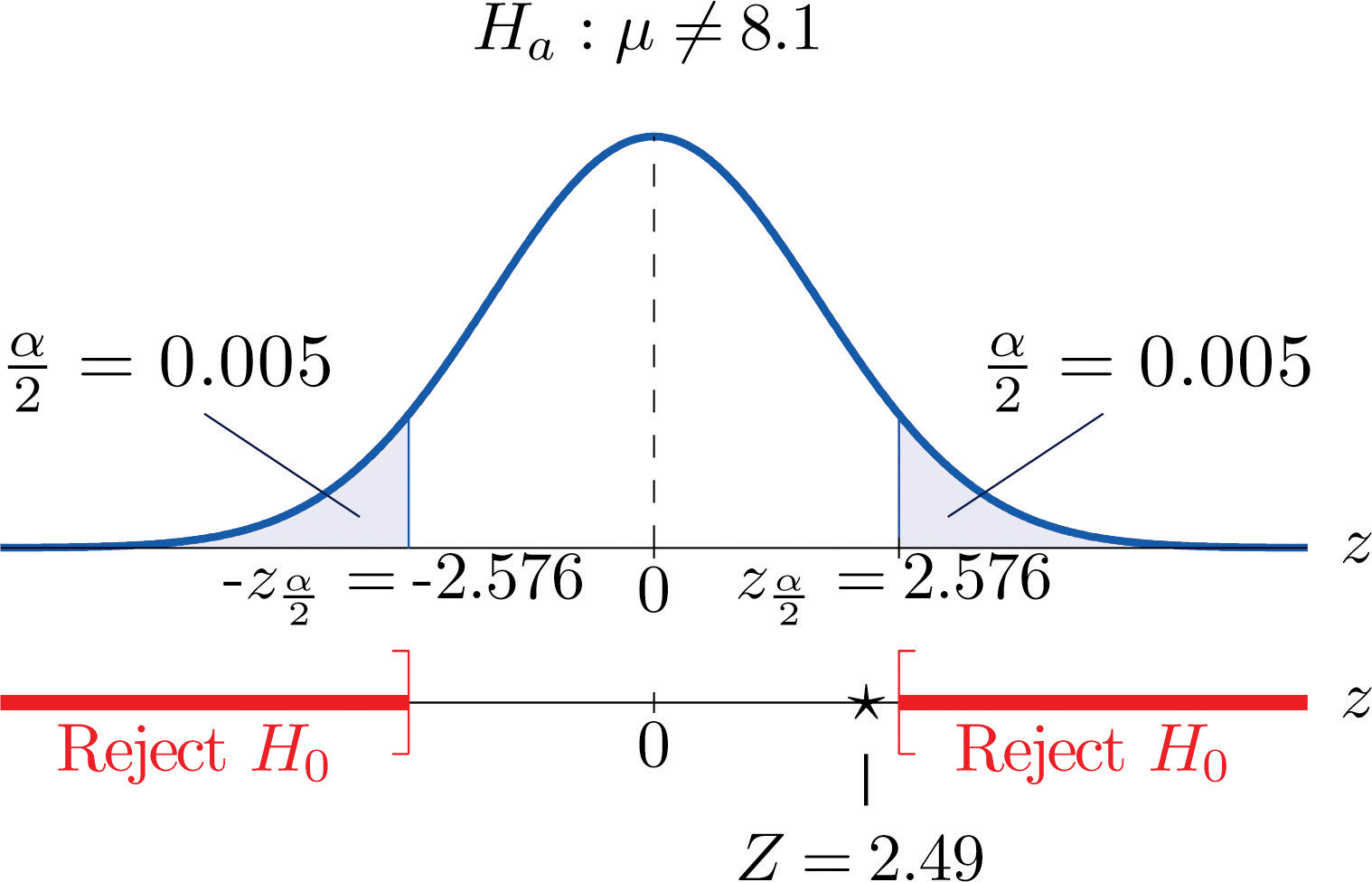
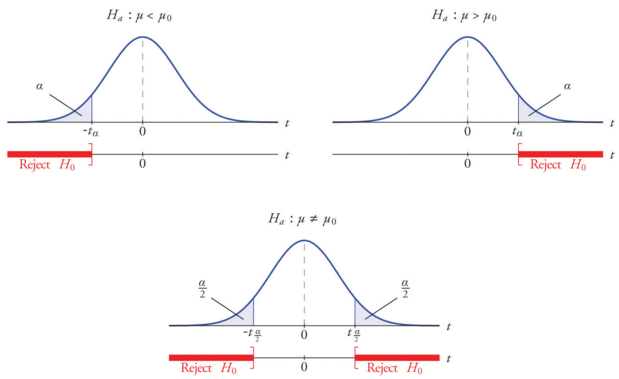
Z test formula for two sample mean. To see how ztest can be used in a formula to compute a two tailed probability value see the remarks section below. Firstly calculate the sample mean and sample standard deviation. The rejection regions for three posssible alternative hypotheses using our example data are shown below.
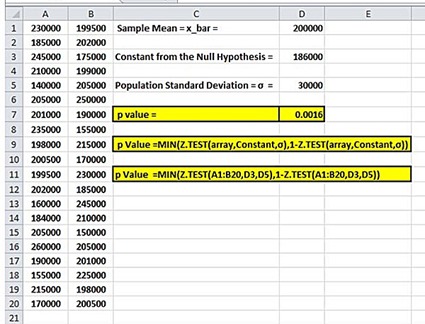
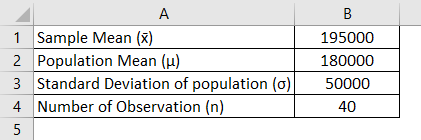
For a given hypothesized population mean x ztest returns the probability that the sample mean would be greater than the average of observations in the data set array that is the observed sample mean. A herd of 1500 steer was fed a special highprotein grain for a month. Where h1 is called an alternative hypothesis the mean of two populations is not equal.
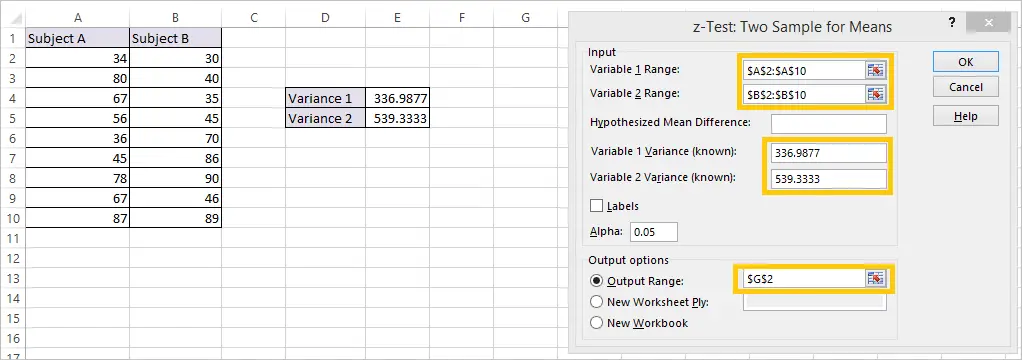
The z test for two means. In that case he can use a z test statistics method to obtain the results by taking a sample size say 500 from the city out of which suppose 280 are tea drinkers. Look up the significance level of the zvalue in the standard normal table table in appendix b.
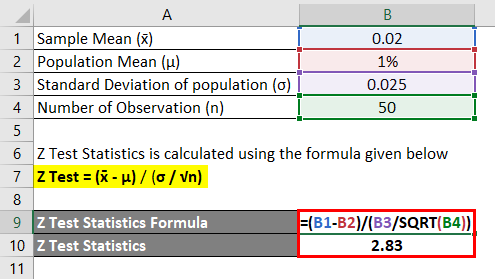
U 1 u 2 0. Z x m o the formula for z test statistics for a sample is derived by using the following steps. Z test tests the mean of a distribution.
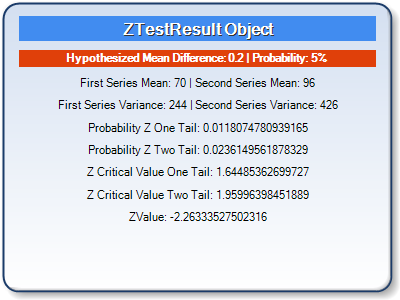
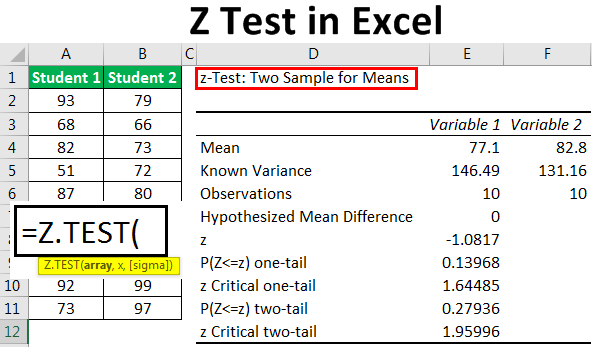
While using the z test we test a null hypothesis which states that the mean of the two population is equal. More about the z test for two means so you can better use the results delivered by this solver. Z test for two samples requirements.
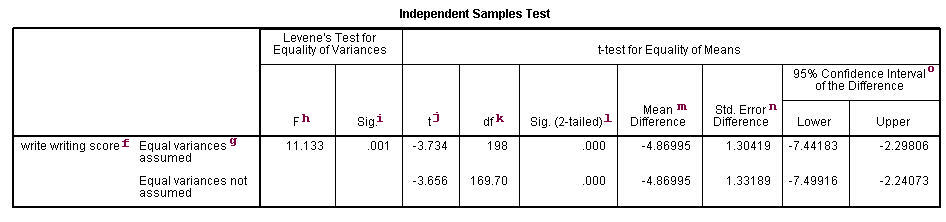
Finally the z test statistics is computed by deducting population mean from the variable and then the result is divided by the population standard deviation as shown below. Lets take an example to understand the usage of two sample z test. More specifically we are interested in assessing whether or not it is reasonable to claim that the two population means the population means.
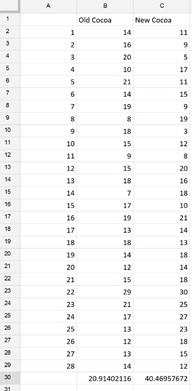
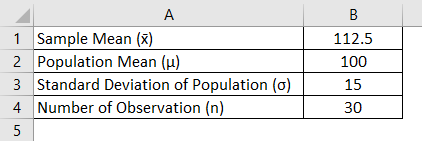
Z test statistics formula example 1. Population standard deviation step 2. A random sample of 29 were weighed and had gained an.
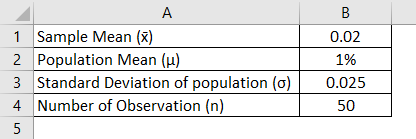
U 1 u 2 0. The amount of a certain trace element in blood is known to vary with a standard deviation of 141 ppm parts per. Where is the sample mean d is a specified value to be tested s is the population standard deviation and n is the size of the sample.
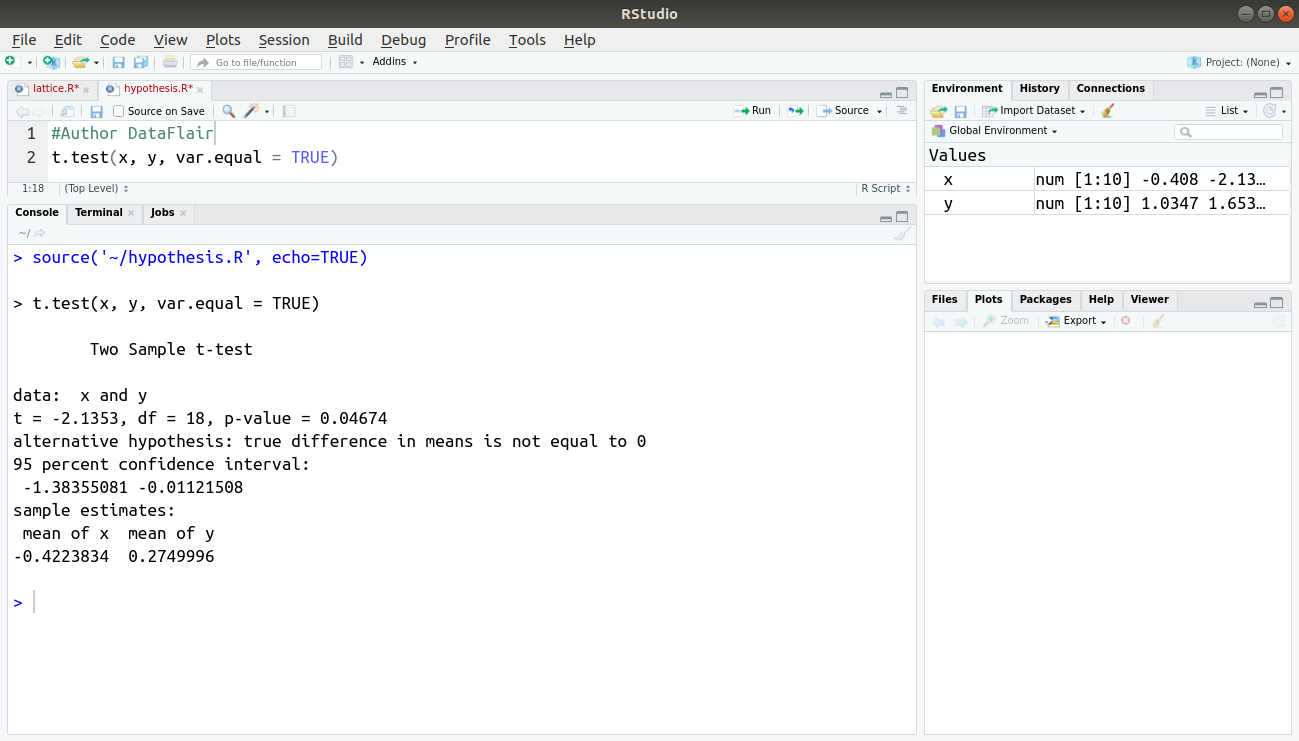
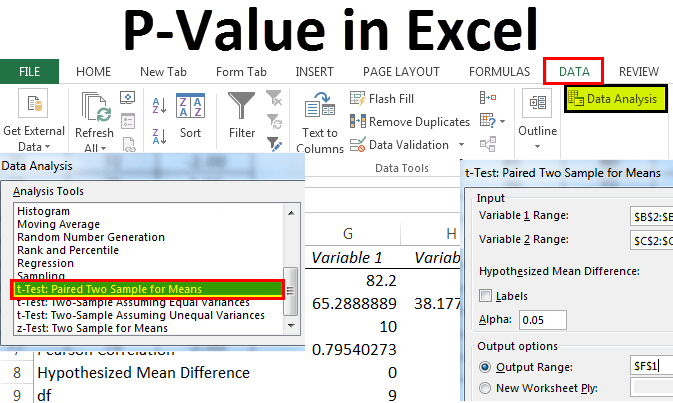
For our two tailed t test the critical value is t 1 a2n 19673 where a 005 and n 326. Where and are the means of the two samples d is the hypothesized difference between the population means 0 if testing for equal means s 1 and s 2 are the standard deviations of the two populations and n 1 and n 2 are the sizes of the two samples. Two sample z test.
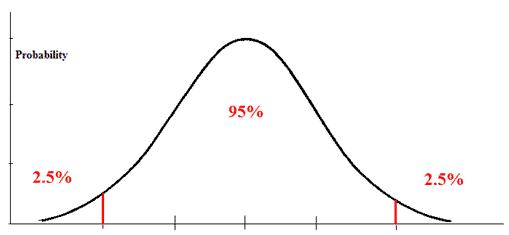
For each significance level in the confidence interval the z test has a single critical value for example 196 for 5 two tailed which makes it more convenient than the students t test whose critical values are defined by the sample size through the corresponding degrees of freedom. Suppose a person wants to check or test if tea and coffee both are equally popular in the city.













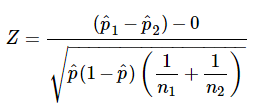

:max_bytes(150000):strip_icc()/Clipboard01-5c94e6b446e0fb00010ae8ed.jpg)
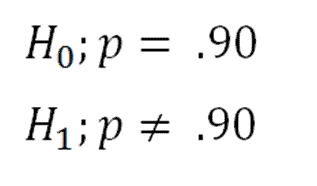


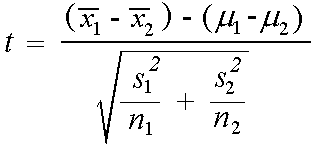







/comparing-two-proportions-57b5a4e33df78cd39c67380b.jpg)





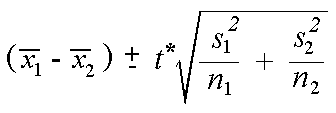








/ttest22-0afd4aefe9cc42628f603dc2c7c5f69a.png)