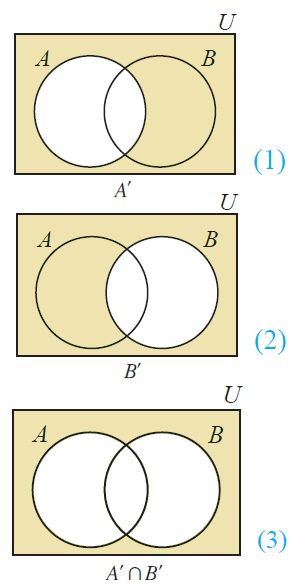
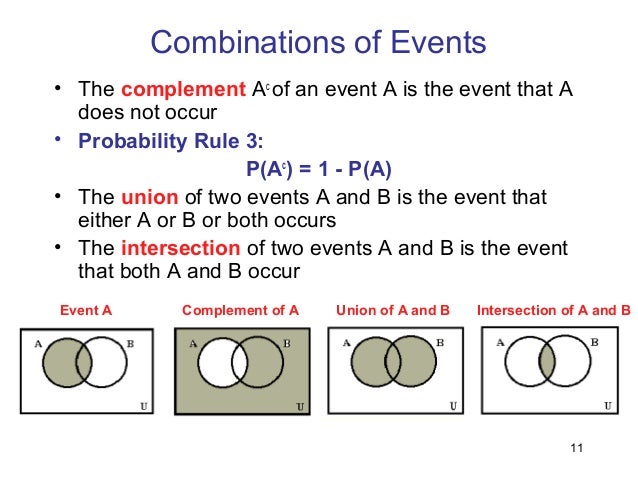
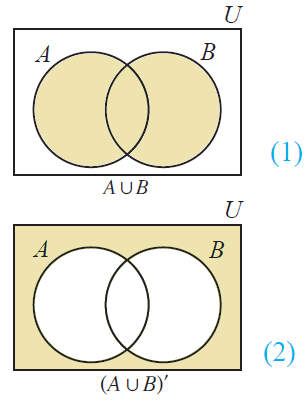
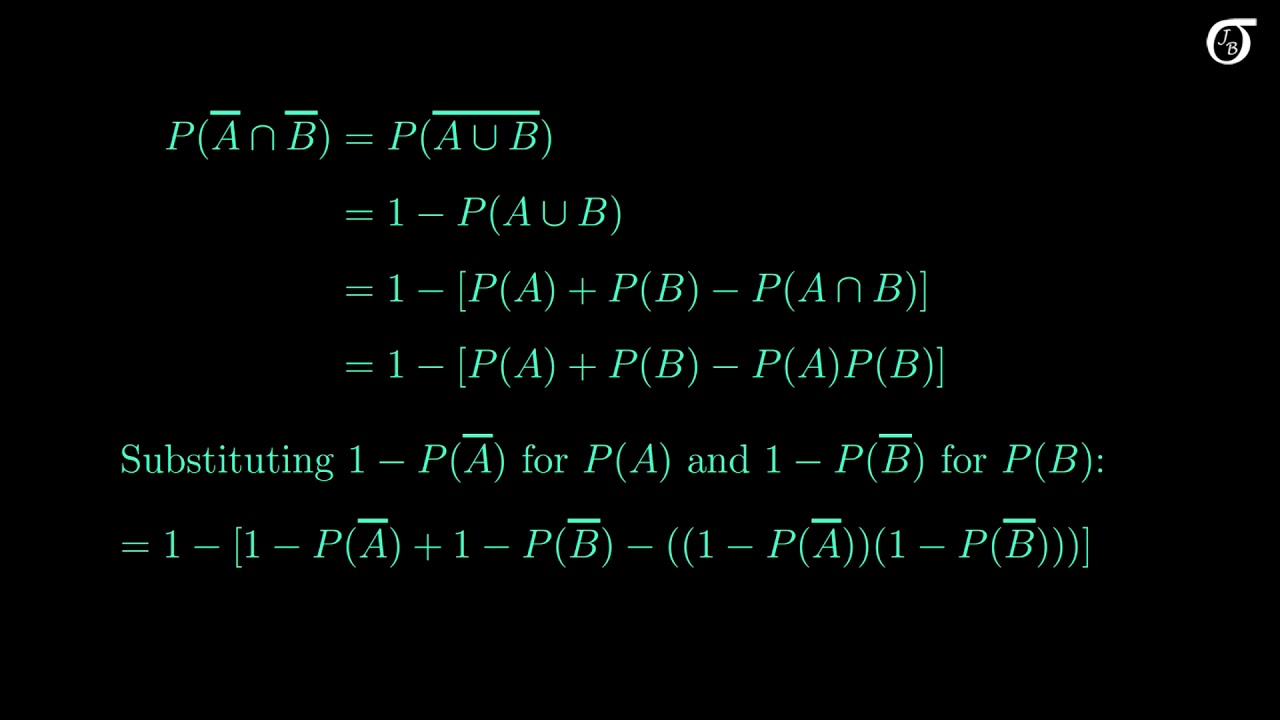Pa Complement Union B Complement Formula
.
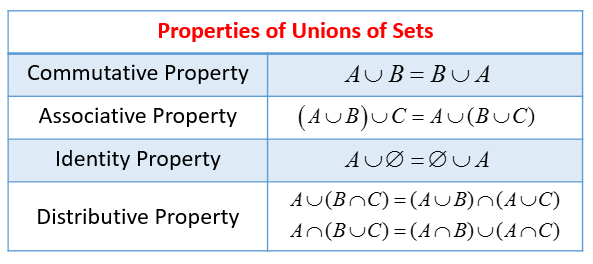
Pa complement union b complement formula. Examples. Pa b pa pb pa b the next example in which we compute the probability of a union both by counting and by using the formula shows why the last term in the formula is needed. Pacup b pa pb pacap b the next example in which we compute the probability of a union both by counting and by using the formula shows why the last term in the formula is needed.
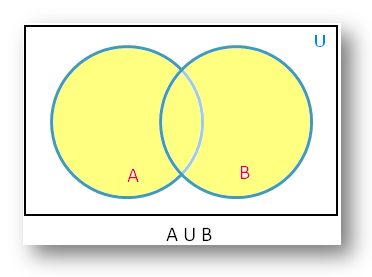
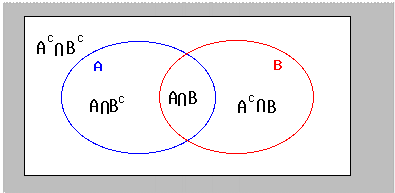
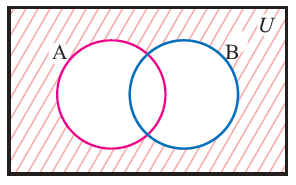
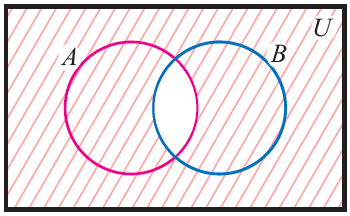
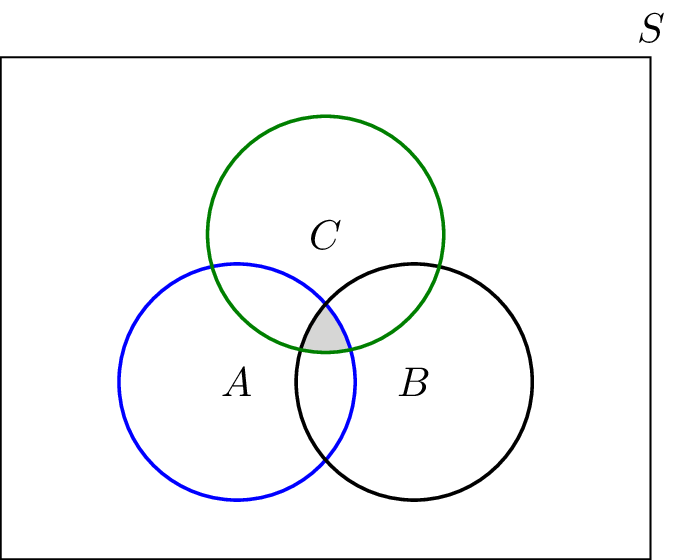
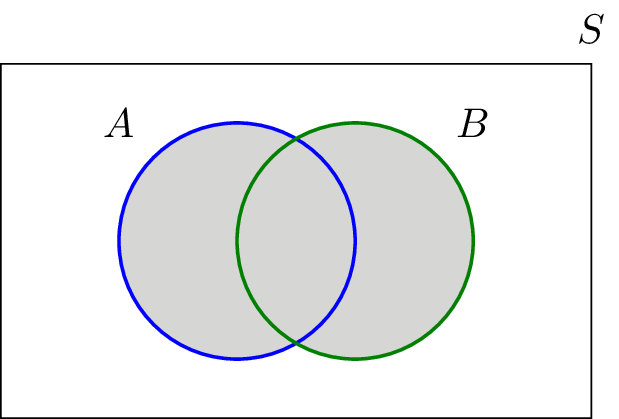
Venn diagram of a u b. The relative complement of a in b is denoted b a according to the iso 31 11 standardit is sometimes written b a but this notation is ambiguous as in some contexts it can be interpreted as the set of all elements b a where b is taken from b and a from a. Example 17 two fair dice are thrown.
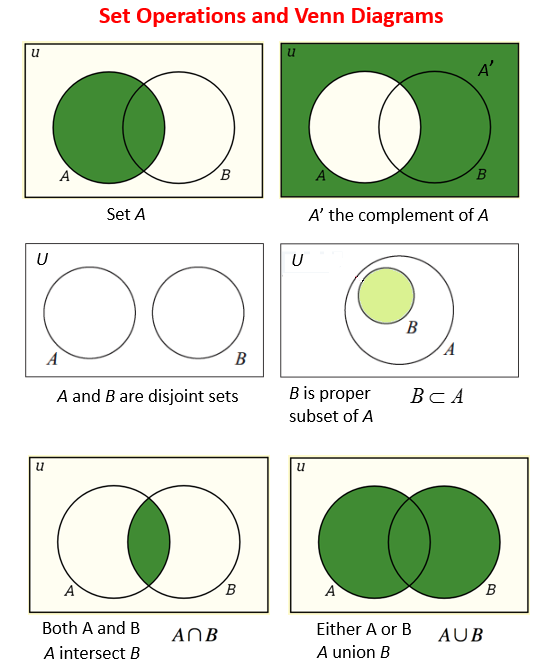
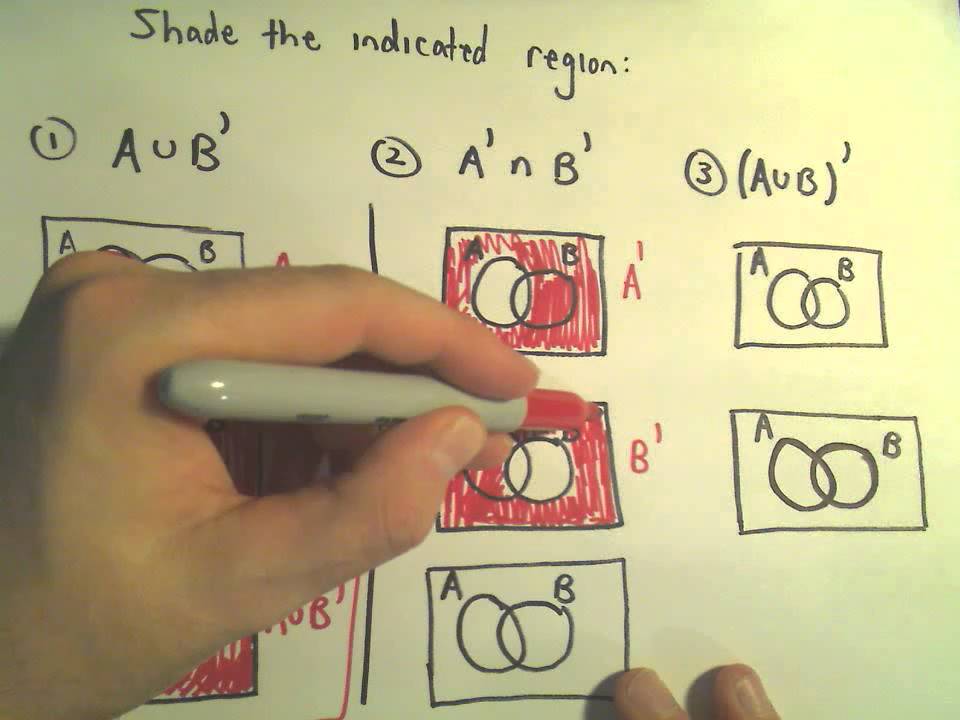
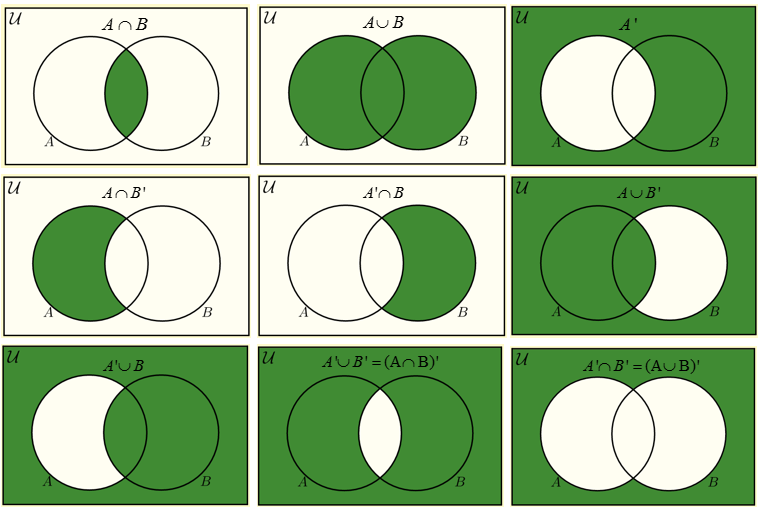
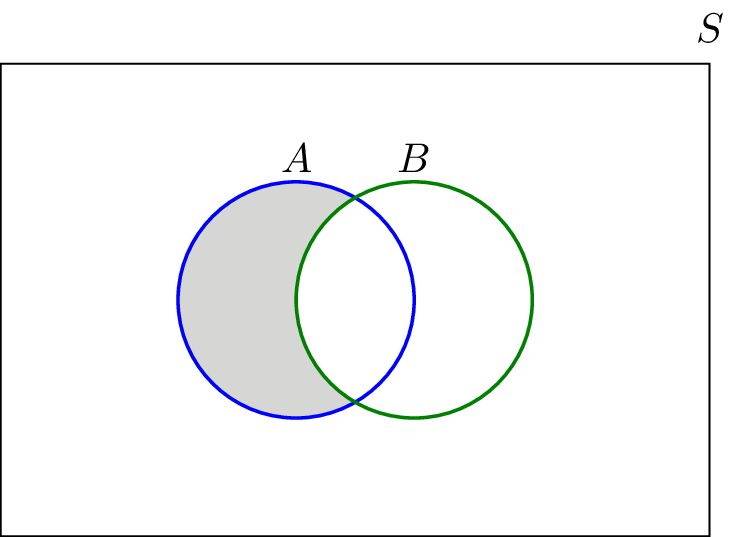
This concept introduces the student to complements in particular finding the probability of events by using the complement rule. You might also see mutually exclusive for sets that have no intersection. First draw venn diagram for a u b and then a u b.
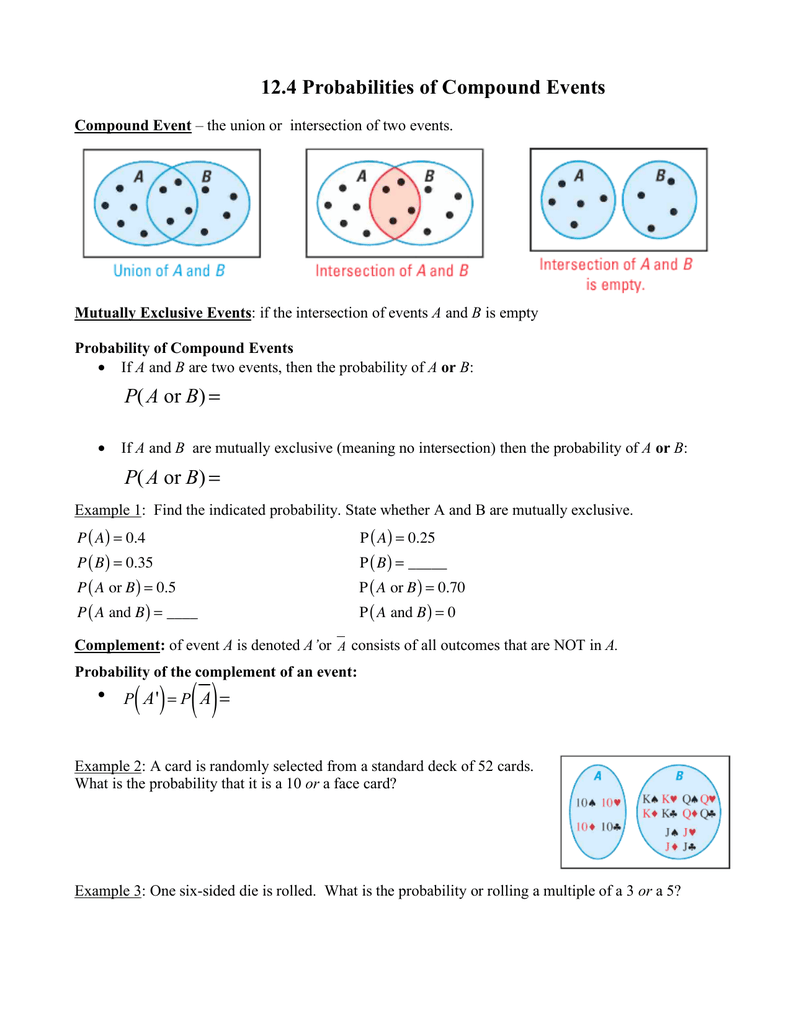
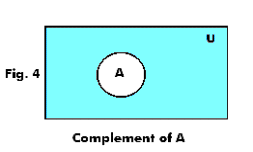
If events a and b are mutually exclusive pa b 0. How to prove the complement rule in probability. To represent a u b in venn diagram we have to shade the region other than a and b.
Let a represent the set of all males in a class and b represent the set of all females. The conditional probability of event a given event b is denoted by the symbol pab. Addition rules in probability.
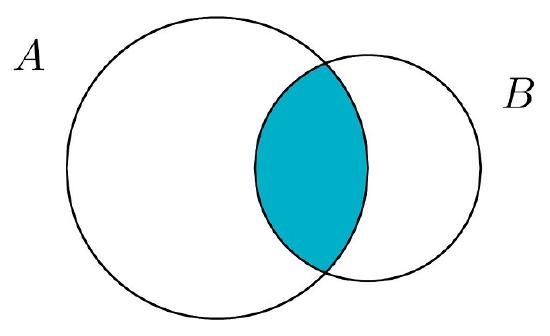
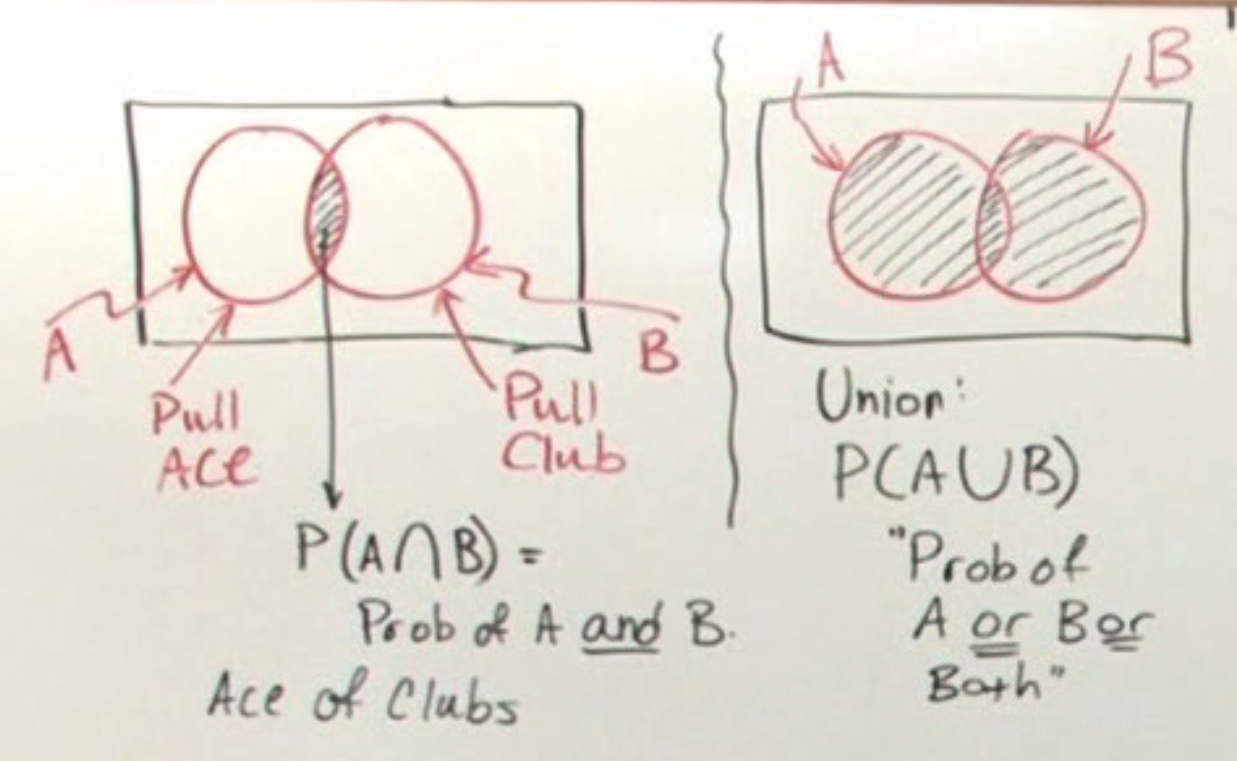
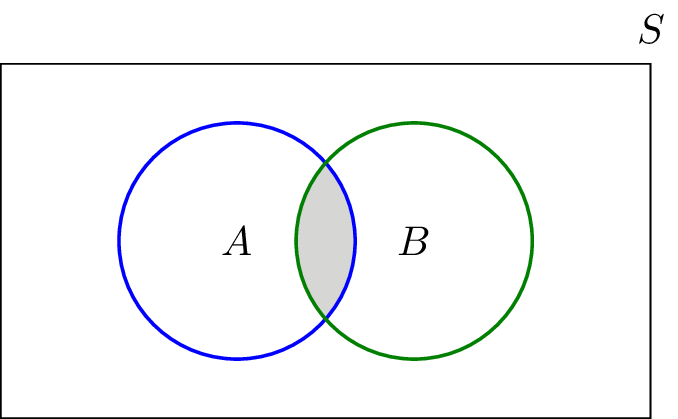
Pab papb pab pab papb if ab is empty. The probability that events a and b both occur is the probability of the intersection of a and b. If is the set of real numbers and is the set of.
Formula for union of 3 sets. The probability of the intersection of events a and b is denoted by pa b. The probability that event a will notoccur is denoted by pa.
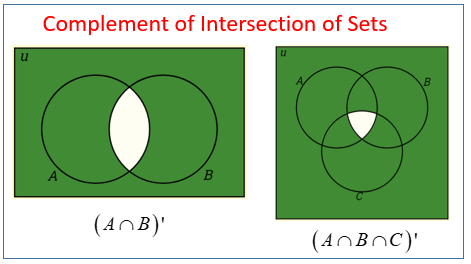
The complement of an event is the event not occuring. The probability of the union of events a and b is denoted by pa b. The probability that events a or b occur is the probability of the union of a and b.






/conditional-56edf9de5f9b5867a1c1924c.jpg)


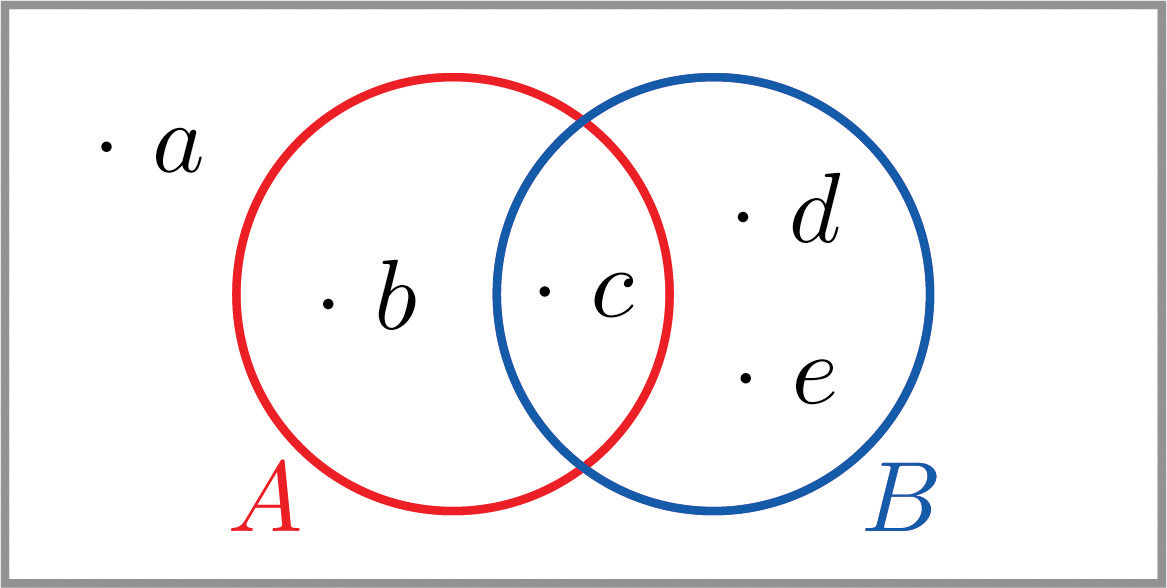



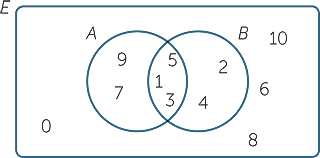
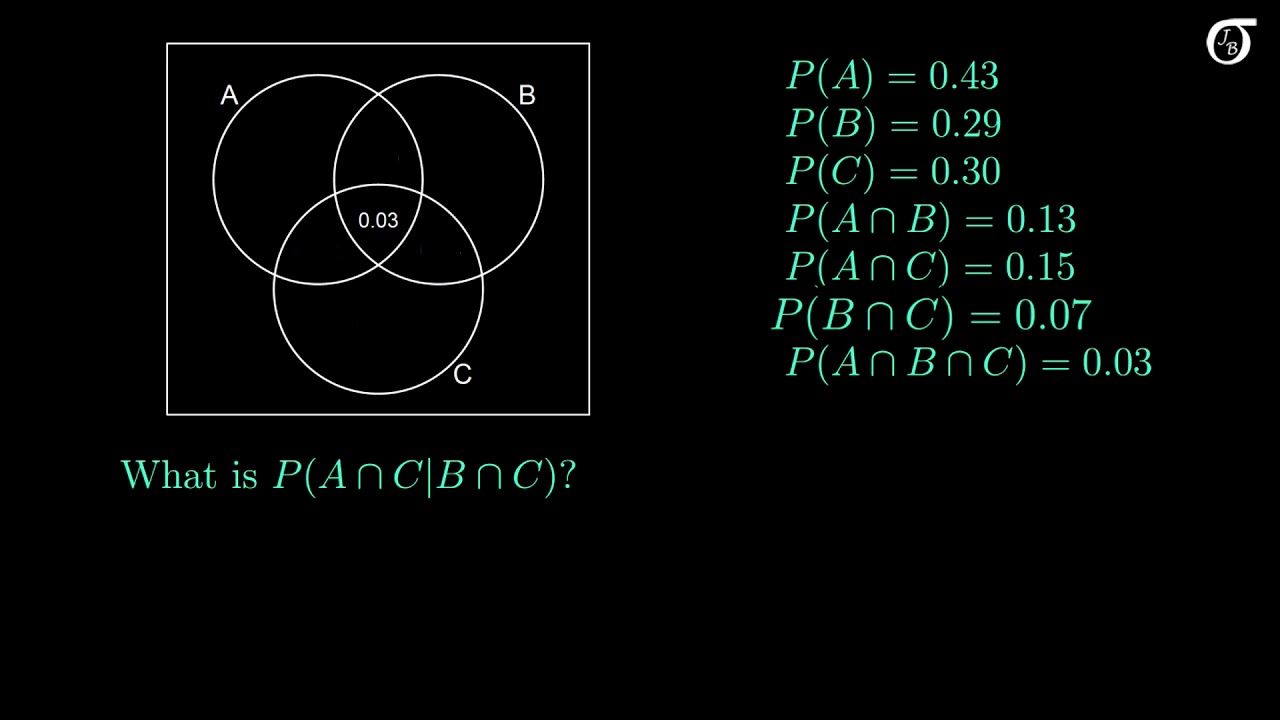





/complement-56a8fa9a5f9b58b7d0f6e9e7.jpg)


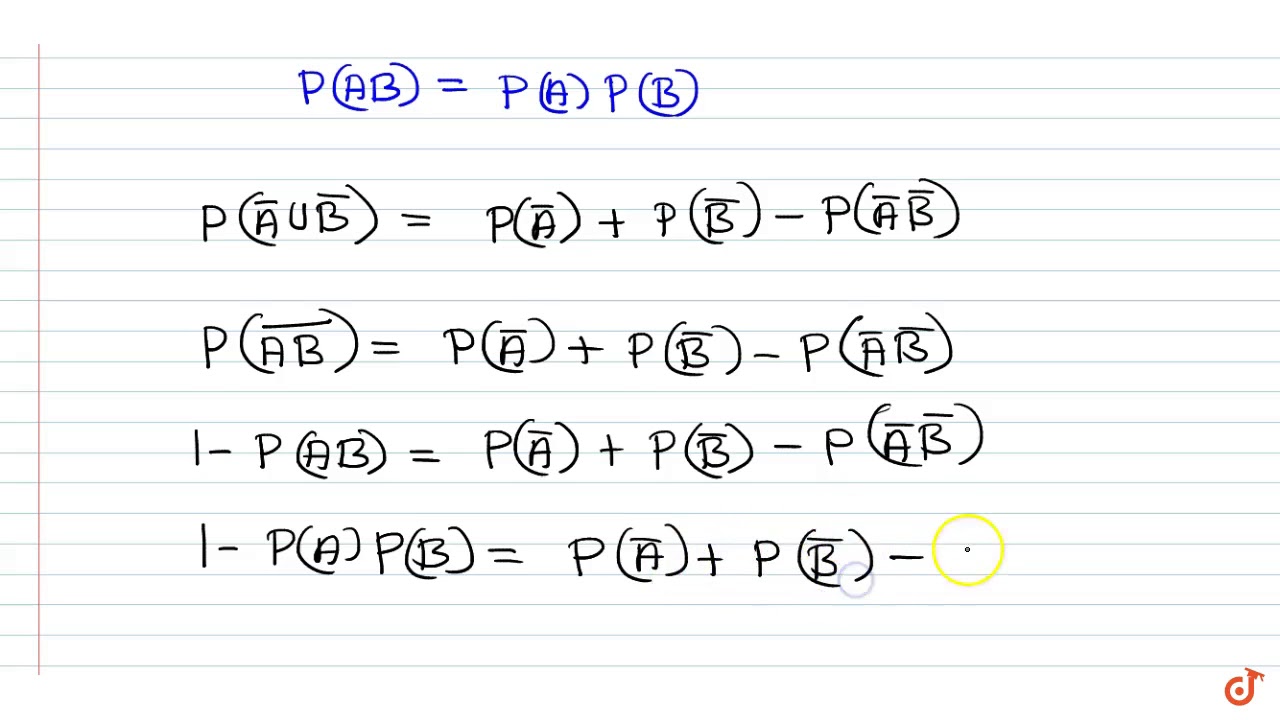



/complement-56a8fa9a5f9b58b7d0f6e9e7.jpg)



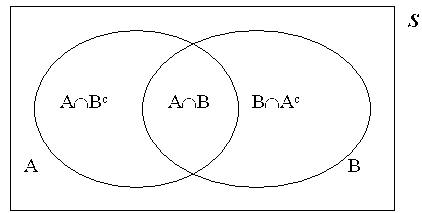


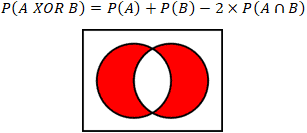








/addition-57bc15a75f9b58cdfdf894b7.jpg)

/complement-56a8fa9a5f9b58b7d0f6e9e7.jpg)