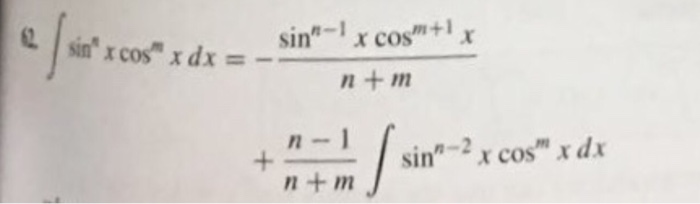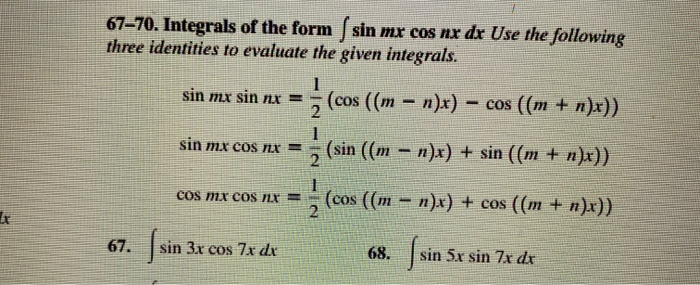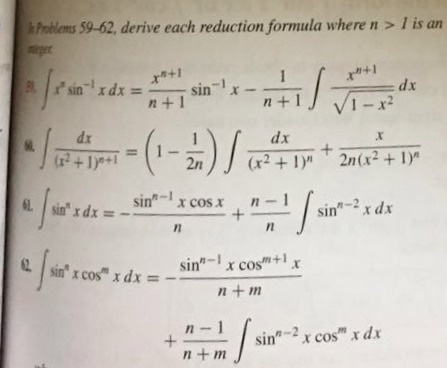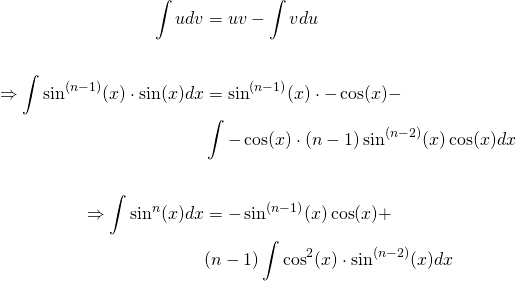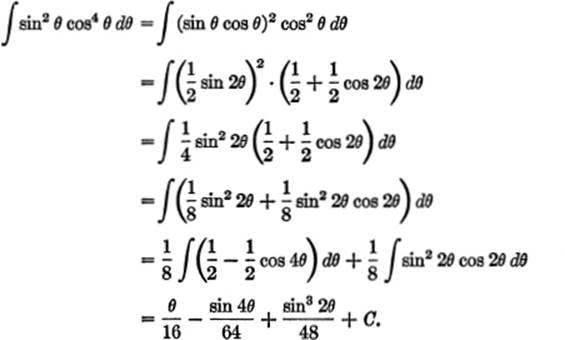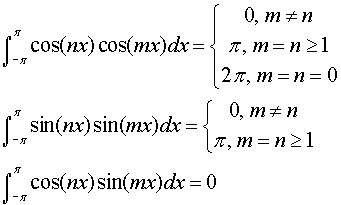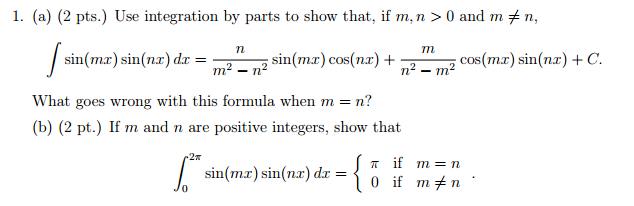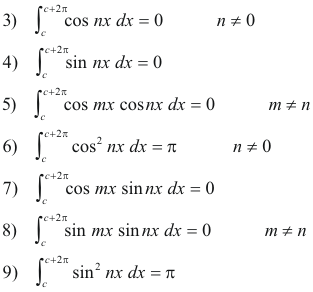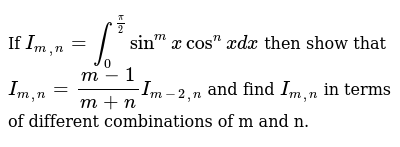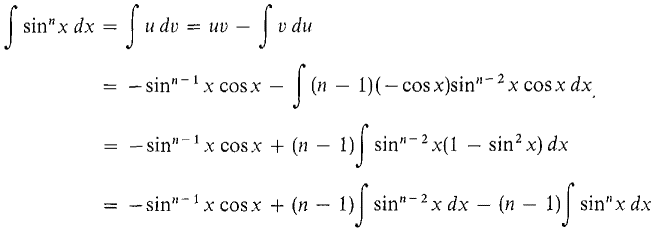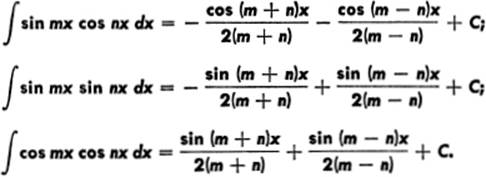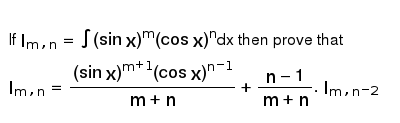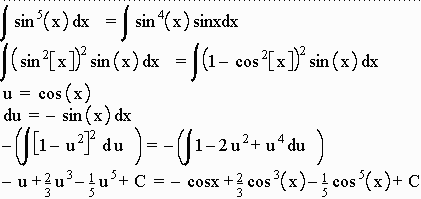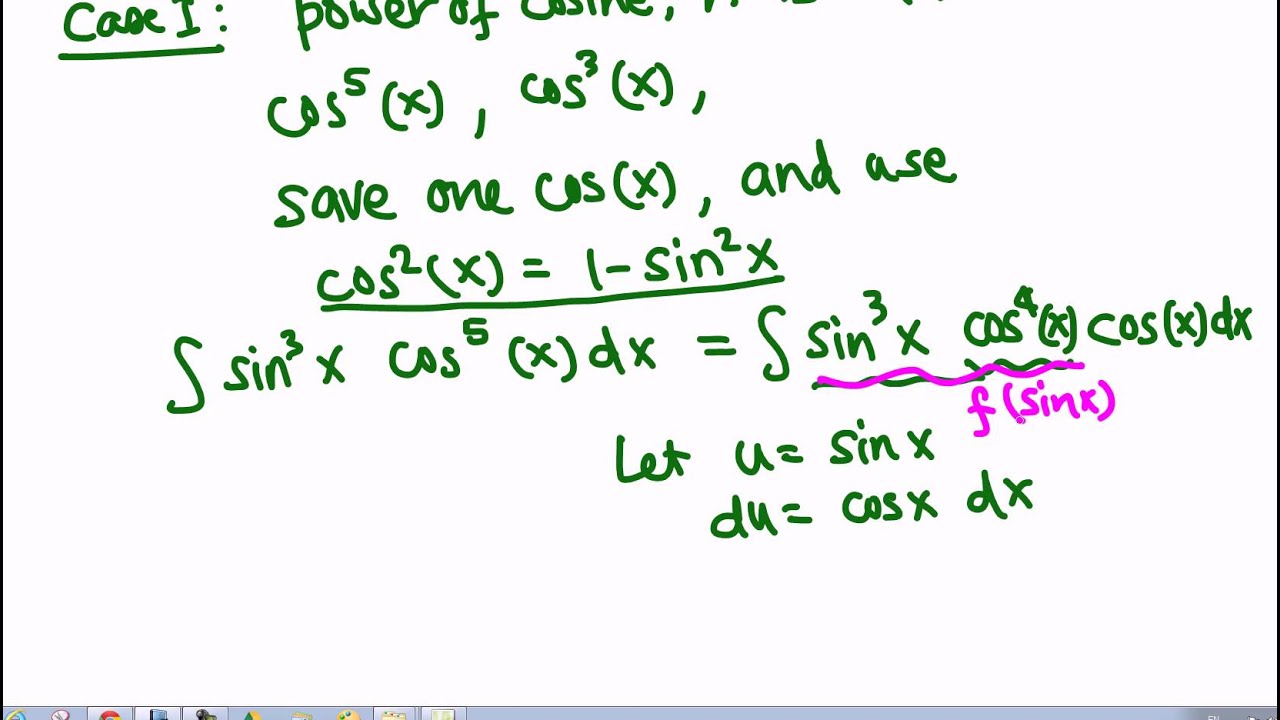Integral Sinm X Cosn X Dx Formula
2
Pdf On The Wallis Formula
www.researchgate.net
Answered What Substitutions Are Made To Evaluate Bartleby
www.bartleby.com
Mixture Reduction Formula For Sinx M Cosx N With Limits 0 To Pi 2
keral2008.blogspot.com
Trigonometric Integrals
studylib.net
Prove The Orthogonality Relations For Sine And Cosine Stumbling Robot
www.stumblingrobot.com
Integrals of the form int sinm xcosn x dx in learning the technique of substitution we saw the integral int sin xcos x dx in example 614.
Integral sinm x cosn x dx formula. Then use the change of variable u sinx. The reduction formula can be derived using any of the common methods of integration like integration by substitution integration by parts integration by trigonometric substitution integration by partial fractions etcthe main idea is to express an integral involving an integer parameter eg. We start by using double angle formulas z sin2xcos4xdx z secxcosx2 cos2xdx z 1 4 sin22xcos2xdx 1 8 z sin22x1cos2xdx 1 16 z 1 cos4x1cos2xdx 1 16 z 6 1 cos4xcos2x cos4xcos2xdx and using 4 we we can compute.
As an application of the previous example we compute the integral z sin2xcos4xdx. The integration was not difficult and one could easily evaluate the indefinite integral by letting usin x or by letting u cos x. Reduction formula of sinmxcosnx reduction formula for sinmx cosnx reduction formula of sinnxcosmx.
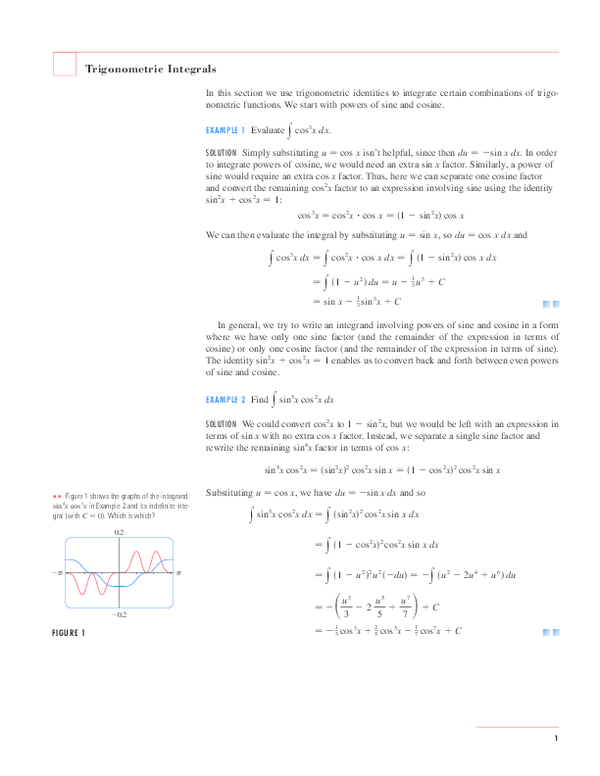
Power of a function represented by i n in terms of an. Solution we could evaluate this integral using the reduction formula for equation 567 together with example 3 as in exercise 33 in section 56 but a better. 598 integration techniques if the exponent of cosine is odd split off one cosx and use the identity cos2x 1 sin2x to rewrite the remaining even power of cosine in terms of sine.
Example z tanxdx lnjsecxjc proof z tanxdx sinx cosx dx using the substitution u cosx we get du sinx giving us that the above integral is. Reduction formula is very useful in solving integration problem. Powers of tangent can be reduced using the formula tan2 x sec2 x 1 example z tan0 xdx z 1dx xc.
Integration Of A Product Of Sin M X Cos N X Youtube
www.youtube.com
Give Reduction Formula For Cos M X Sin Nx Dx Sarthaks Econnect Largest Online Education Community
www.sarthaks.com
Mathematics Notes
www.learnpick.in
Solved Use The Reduction Formula In Example 6 To Show Tha Chegg Com
www.chegg.com
Integrate The Integral Cos Mx Cos Nx Dx M N Sarthaks Econnect Largest Online Education Community
www.sarthaks.com
Integration By Reduction Formulae Wikipedia
en.wikipedia.org
13 Evaluate S Sin 5x Cos X Dx Also Prove That 52 Sin Mx Cos Nx Homeworklib
www.homeworklib.com
2
Https Ocw Mit Edu Resources Res 18 008 Calculus Revisited Complex Variables Differential Equations And Linear Algebra Fall 2011 Study Materials Mitres 18 008 Partiii Sol08 Pdf
Https Ocw Mit Edu Resources Res 18 008 Calculus Revisited Complex Variables Differential Equations And Linear Algebra Fall 2011 Study Materials Mitres 18 008 Partiii Sol08 Pdf
Solved Derive Each Reduction Formula Where N 1 Is An In Chegg Com
www.chegg.com
Solved 50 53 Reduction Formulas Use Integration By Parts Chegg Com
www.chegg.com
Solved In Problems 59 62 Derive Each Reduction Formula W Chegg Com
www.chegg.com
Reduction Formula For Integral Of Sin N X Dx Steemit
steemit.com
Reduction Formula Basic Concepts Reducing Sin Nx Cos Nx Reducing Sin Nx Cos Nx Youtube
www.youtube.com
Difficult Integrals Important Fur Fourier Series Physics Forums
www.physicsforums.com
List Of Definite Integrals Wikipedia
en.wikipedia.org
Https Ocw Mit Edu Resources Res 18 008 Calculus Revisited Complex Variables Differential Equations And Linear Algebra Fall 2011 Study Materials Mitres 18 008 Partiii Sol08 Pdf
Problems About Integration By Parts
www.yumpu.com
2
2
Trigonometric Integrals Special Methods Of Integration The Calculus Primer
schoolbag.info
Y Cos 3 X Dx Y Cos 2 X Cos X Dx Y 1 Sin 2 X Cos X Dx Y 1 U 2 Du U 1 3u 3 C Pdf Free Download
docplayer.net
What Is The Reduction Formula Of The Integration Of Sin Nx Dx From Limit 0 To Pi 2 Quora
www.quora.com
1
encrypted-tbn0.gstatic.com
Fjax0113 P5 Trigonometric Functions Real Analysis
www.scribd.com
2
2
Https Ocw Mit Edu Resources Res 18 008 Calculus Revisited Complex Variables Differential Equations And Linear Algebra Fall 2011 Study Materials Mitres 18 008 Partiii Sol08 Pdf
Give Reduction Formula For Sin Mx Cos Nx Dx Sarthaks Econnect Largest Online Education Community
www.sarthaks.com
Introduction To Integral Calculus E D U C A T I O N
www.ibusciencecollege.com
Integration Calculus Notes
www.learnpick.in
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqrb 4299di0robmy 6n3fm Ndoakece9so89 Hlu9oyujikett Usqp Cau
encrypted-tbn0.gstatic.com
Fourier 3
www.slideshare.net
Copyright C Cengage Learning All Rights Reserved 7 Techniques Of Integration Ppt Download
slideplayer.com
Prove The Orthogonality Relations For Sine And Cosine Stumbling Robot
www.stumblingrobot.com
Solved Please Show All Your Work To Receive Full Credit Chegg Com
www.chegg.com
8 3 Trigonometric Integrals
studylib.net
7 Techniques Of Integration 7 2 Trigonometric Integrals Techniques Of Integration In This Section We Will Learn How To Use Trigonometric Identities Ppt Download
slideplayer.com
Homework Math 414 502 Narcowich
www.math.tamu.edu
Fourier Series 1
www.slideshare.net
Pdf Fourier Series Ceyhan Yoney Academia Edu
www.academia.edu
Definite Integral Of Sin 2 X Cos 2 X Youtube
www.youtube.com
2
Solved Use Integration By Parts To Show That If M N 0 Chegg Com
www.chegg.com
7 2 Trigonometric Integrals Ppt Download
slideplayer.com
Integration Calculus Notes
www.learnpick.in
Derivation Of Formulas
solitaryroad.com
Trigonometric Integrals Bruce E Shapiro
www.yumpu.com
Reduction Formula 04 Reduction Formula For Sin Mx Cos Nx Maths World Youtube
www.youtube.com
Calculus 2 Integration Of Trig Fcts 16 Of 16 Integral Of Sin M X Cos N X General Approach Youtube
www.youtube.com
If I M N Int 0 Pi 2 Sin Mx Cos Nx Dx Then Show That I
doubtnut.com
Answered 77 Let M N Be Integers With M N Bartleby
www.bartleby.com
Https Ocw Mit Edu Resources Res 18 008 Calculus Revisited Complex Variables Differential Equations And Linear Algebra Fall 2011 Study Materials Mitres 18 008 Partiii Sol08 Pdf
Easy And Fun Trig Integrals
studylib.net
Https Ocw Mit Edu Resources Res 18 008 Calculus Revisited Complex Variables Differential Equations And Linear Algebra Fall 2011 Study Materials Mitres 18 008 Partiii Sol08 Pdf
Https Ocw Mit Edu Resources Res 18 008 Calculus Revisited Complex Variables Differential Equations And Linear Algebra Fall 2011 Study Materials Mitres 18 008 Partiii Sol08 Pdf
Fourier Series
www.slideshare.net
Solution Ncssm
www.yumpu.com
Calculus 2 How Do You Integrate 87 Of 300 Find The Integral Of Sin Mx Cos Nx Dx Youtube
www.youtube.com
Solved 6 Points Find The Fourier Sine Sine Series Of F Chegg Com
www.chegg.com
Use The Following Three Identities To Evaluate The Given Integrals Sin M X Sin N X Frac 1 2 Cos M N
www.slader.com
Use The Following Three Identities To Evaluate The Given Integrals Sin M X Sin N X Frac 1 2 Cos M N
www.slader.com
Integration Shortcut Integration Sin Mx Cos Nx Dx Both M N Are Odd Concept Youtube
www.youtube.com
2
Solved These Problems Ask You To Show That The Definite I Chegg Com
www.chegg.com
2
Solved A In Class We Noticed That Integrals Of The Form Chegg Com
www.chegg.com
Ipe Notes
www.learnpick.in
3c3 Trigonomet Integrals Stu
www.slideshare.net
Https Ocw Mit Edu Resources Res 18 008 Calculus Revisited Complex Variables Differential Equations And Linear Algebra Fall 2011 Study Materials Mitres 18 008 Partiii Sol08 Pdf
2
2
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gctsci8qbernatxl6aenfh7n7hrgxvzgtwwvslxe7epgns6alrqw Usqp Cau
encrypted-tbn0.gstatic.com
Student Note Integration Techniques Fraction Mathematics Sine
es.scribd.com
Solved Interesting Fact Euler S Formula May Be Used To F Chegg Com
www.chegg.com
Elementary Calculus Reduction Formulas Sine And Cosine
www.vias.org
Lec 5 Integration Lecture Notes 5 Ufmfj9 30 1 Uwe Studocu
www.studocu.com
Mathematics Notes
www.learnpick.in
F X A 0 N 1 A 0 A 1 Cos X A 2 Cos 2x A 3 Cos 3x B 1 Sin X B 2 Sin 2x B 3 Sin 3x
docplayer.net
Trigonometric Integrals Special Methods Of Integration The Calculus Primer
schoolbag.info
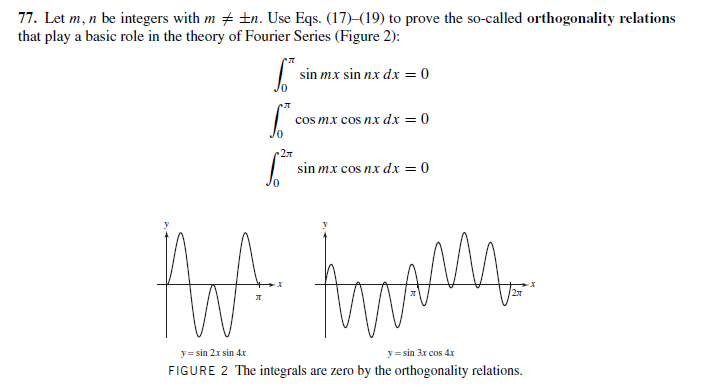
Calculus 2 How Do You Integrate 84 Of 300 Find The Integral Of Cos Mx Cos Nx Dx Youtube
www.youtube.com
Https Ocw Mit Edu Resources Res 18 008 Calculus Revisited Complex Variables Differential Equations And Linear Algebra Fall 2011 Study Materials Mitres 18 008 Partiii Sol08 Pdf
Definite Integration
www.slideshare.net
If I M N Int Sinx M Cosx N Dx Then Prove That I M N
doubtnut.com
Integral Of Cos Mx Cos Nx Youtube
www.youtube.com
Integral Docx
www.scribd.com
Introduction To Integral Calculus E D U C A T I O N
www.ibusciencecollege.com
3
encrypted-tbn0.gstatic.com
Pdf Trigonometric Integrals Jerome Delen Academia Edu
www.academia.edu
What Is The Integration Of Sin X Sin Nx Quora
www.quora.com
Powers Of Trig Functions
www.ltcconline.net
2
Https Sites Math Washington Edu Ep2 Classes 125 After Lesson14 Pdf
Integration Of A Product Of Sin M X Cos N X Youtube
www.youtube.com
Solved 2 Ftan Xdx A Consider N 1 Solve F Tan X Dx In Chegg Com
www.chegg.com
Https Ocw Mit Edu Resources Res 18 008 Calculus Revisited Complex Variables Differential Equations And Linear Algebra Fall 2011 Study Materials Mitres 18 008 Partiii Sol08 Pdf
7 2
studyres.com
