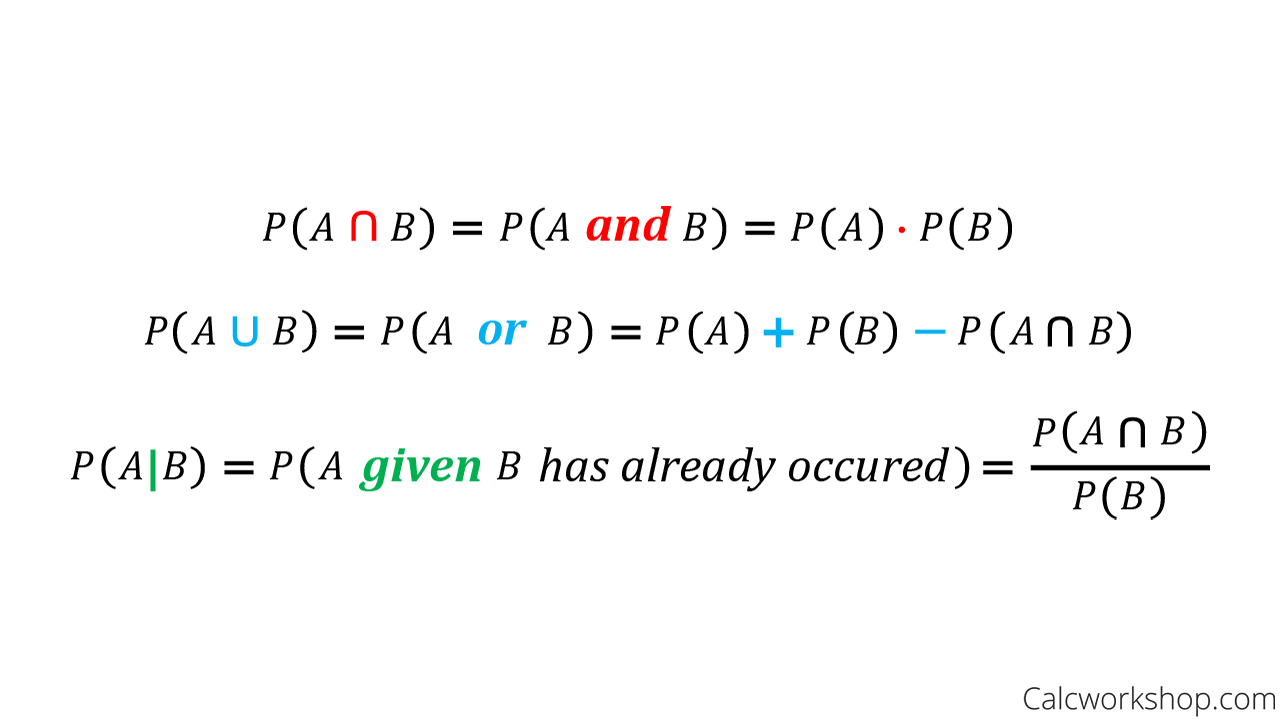Example Pab Formula
Given ex.

Example pab formula. For our first example suppose that we know the following values for probabilities. This is the product rule. If we got a red marble first the chance is now 24.
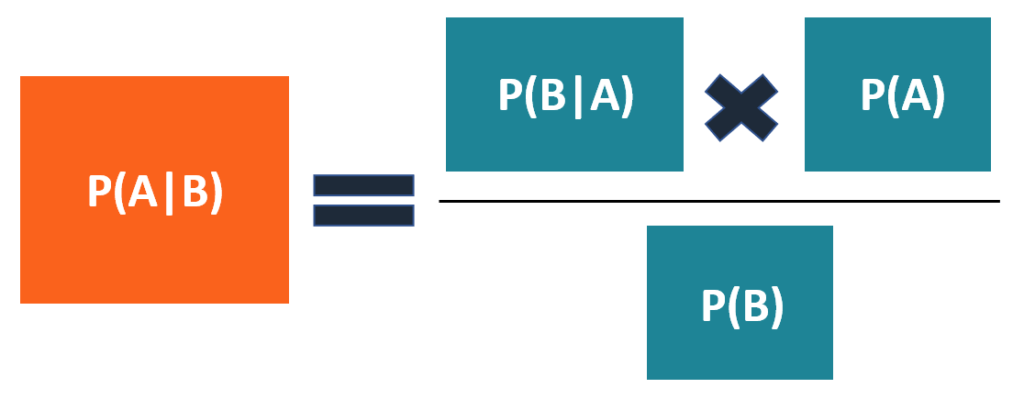
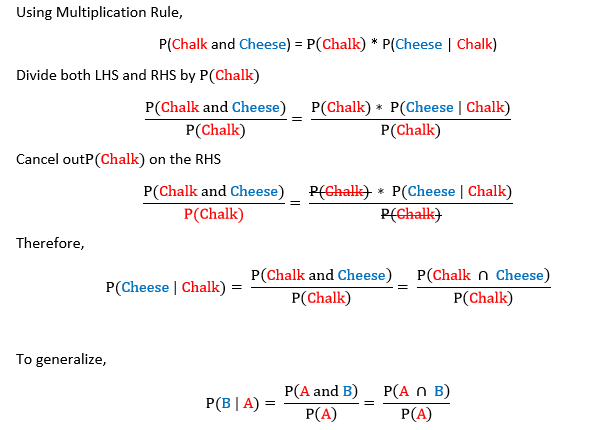
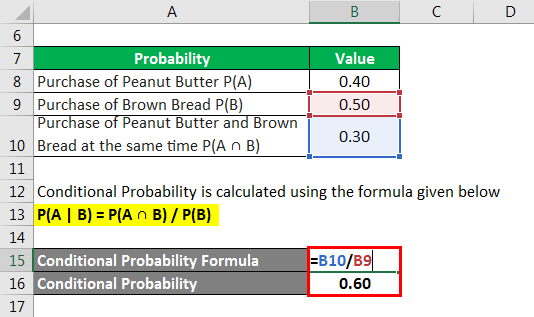
If we got a blue marble first the chance is now 14. Let us write the formula for conditional probability in the following format hspace100pt pa cap bpapbapbpab hspace100pt 15 this format is particularly useful in situations when we know the conditional probability but we are interested in the probability of the intersection. Cotter robability conditional probability discrete random variables definitions and formulas def.
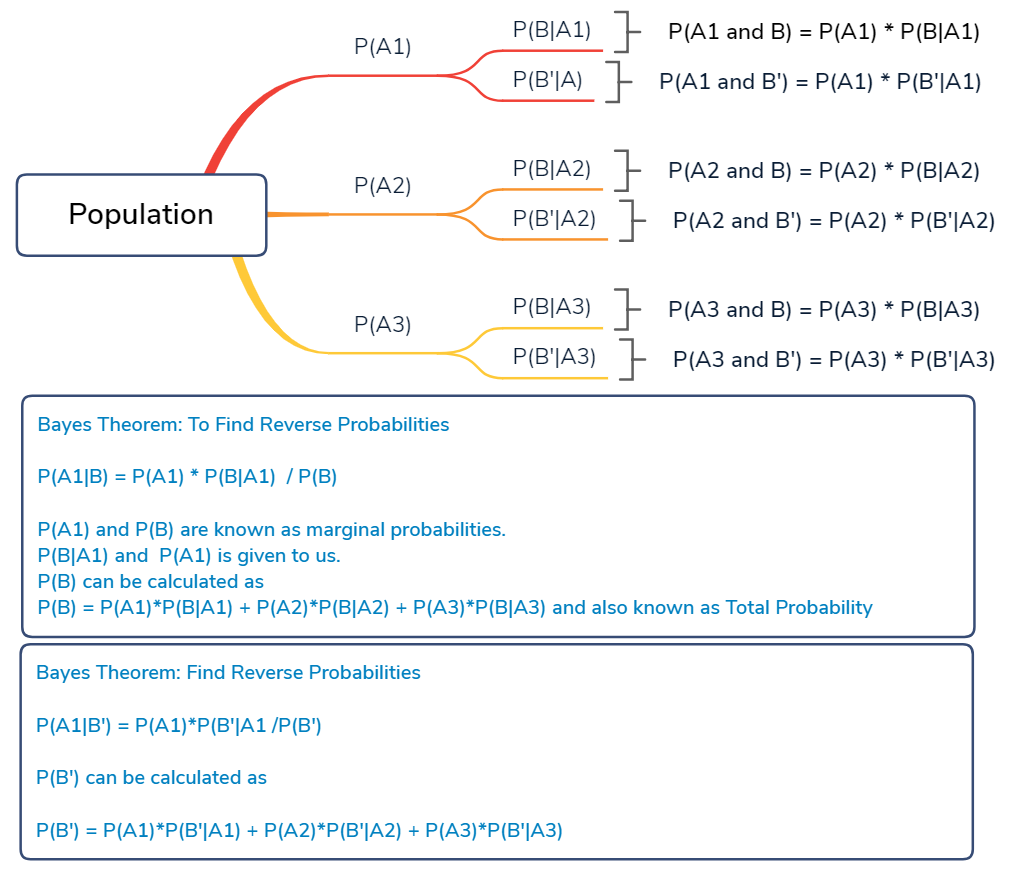
Another important method for calculating conditional probabilities is given by bayess formulathe formula is based on the expression pb pbapa pba cpa c which simply states that the probability of event b is the sum of the conditional probabilities of event b given that event a has or has not occurred. While the above example shows how the formula works it may not be the most illuminating as to how useful the above formula is. For independent events a and b this is equal to pbpa pbpa c p.
We can interpret this formula using a tree. To compensate for that double addition the intersection needs to be subtracted. And event b is get a blue marble second.
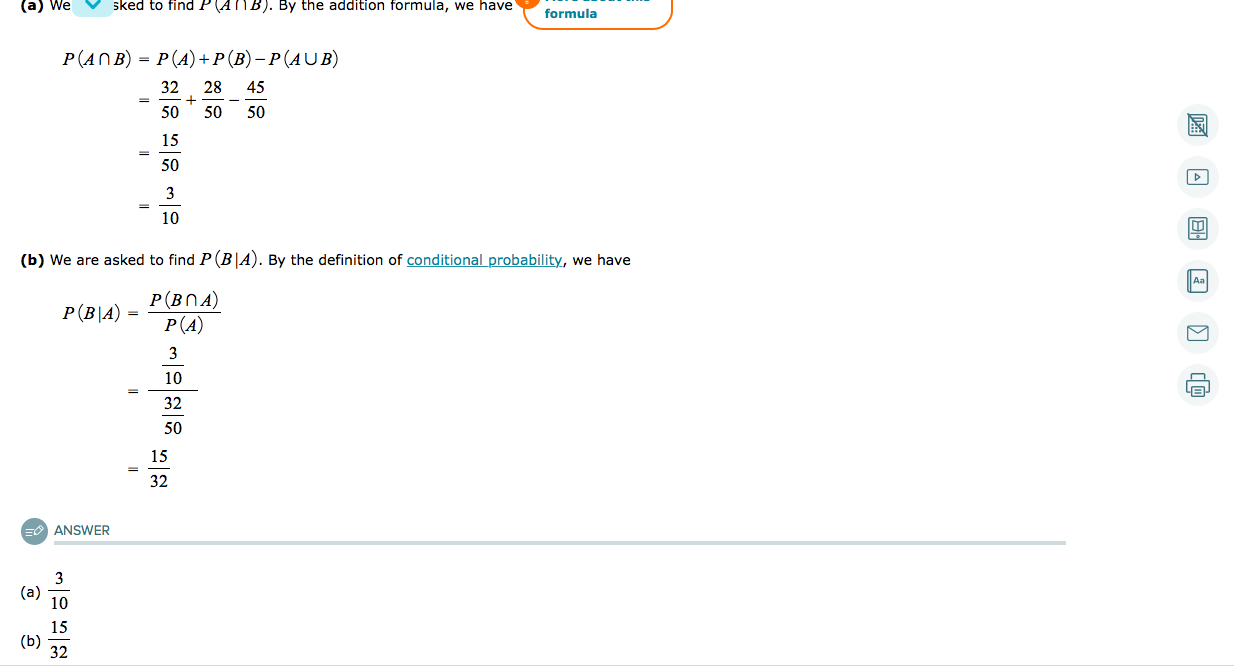
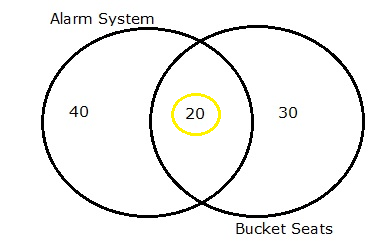
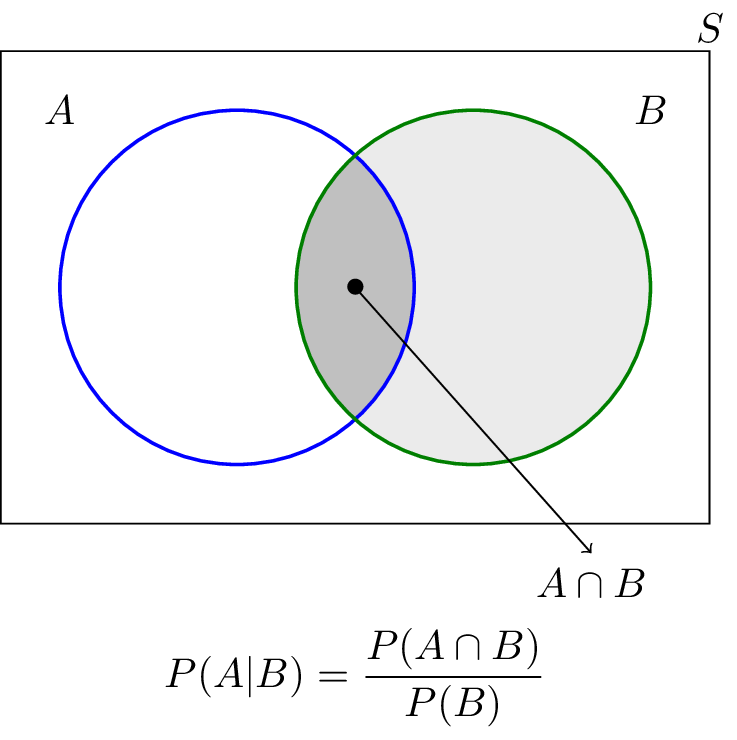
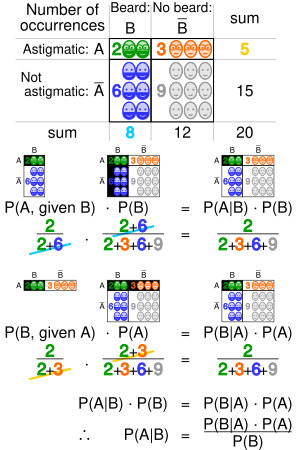
Independence two events a and b are called independent if pabpa ie if conditioning on one does not effect the probability of the other. Given two events a and b from the sigma field of a probability space with the unconditional probability of b being greater than zero ie pb0 the conditional probability of a given b is defined to be the quotient of the probability of the joint of events a and b and the probability of b. The probability pa b 08 x 05 04.
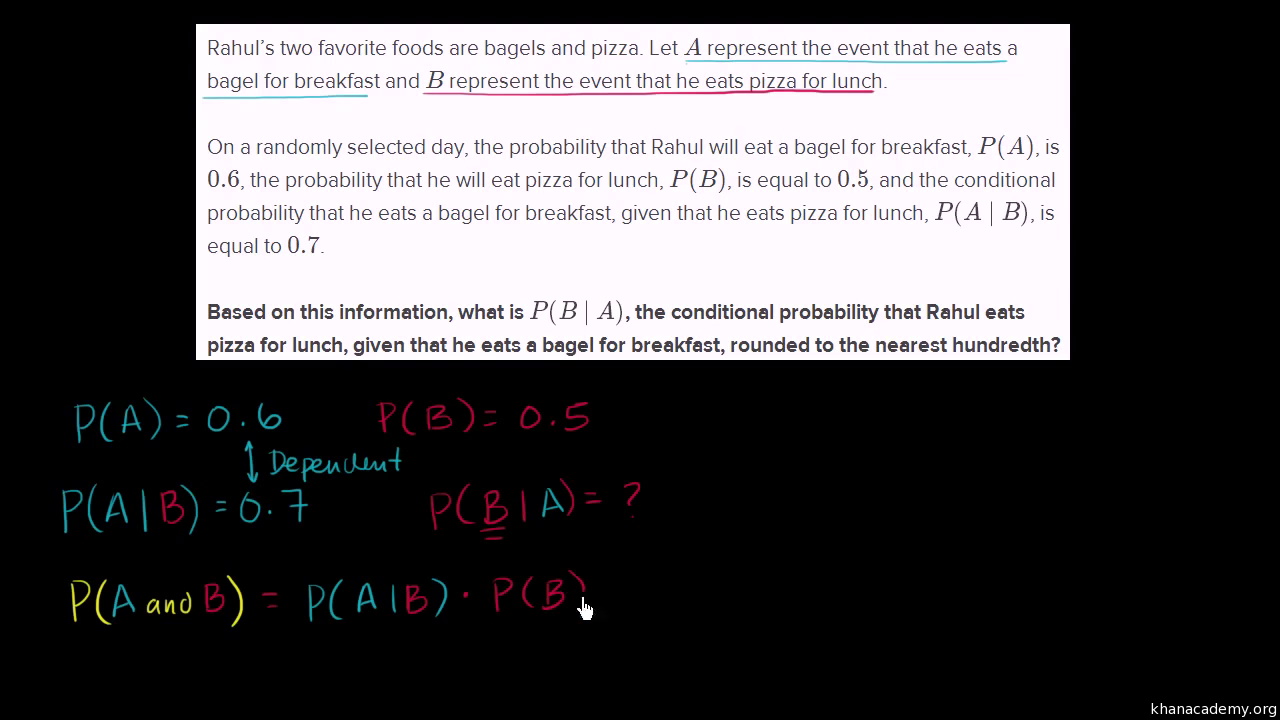
Pa means probability of event a in our marbles example event a is get a blue marble first with a probability of 25. If pa5 andpba4 pba4 5 2. Pab the conditional probability of a given b occurs notn.
For example if a it will snow today and if b it is 900 outside then knowing that. But for that we have 2 choices. The probability that event a occurs may change if we know event b has occurred.
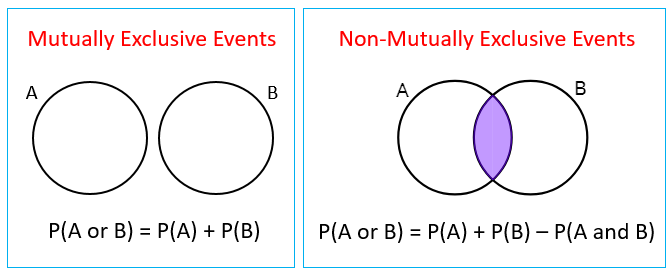
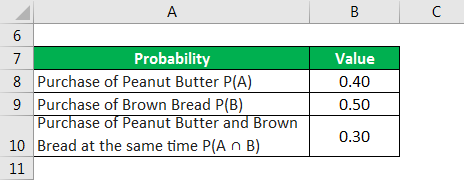
Pa or b pa pb pa and b example 2. When pa and pb are added the probability of the intersection and is added twice. Given pa 020 pb 070 pa and b 015.
.
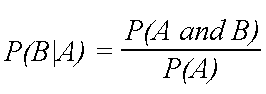

















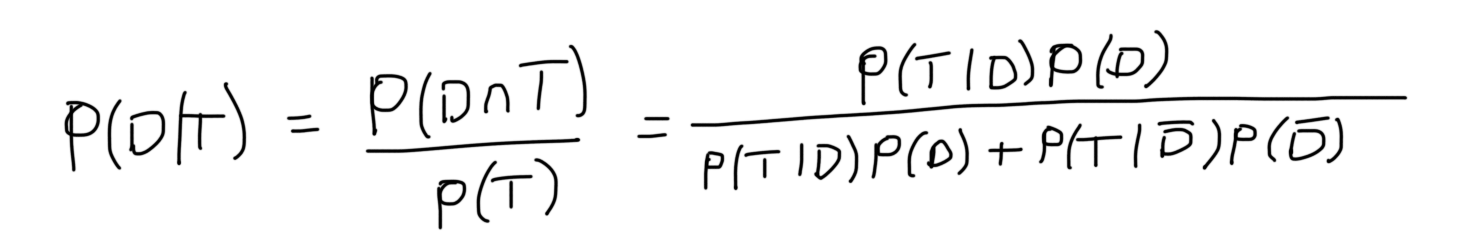









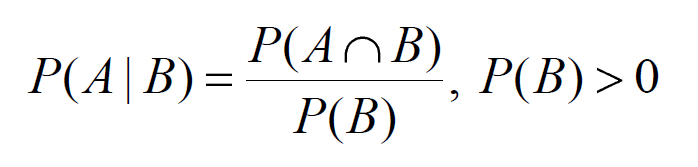



:max_bytes(150000):strip_icc()/conditional-56edf9de5f9b5867a1c1924c.jpg)



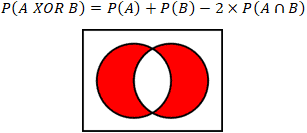



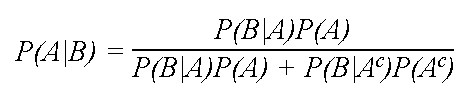




/conditional-56edf9de5f9b5867a1c1924c.jpg)
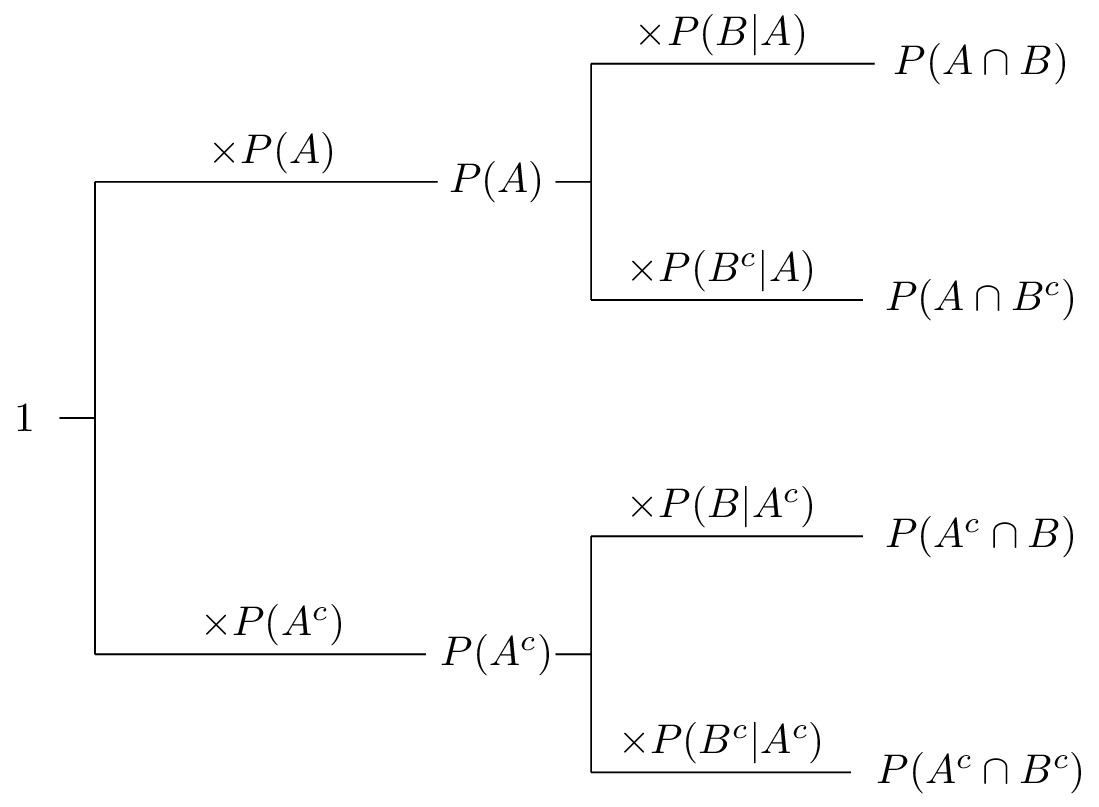



/conditional-56edf9de5f9b5867a1c1924c.jpg)


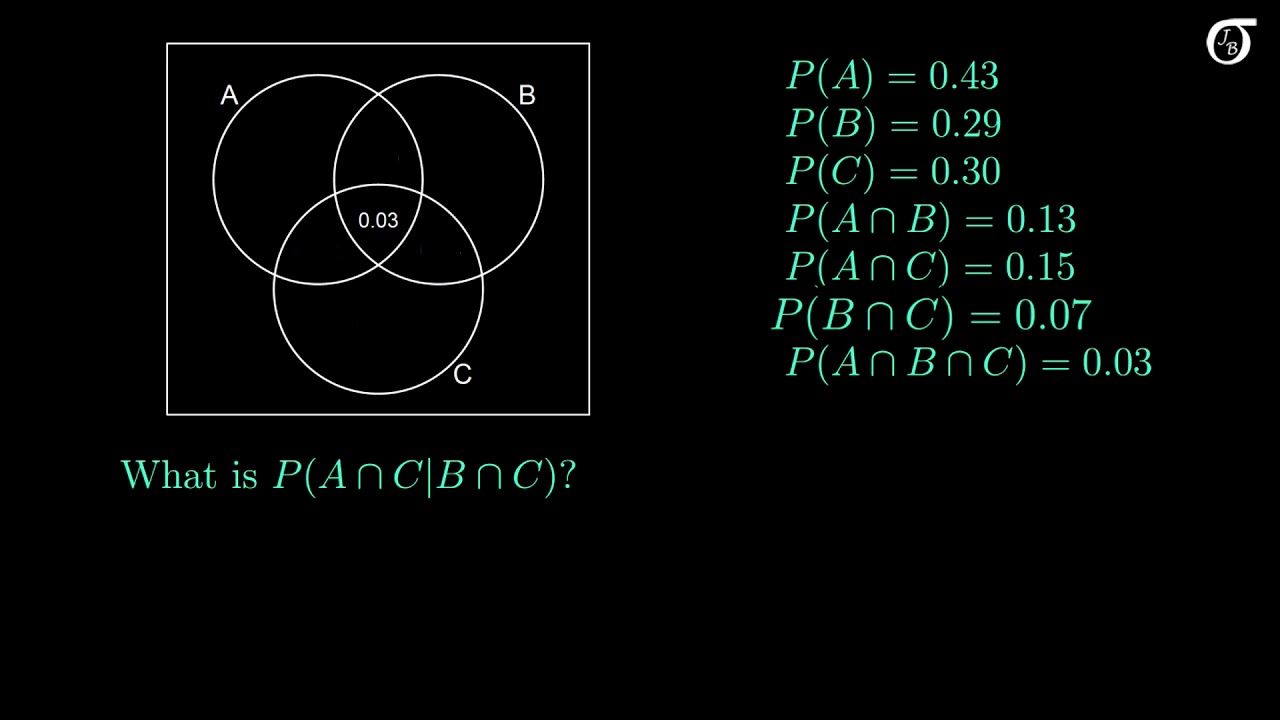







/JointProbabilityDefinition2-fb8b207be3164845b0d8706fe9c73b01.png)