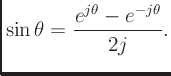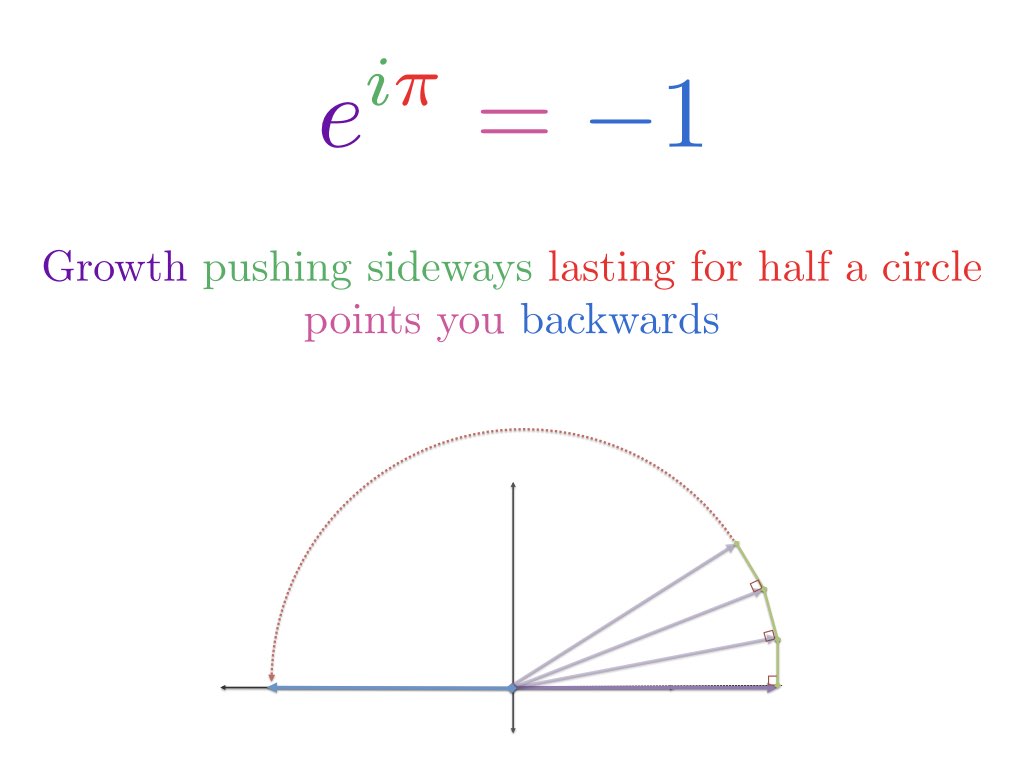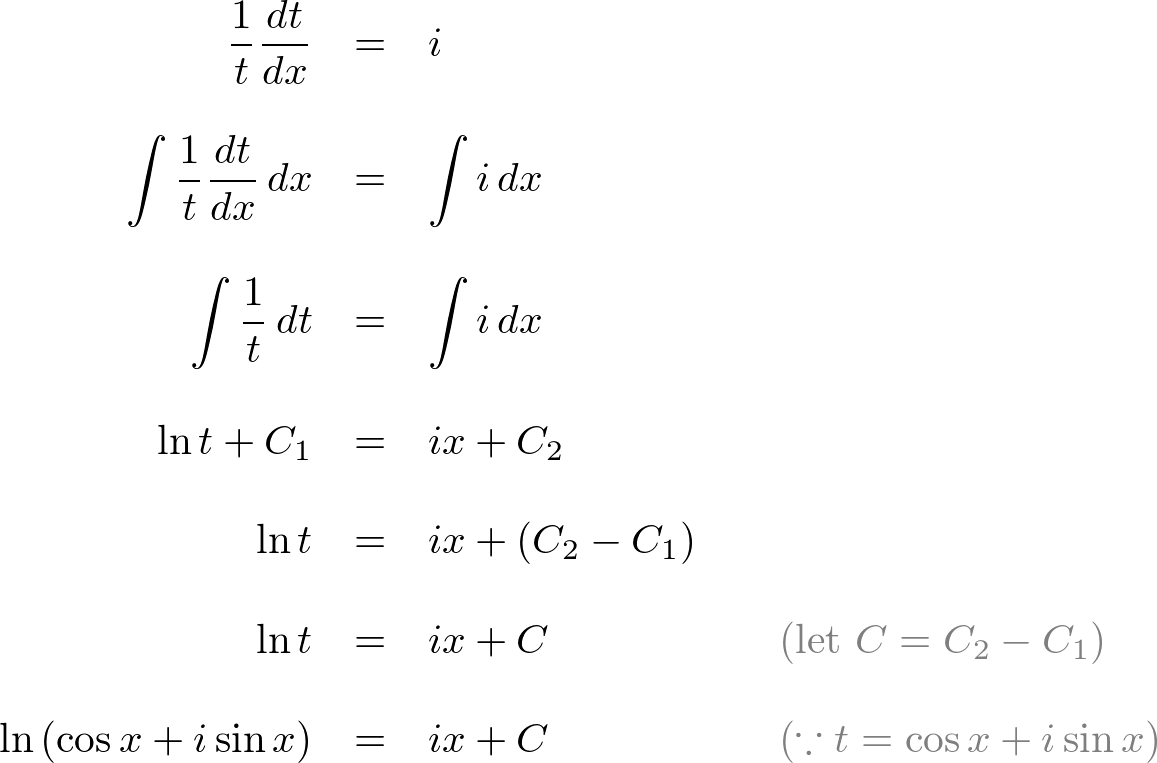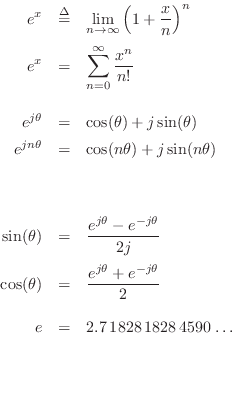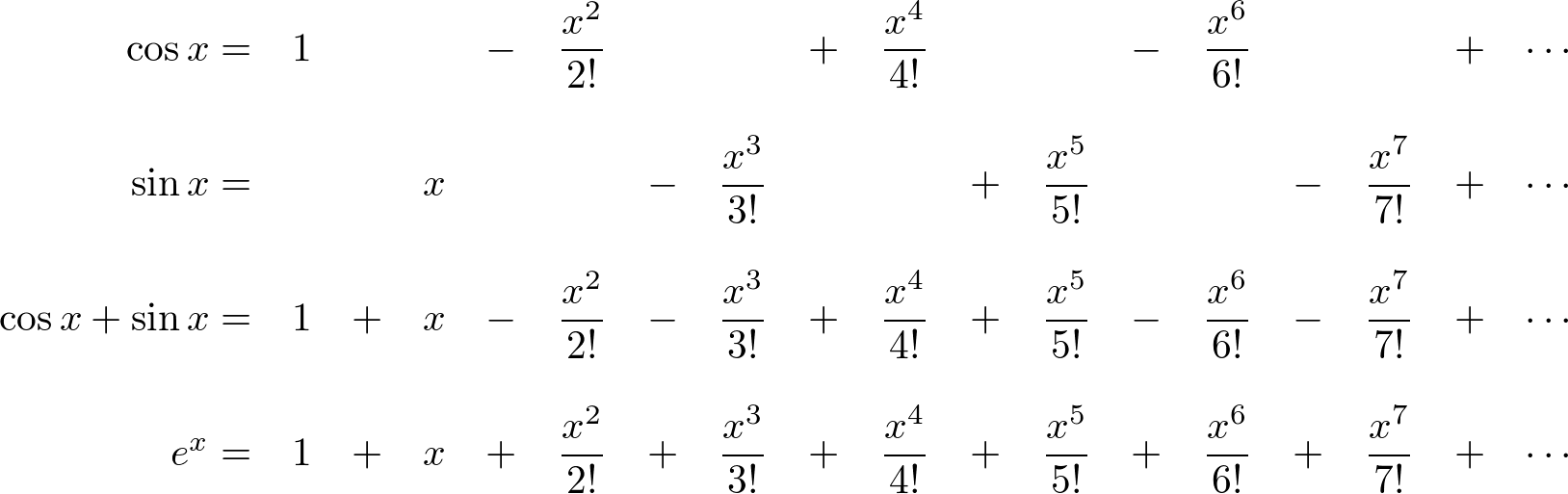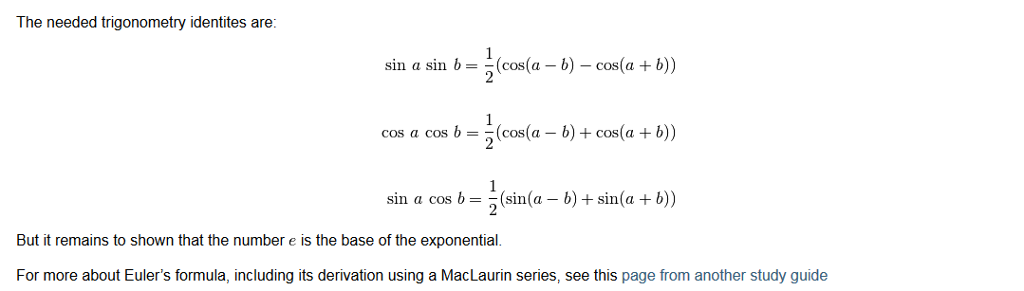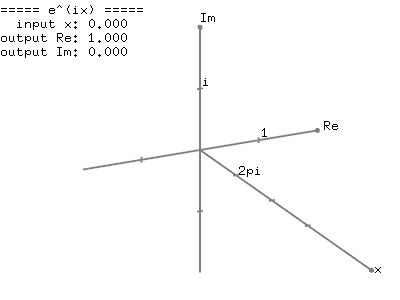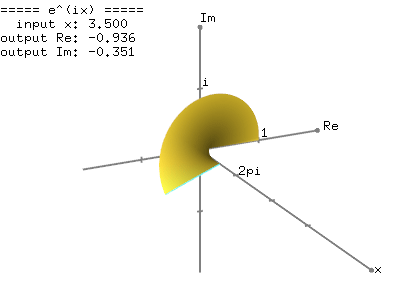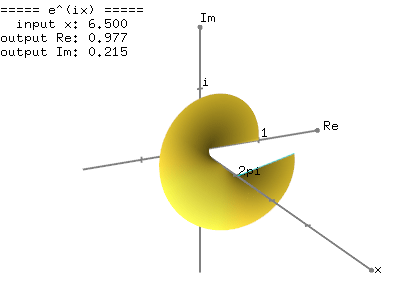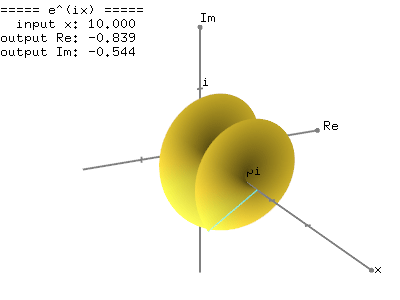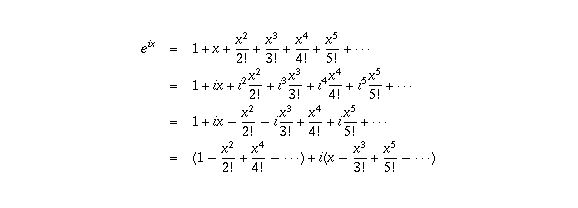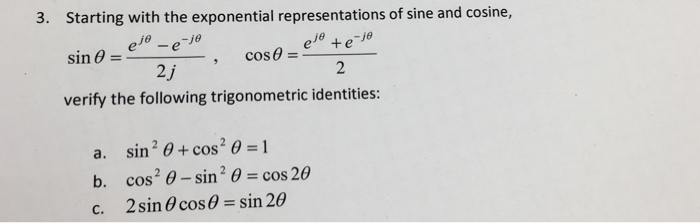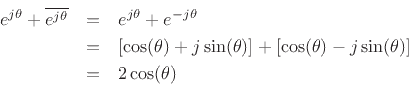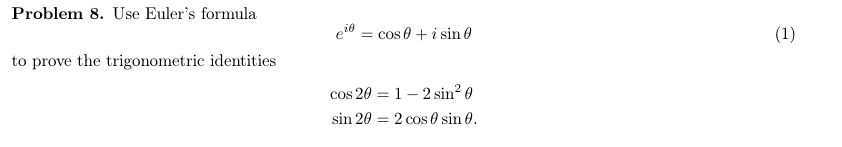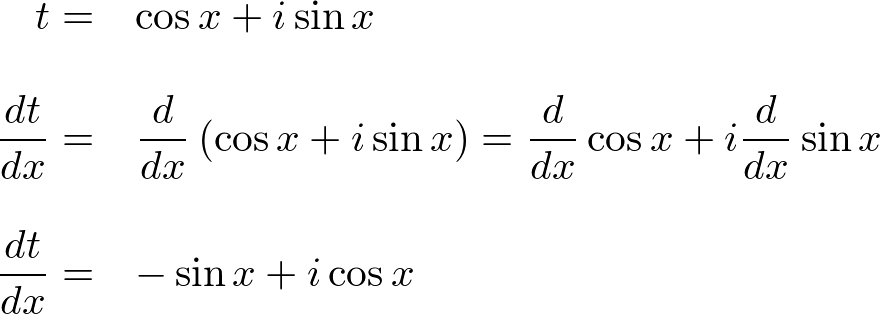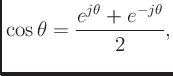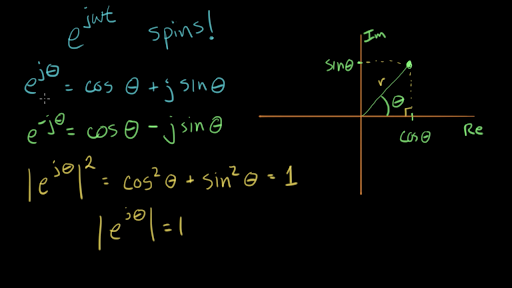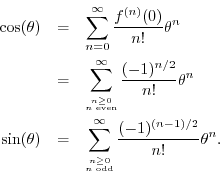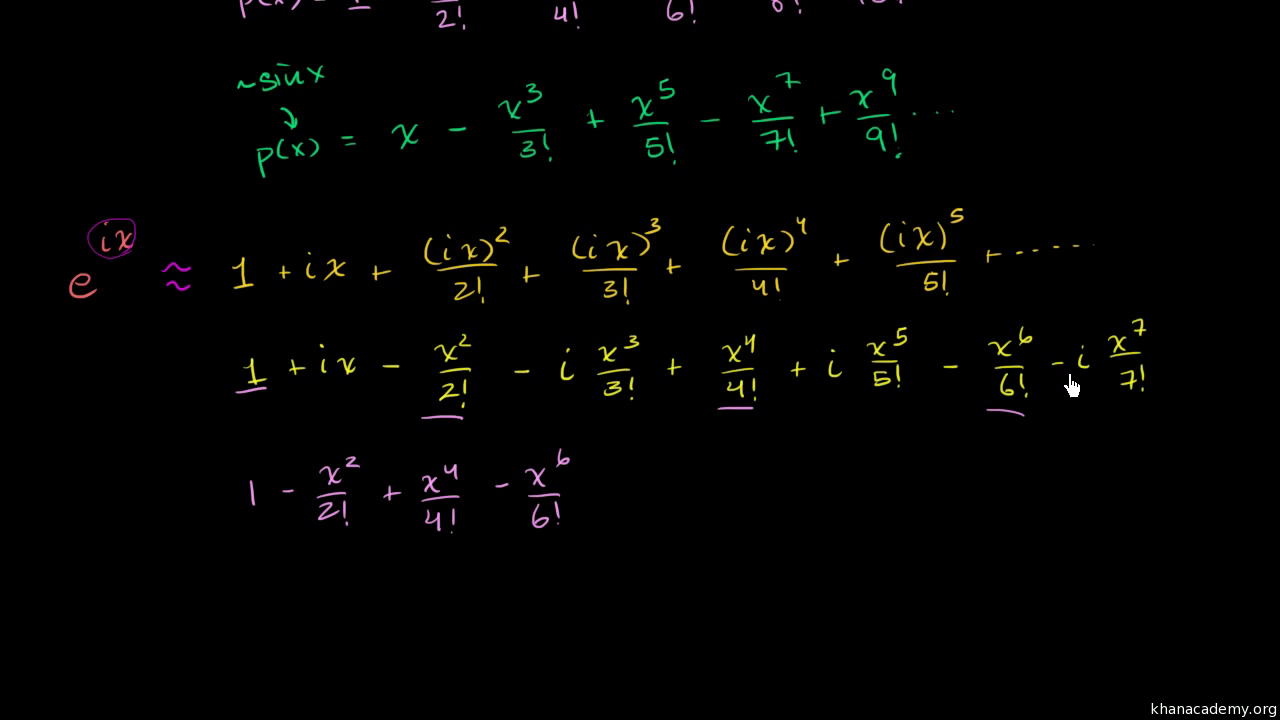E J Theta Formula
Basic Trigonometric Functions Trigonometry Socratic
socratic.org
Pdf Explicit Arithmetic Intersection Theory And Computation Of N Eron Tate Heights
www.researchgate.net
The Final Problem An Account Of The Mock Theta Functions Watson 1936 Journal Of The London Mathematical Society Wiley Online Library
londmathsoc.onlinelibrary.wiley.com
Euler S Formula And Trig Identities Steve On Image Processing And Matlab Matlab Simulink
blogs.mathworks.com
Euler S Formula Math Images
mathimages.swarthmore.edu
Euler S Formula For Complex Numbers
www.mathsisfun.com
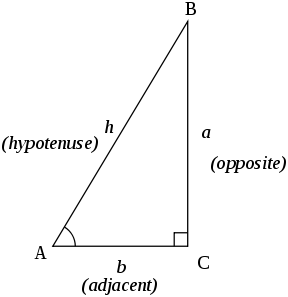
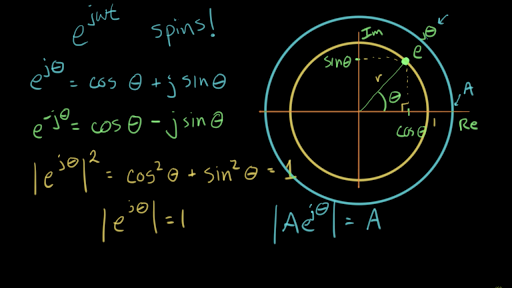
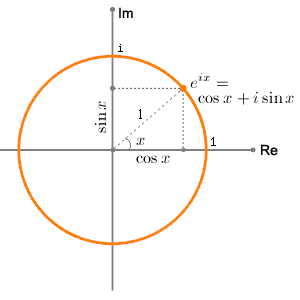
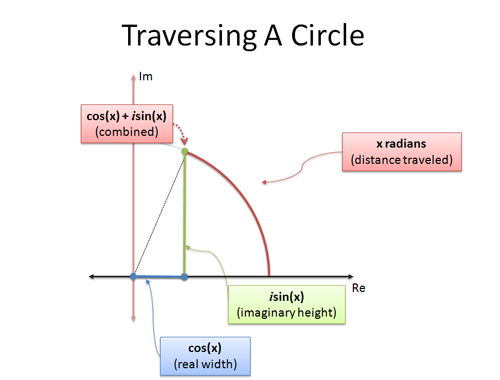
Ej cos jsin 1 where j 1.
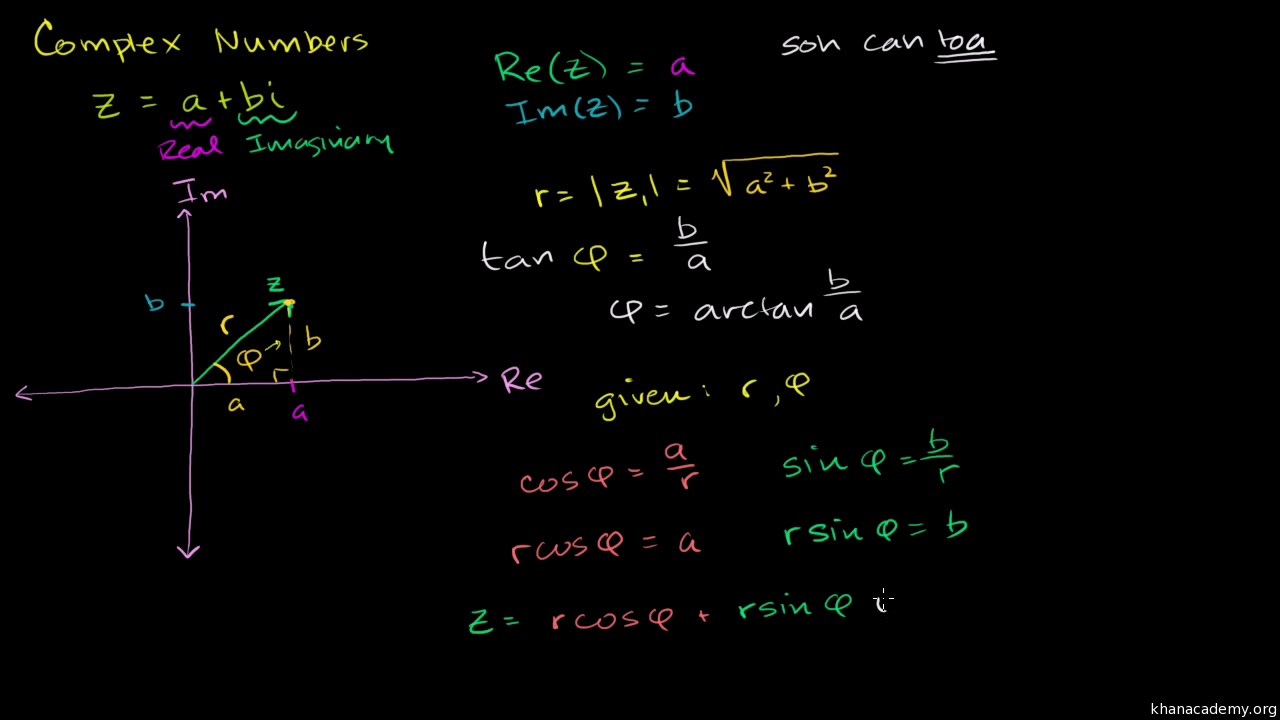
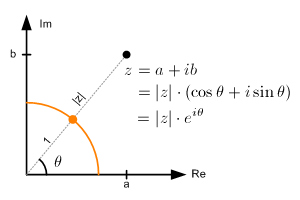
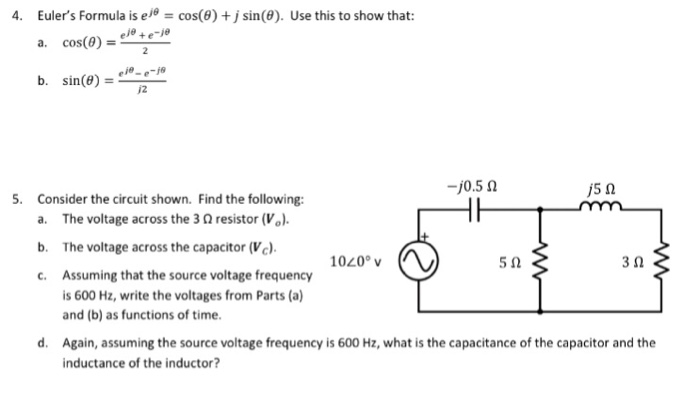
E j theta formula. We simply give a magnitude a and an angle theta that a complex number makes with the real axis the arc tangent of the imaginary over the real component and we can express it using eulers formula. 4 if you are curious you can verify these fairly quickly by plugging 1 into the. Using eulers formula e jtheta costheta j sintheta express ejpi4 as a complex number a jb and find the numerical values of a and b.
The arguments of trigonometric functions are in radians and not in degrees. And seeing that this is identical to the power series for cos isin. E cos j sin evaluate ejpib raised to the power 4 using eulers formula and express the result as a complex.
Justifications that e i cos i sin e i x cos x i sin x justification 1. Eulers formula then comes about by extending the power series for the expo nential function to the case of x i to get expi 1 i 2 2. 4 applications of eulers formula 41 trigonometric identities.
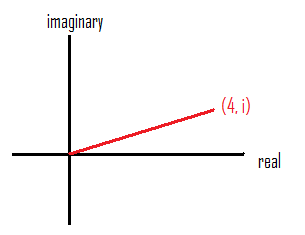
Since is its own derivative the taylor series expansion for. Is one of the simplest imaginable infinite series. For instance we can express the number 1 i as.
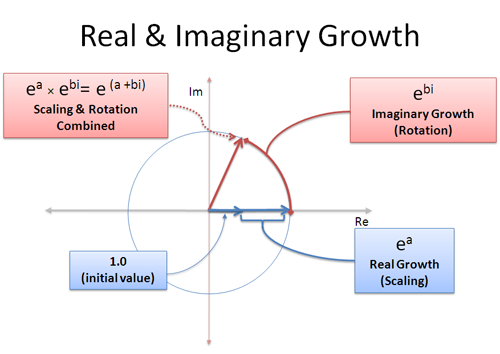
Ej theta weve now defined for any positive real number and any complex number. Eulers formula for complex exponentials according to euler we should regard the complex exponential eit as related to the trigonometric functions cost and sint via the following inspired denitioneit cos ti sin t where as usual in complex numbers i2 1. 2 note that a consequence of the euler identity is that cos ej e j 2 3 and sin jej je j 2.
1 the justication of this notation is based on the formal derivative of both sides. Where e is the base of the natural logarithm i is the imaginary unit and cos and sin are the trigonometric functions. Eulers formula named after leonhard euler is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential functioneulers formula states that for any real number x.
3 2 Complex Numbers Theoretical Physics Reference 0 5 Documentation
www.theoretical-physics.net
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcsuxynf3wxj3tgzemlkx9chuv4r5grlqneuqq Usqp Cau
Inverse Euler Formulas
musicweb.ucsd.edu
hi.wikipedia.org
3 2 Complex Numbers Theoretical Physics Reference 0 5 Documentation
www.theoretical-physics.net
Intuitive Understanding Of Euler S Formula Betterexplained
betterexplained.com
Trigonometric Functions Wikiwand
www.wikiwand.com
Solved Using Euler S Formula E Jtheta Cos Theta J Sin Chegg Com
www.chegg.com
The Amplitude Of E E Itheta Where Theta In R And I Sqrt 1 Is Youtube
www.youtube.com
Machine Learning By Stanford Backpropagation In Practice Gradient Checking
pvgisours.tistory.com
Intuitive Understanding Of Euler S Formula Betterexplained
betterexplained.com
Why Is Math E I Theta Cos Theta I Sin Theta Math Quora
www.quora.com
Euler S Formula Wikipedia
en.wikipedia.org
Christopher J Tralie Ph D
www.ctralie.com
Solved Some Useful Formulas Cos Theta E J Theta E J Chegg Com
www.chegg.com
Why Is Math E I Theta Cos Theta I Sin Theta Math Quora
www.quora.com
Euler S Equation
www.songho.ca
Euler S Formula Wikipedia
en.wikipedia.org
Solved Employ Euler S Formula To Show That A Cos Theta Chegg Com
www.chegg.com
Complex Definitions Of Sine And Cosine Youtube
www.youtube.com
Pdf Ramanujan S Theta Function Identities Involving Lambert Series
www.researchgate.net
Proof Of Euler S Equation Exp Ix Cos X Isin X Youtube
www.youtube.com
Proof Of Euler S Identity Mathematics Of The Dft
www.dsprelated.com
Using Euler S Relation Derive The Following Relat Chegg Com
www.chegg.com
Complex And Trigonometric Identities Introduction To Digital Filters
www.dsprelated.com
Euler S Equation
www.songho.ca
Intuitive Understanding Of Euler S Formula Betterexplained
betterexplained.com
Solved Write A C Program That Demonstrates The Correctnes Chegg Com
www.chegg.com
Why Is Math E I Theta Cos Theta I Sin Theta Math Quora
www.quora.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gctococbz Zfdhqltkcrch 7pcjl6imkf87rrw Usqp Cau
Euler S Formula For Complex Numbers
www.mathsisfun.com
Euler S Formula Wikipedia
en.wikipedia.org
Complex Exponential Magnitude Video Khan Academy
www.khanacademy.org
2
Question Corner Why Is E Pi I 1
www.math.toronto.edu
Complex Exponentials Spin Video Khan Academy
www.khanacademy.org
Pdf Two New Relations Between Q Product Identities Theta Function Identities And Combinatorial Partition Identities
www.researchgate.net
2
Why Is Math E I Theta Cos Theta I Sin Theta Math Quora
www.quora.com
Intro To Quantum 5 B Convert Cos And Sin To Complex Exponential Youtube
www.youtube.com
Why Is Math E I Theta Cos Theta I Sin Theta Math Quora
www.quora.com
Euler S Formula And Trig Identities Steve On Image Processing And Matlab Matlab Simulink
blogs.mathworks.com
15 2 Complex Numbers In Polar And Exponential Form
mathonweb.com
Solved Using Euler S Formula E I Theta Cos Theta I S Chegg Com
www.chegg.com
Resolucao Equacao Grau 6 En Resolution Of Sixth Degree Algebraic Equations By Docsity
www.docsity.com
Euler S Equation
www.songho.ca
Euler S Equation
www.songho.ca
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcrejftp2zql5ll8uzog20ypzi 5zp3x Cxg3drkriy Usqp Cau
encrypted-tbn0.gstatic.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gctsgq Elmvsmf2tddml37vc8sw42sc2ir0h Xxujjv85fhi6tkb Usqp Cau
encrypted-tbn0.gstatic.com
Why Is Math E I Theta Cos Theta I Sin Theta Math Quora
www.quora.com
Euler S Formula Wikipedia
en.wikipedia.org
1
encrypted-tbn0.gstatic.com
Solved Assuming That The Numbers Theta A B Alpha Omega Chegg Com
www.chegg.com
Euler S Formula Wikipedia
en.wikipedia.org
Pdf Some New Modular Equations Of Degree Four And Their Explicit Evaluations
www.researchgate.net
Euler S Formula Wikipedia
en.wikipedia.org
Euler S Formula Wikipedia
en.wikipedia.org
Theta Function Wikipedia
en.wikipedia.org
Euler S Formula Wikipedia
en.wikipedia.org
Solved Starting With The Exponential Representations Of S Chegg Com
www.chegg.com
Why Is Math E I Theta Cos Theta I Sin Theta Math Quora
www.quora.com
List Of Trigonometric Identities Wikipedia
en.wikipedia.org
Solved Using Euler S Formula E J Theta Cos Theta J S Chegg Com
www.chegg.com
Intuitive Understanding Of Euler S Formula Betterexplained
betterexplained.com
Theta Function Wikipedia
en.wikipedia.org
Phasor Wikipedia
en.wikipedia.org
If Z R E Itheta Then Prove That E I Z E R S Inthetadot Youtube
www.youtube.com
Solved Using Euler S Formula E Plus Minusj Theta Cos The Chegg Com
www.chegg.com
Solved Using Euler S Formula E Plusminusjtheta Cos Thet Chegg Com
www.chegg.com
Https Www Jstor Org Stable 270831
Solved A Use Euler S Formula Eq 2 8 To Show That Cos Chegg Com
www.chegg.com
A Mind Dump Of Mathematics Complex Numbers
minddumpofmath.blogspot.com
Euler S Identity
ccrma.stanford.edu
Dr Dtheta R Sec Theta Cos Theta Linear Differential Equation Youtube
www.youtube.com
Solved Use Euler S Formula E I Theta Cos Theta I Sin Chegg Com
www.chegg.com
Euler S Equation
www.songho.ca
2
Engineering
www-engineering.blogspot.com
Christopher J Tralie Ph D
www.ctralie.com
Inverse Euler Formulas
musicweb.ucsd.edu
Sampling Theorem
ccrma.stanford.edu
3 2 Complex Numbers Theoretical Physics Reference 0 5 Documentation
www.theoretical-physics.net
Complex Exponential Magnitude Video Khan Academy
www.khanacademy.org
Euler S Formula For Complex Numbers
www.mathsisfun.com
Group Delay Of H Omega 1 Re J Theta E J Omega Signal Processing Stack Exchange
dsp.stackexchange.com
E Ix Deriving Euler S Formula Tanton Mathematics Youtube
www.youtube.com
Intuitive Understanding Of Euler S Formula Betterexplained
betterexplained.com
Proof Of Euler S Identity Mathematics Of The Dft
www.dsprelated.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqt73ivvpbnhpfppm1foxkhgl16ztkrrawseqjsf5gmxaxiykcs Usqp Cau
encrypted-tbn0.gstatic.com
How To Find Calculate The Activation Energy From This Constant In Arrhenius Equation
www.researchgate.net
Polar Form Of Complex Numbers Both With Cis With E Euler S Formula Youtube
www.youtube.com
15 2 Complex Numbers In Polar And Exponential Form
mathonweb.com
Absolute Value Angle Of Complex Numbers Video Khan Academy
www.khanacademy.org
Why Is Math E I Theta Cos Theta I Sin Theta Math Quora
www.quora.com
4 Polar Form Of Complex Numbers
www.intmath.com
Chp3 Matlab Functions Part1 Ppt Video Online Download
slideplayer.com
Solved Euler S Formula Is E J Theta Cos Theta J Sin Chegg Com
www.chegg.com
Euler S Formula Euler S Identity Video Khan Academy
www.khanacademy.org
