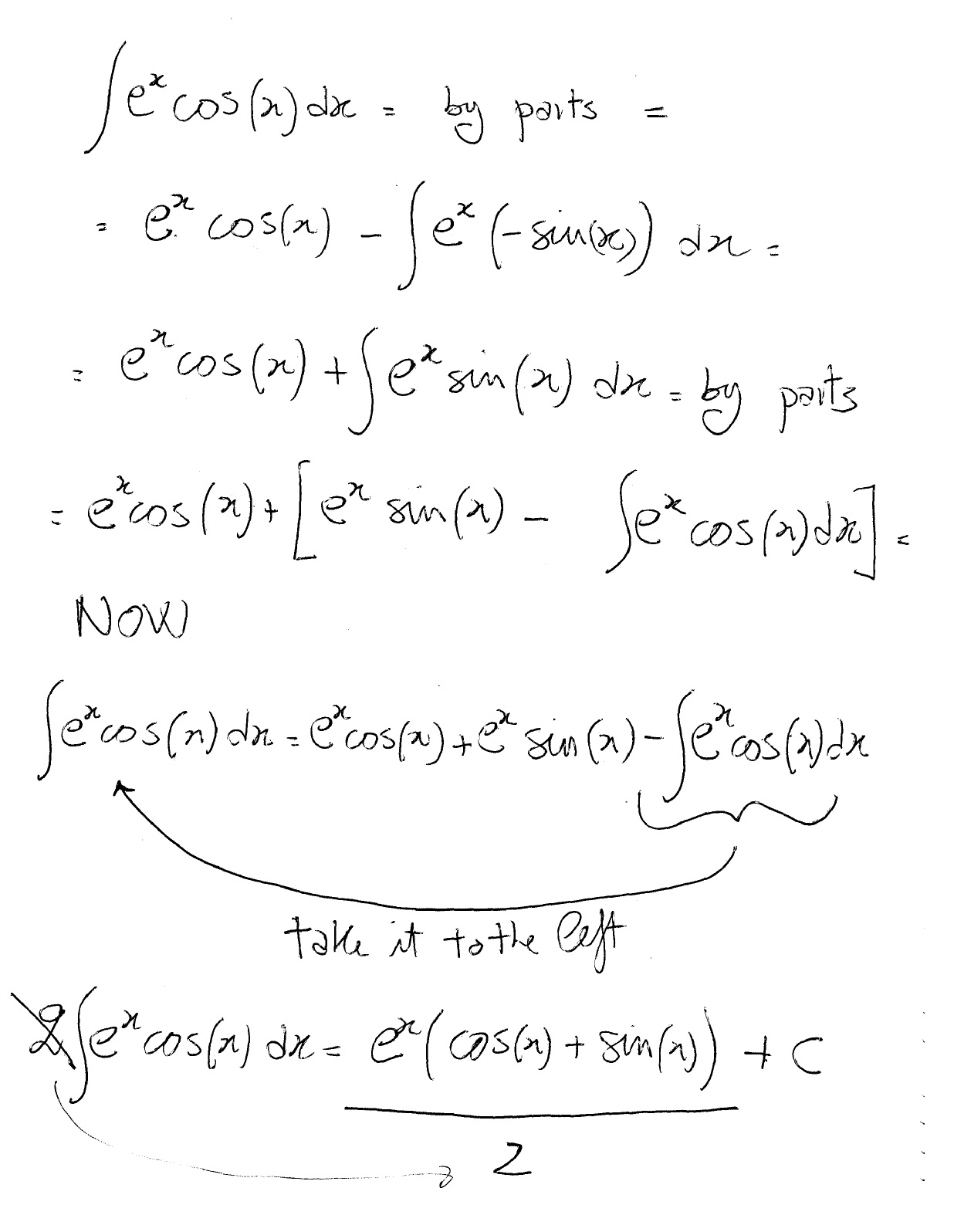Differentiate Ex Formula
And i will tell you and this is an amazing thing that that is indeed true that if i have some function f of x that is equal to e to the x and if i were to take the derivative of this this is going to be equal to e to the x as well or another way of saying it the derivative with respect to x of e to the x is equal to e to the x and that is.
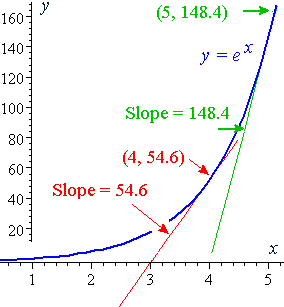
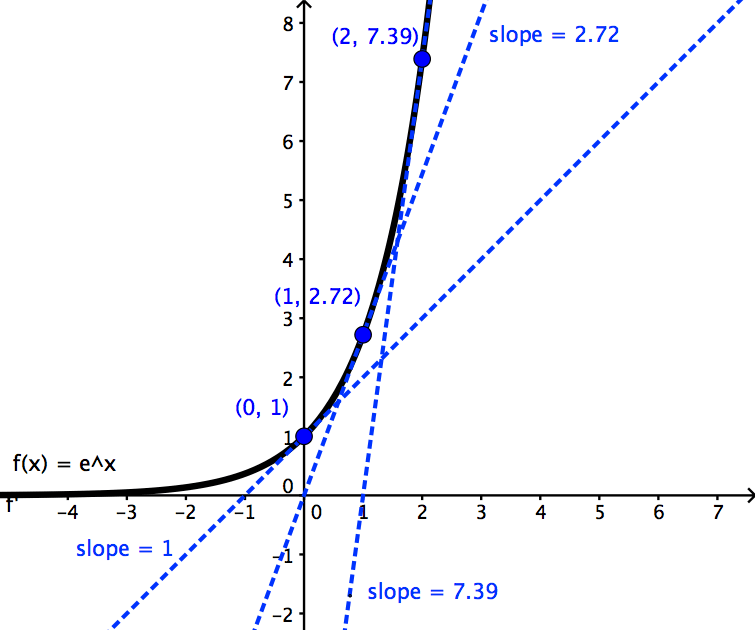
Differentiate ex formula. For real numbers c and d a function of the form is also an exponential function since it can be rewritten as. The derivative of e x is e x. Since the derivative of e x is e x then the slope of the tangent line at x 2 is also e 2 739.
Type in any function derivative to get the solution steps and graph. You can also check your answers. Differentiation of exponential and logarithmic functions exponential functions and their corresponding inverse functions called logarithmic functions have the following differentiation formulas.
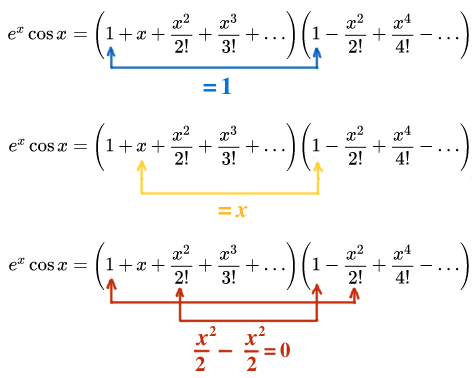
Others can be verified by using the definition of the derivative. This pattern suggests the following general formula for powers of n where n is a positive integer. This is one of the properties that makes the exponential function really important.
The derivative calculator supports computing first second fifth derivatives as well as differentiating functions with many variables partial derivatives implicit differentiation and calculating rootszeros. The prior section showed how to differentiate the general case of an exponential function with any constant as the base. Note that the exponential function f x e x has the special property that its derivative is the function itself f x e x f x.
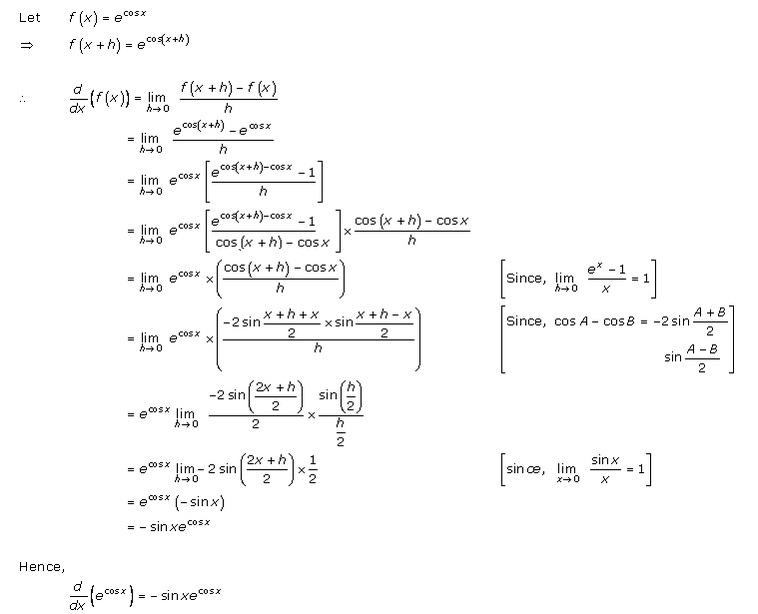
We can now apply that to calculate the derivative of other functions involving the exponential. Dexdxex what does this mean. This is one of the most important topics in higher class mathematics.
At this point the y value is e 2 739. Free derivative calculator differentiate functions with all the steps. This formula list includes derivative for constant trigonometric functions polynomials hyperbolic logarithmic.
A differentiation formulas list has been provided here for students so that they can refer to these to solve problems based on differential equations. Interactive graphsplots help visualize and better understand the functions. Extending the proof for the derivative of e x.
We only needed it here to prove the result above. It means the slope is the same as the function value the y value for all points on the graph. Choose the special example.
Now you can forget for a while the series expression for the exponential. In fact the power rule is valid for any real number n and thus can be used to differentiate a variety of non polynomial functions. Next select the special case where the base is the exponential constant.
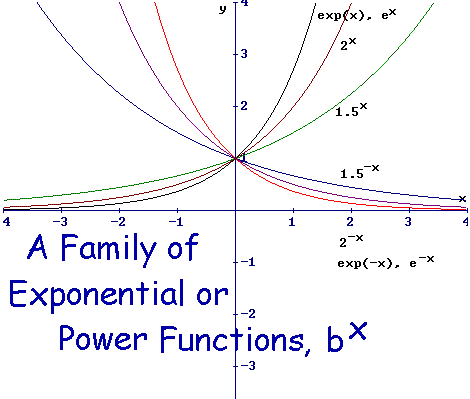
Where b is a positive real number not equal to 1 and the argument x occurs as an exponent.


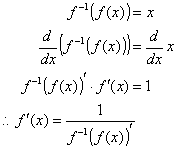


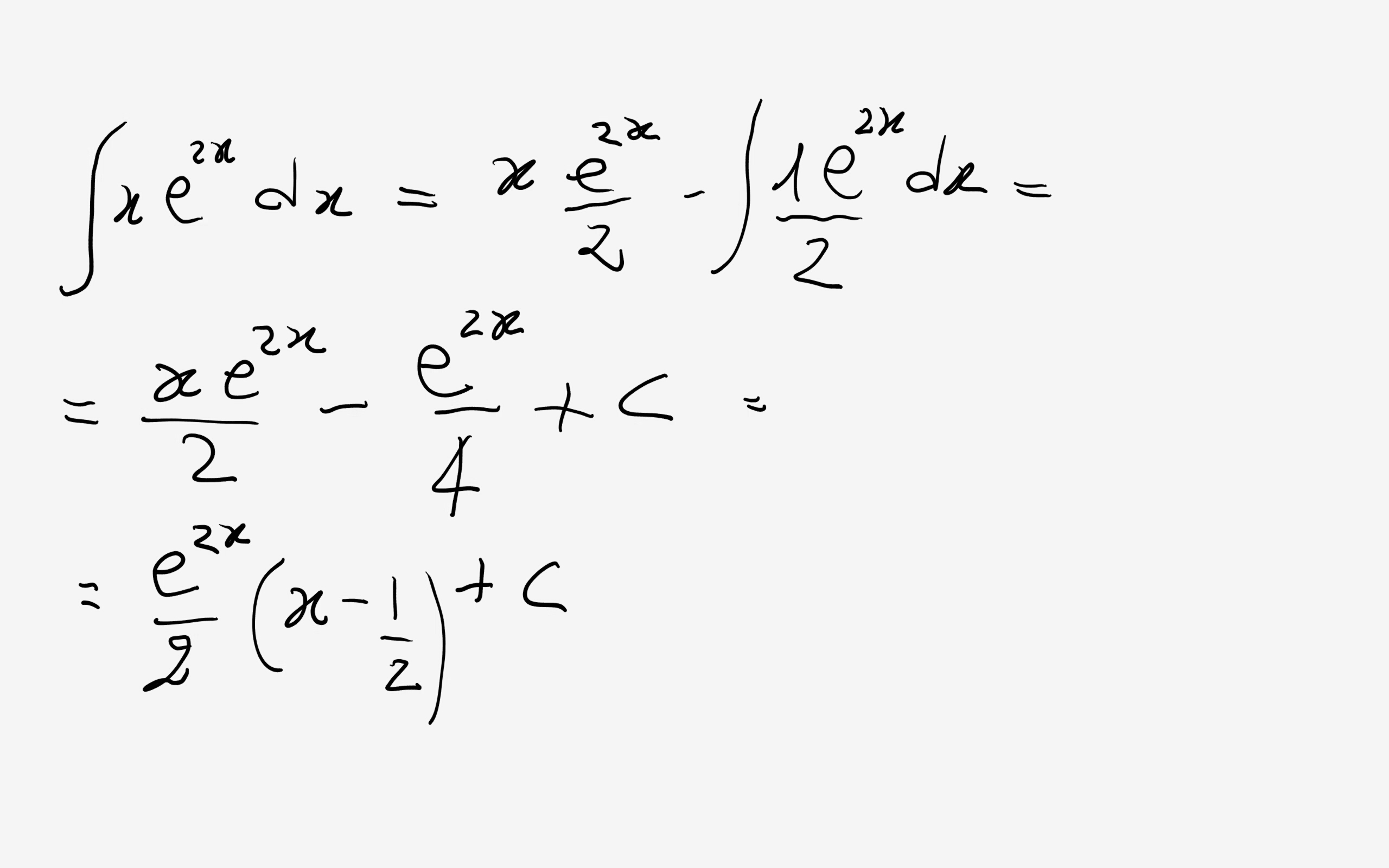





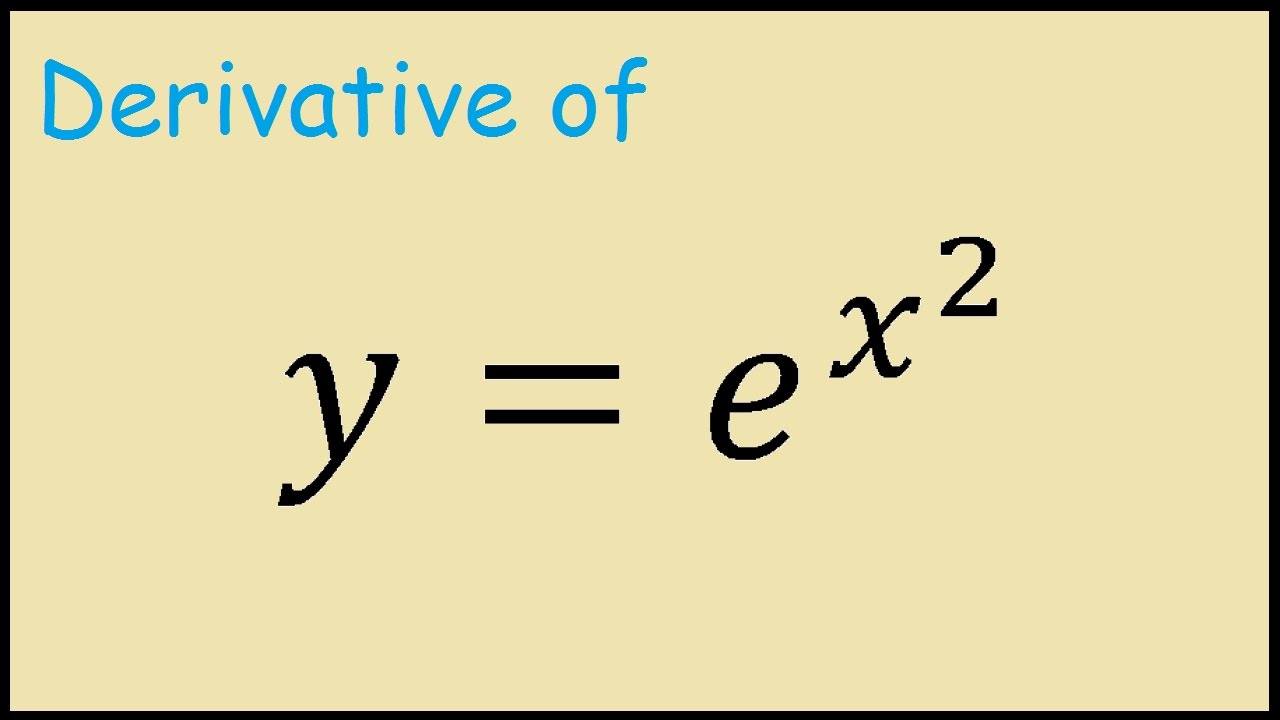




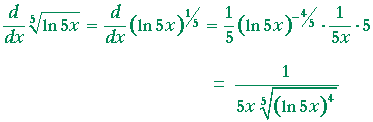






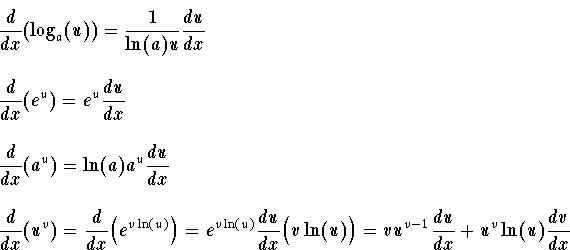

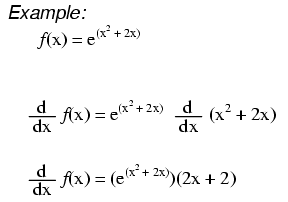





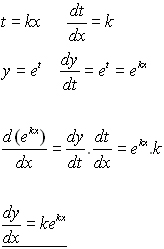





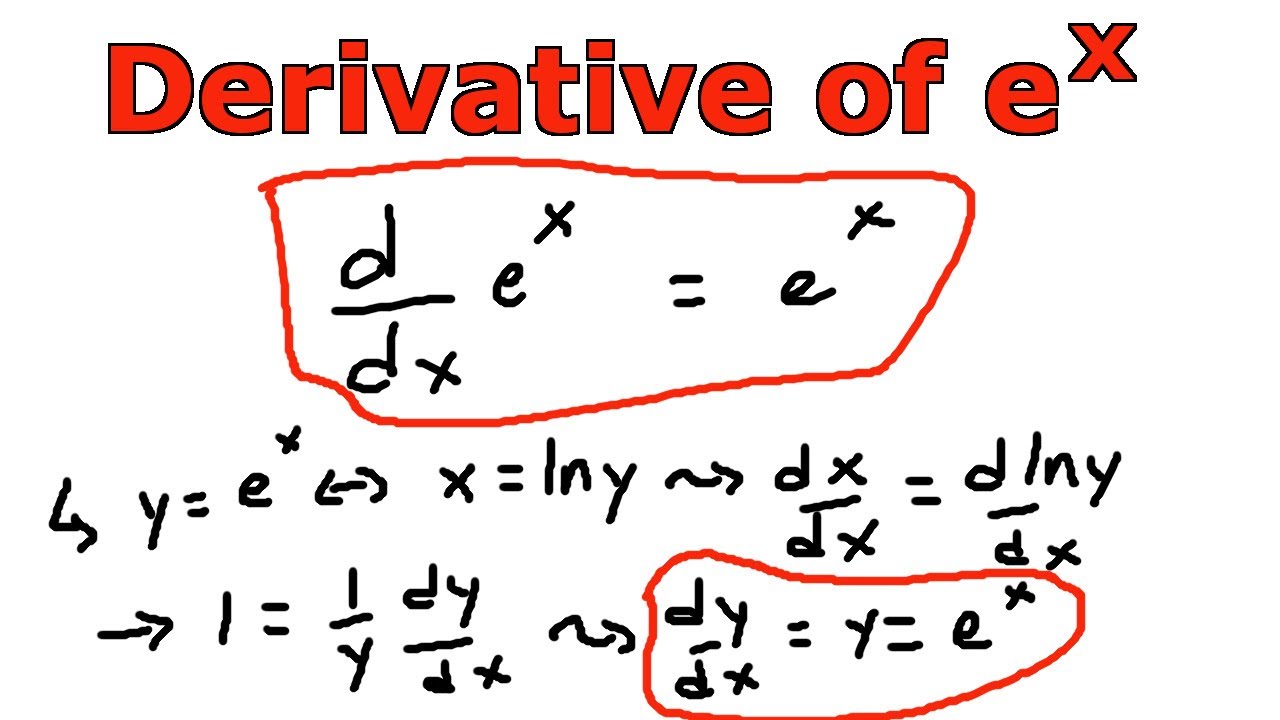


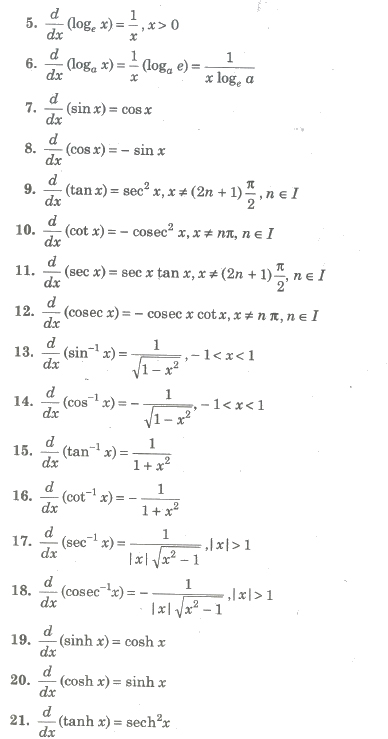





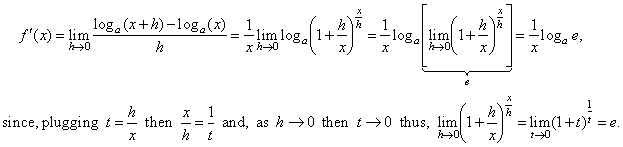






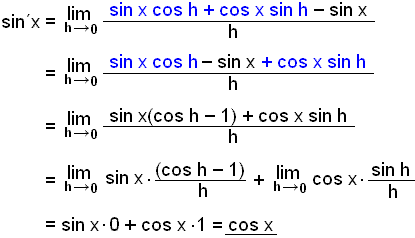

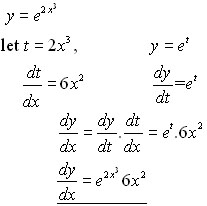

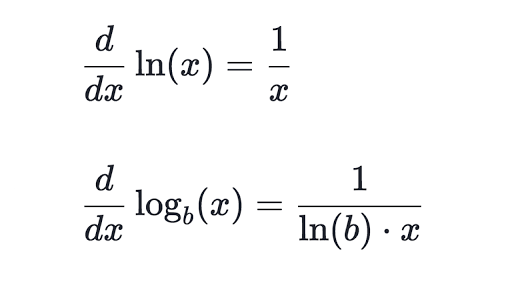




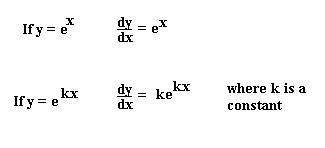


.gif)