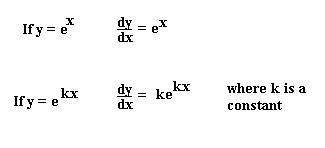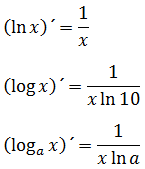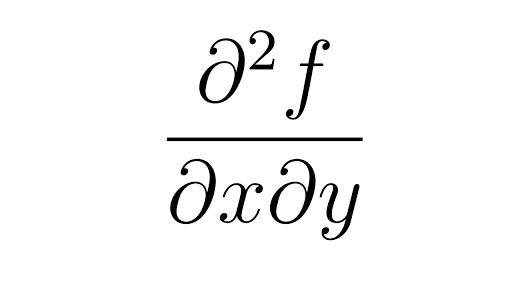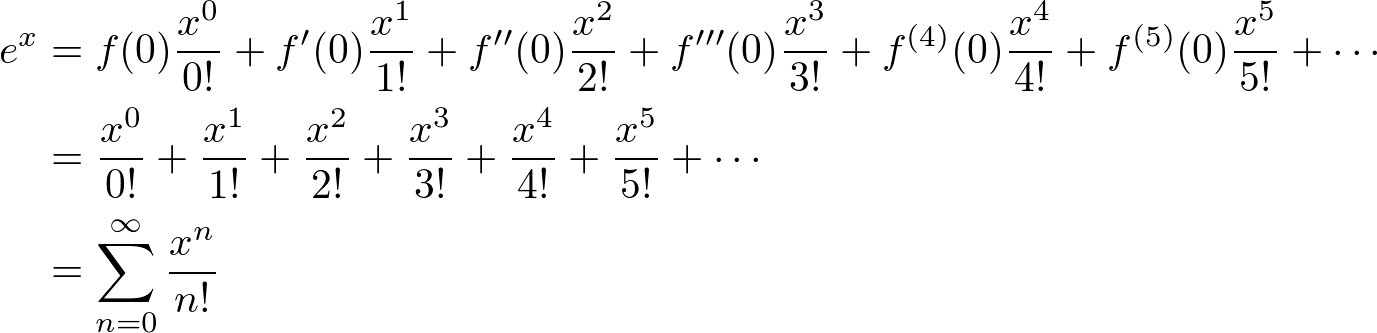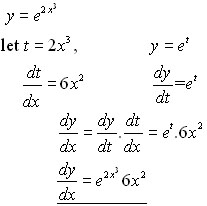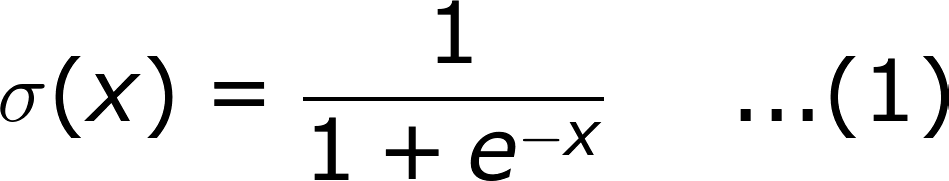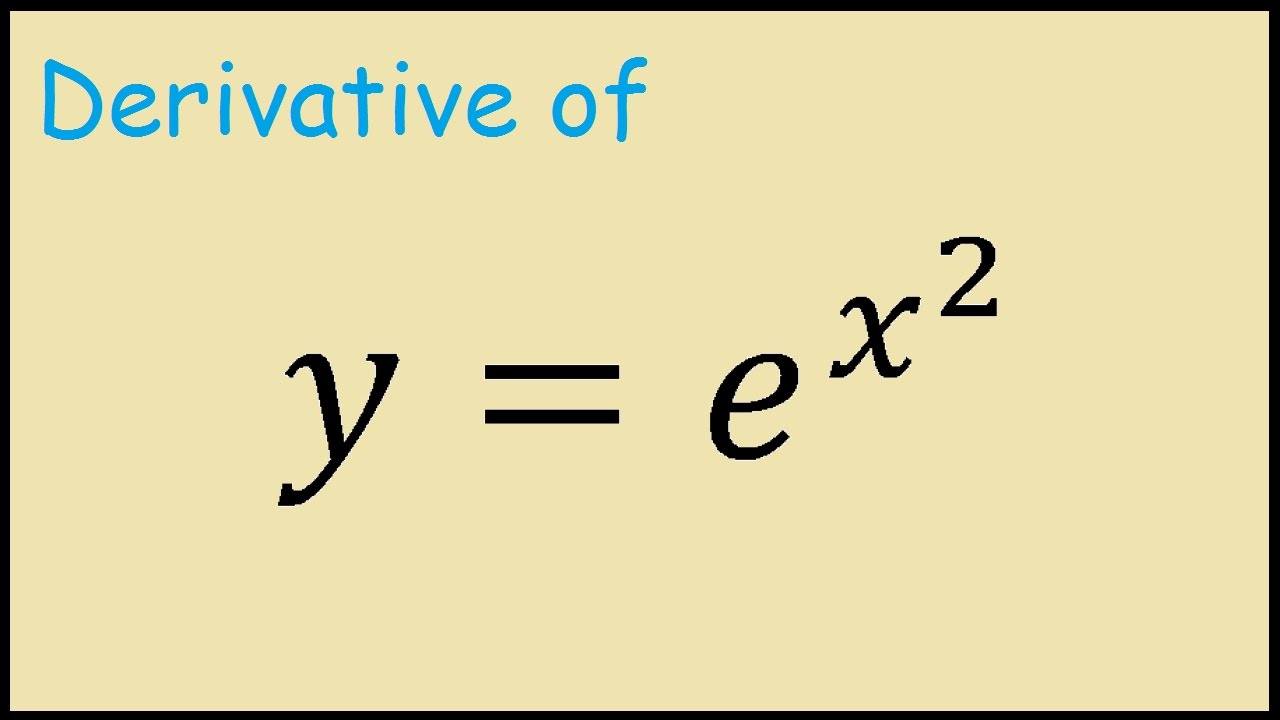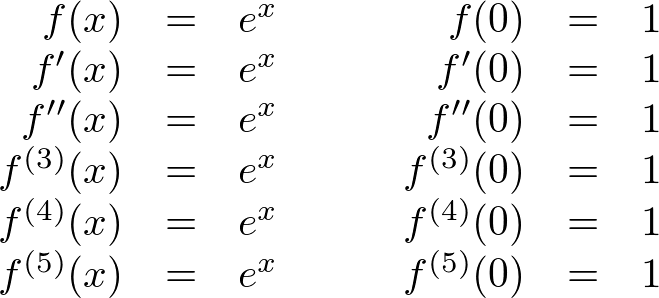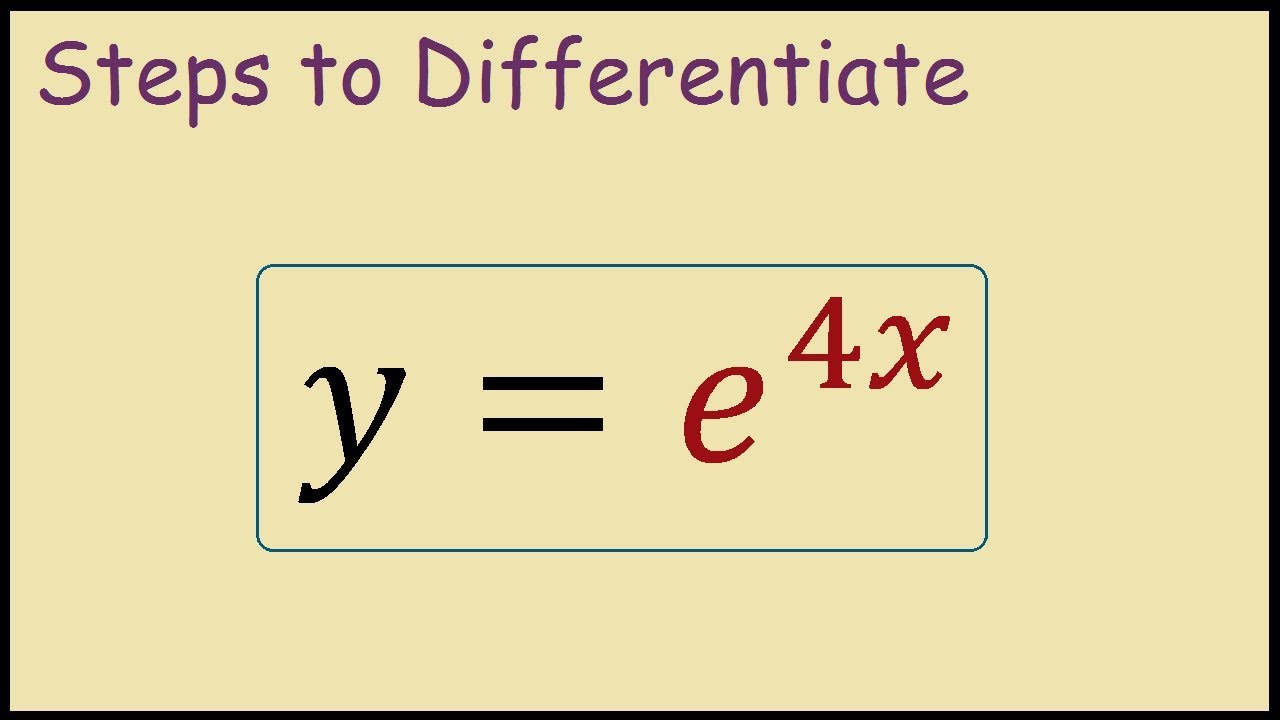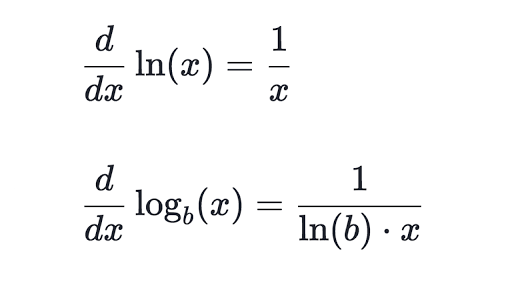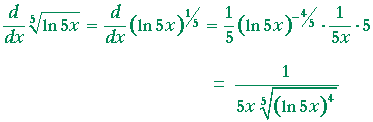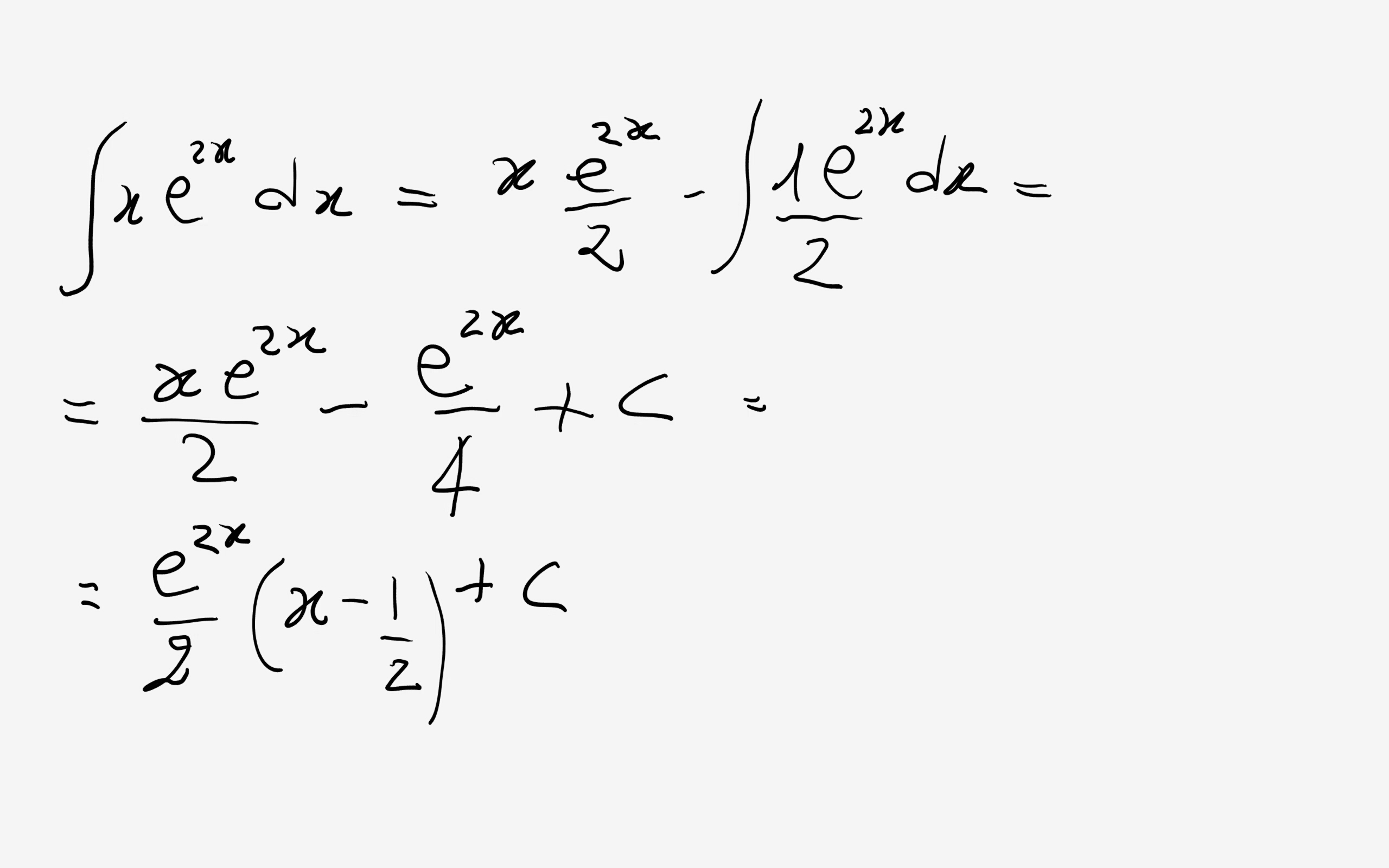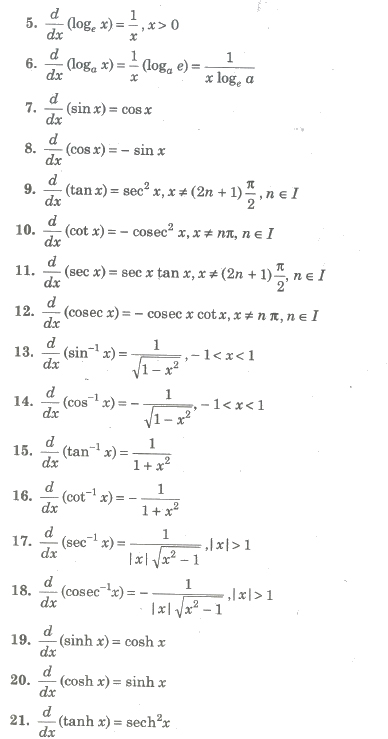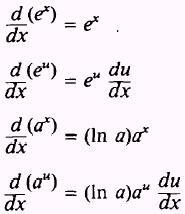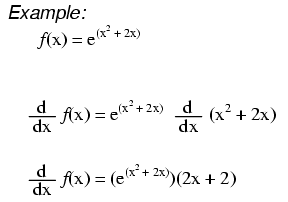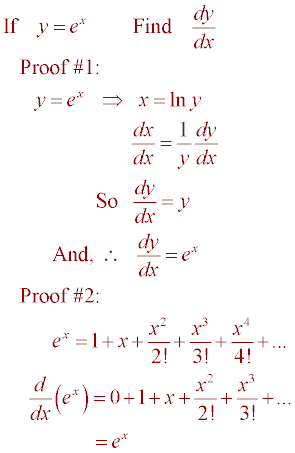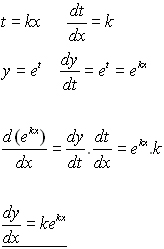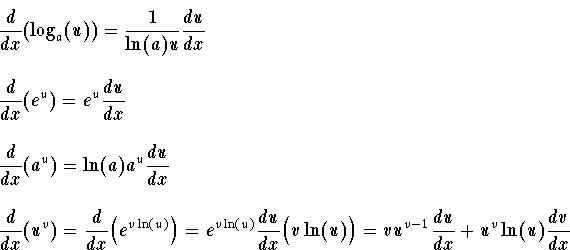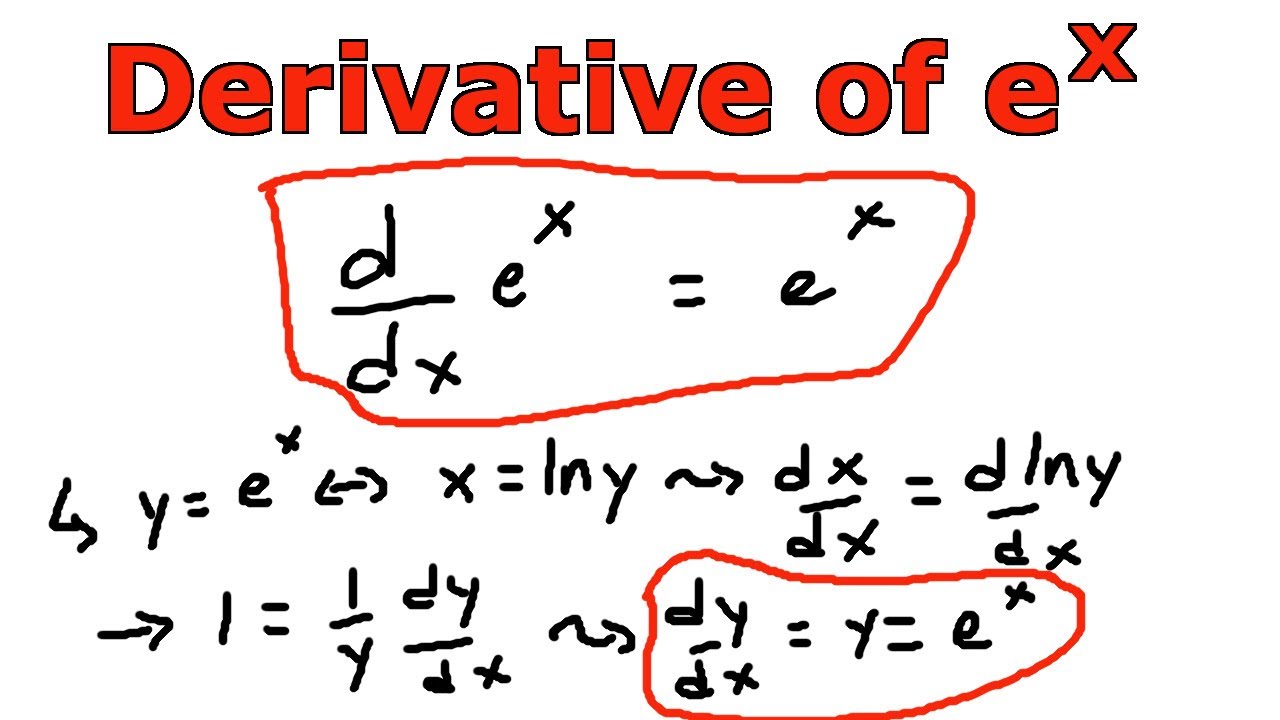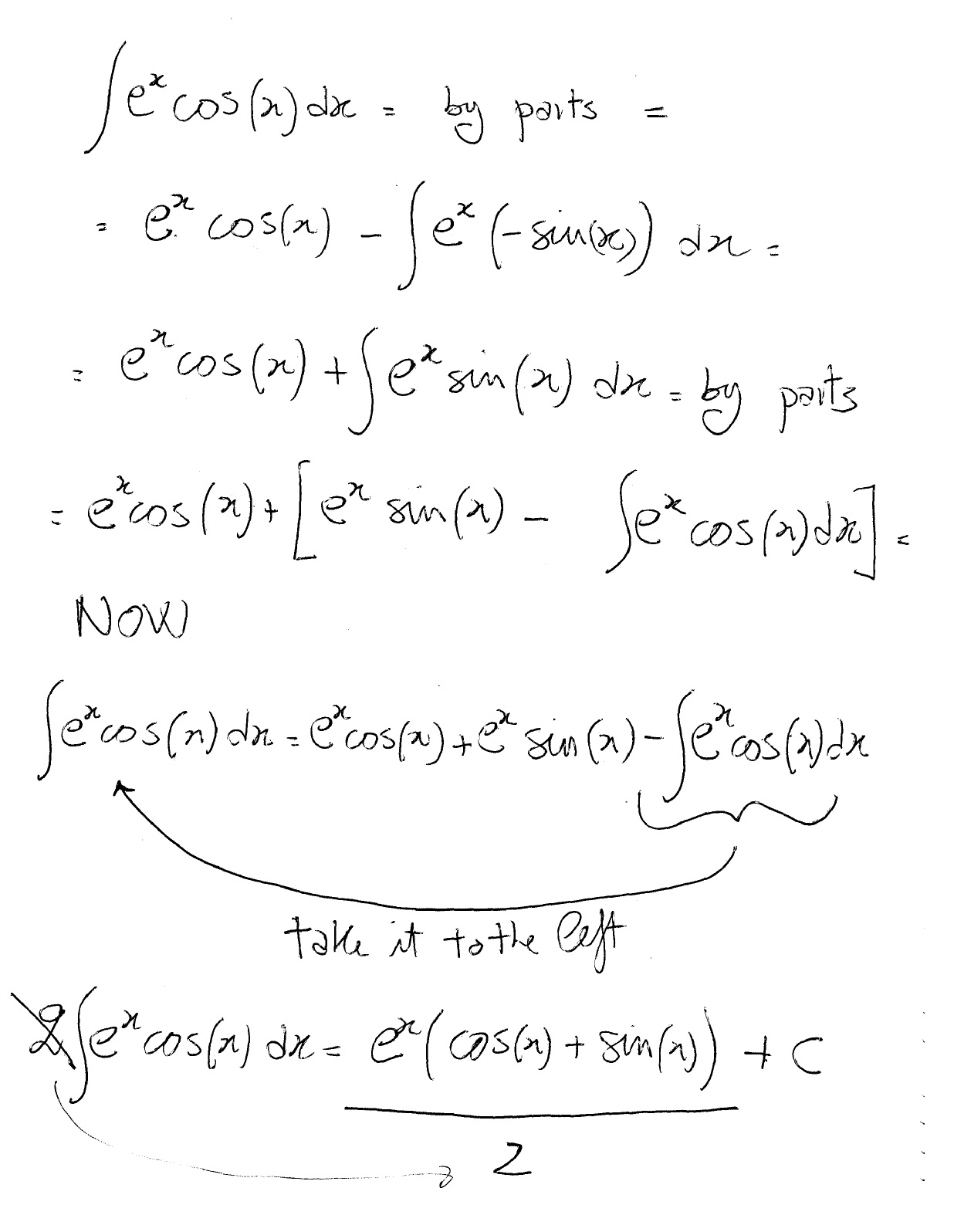Derivative Of Ex Formula
Derivatives Of Logarithmic And Exponential Functions W3spoint
www.w3spoint.com
Exponentials And Logarithms Maths A Level Revision
revisionmaths.com
Integration By Parts Formula Derivation Ilate Rule And Examples
byjus.com
Calculus Derivative Of The Natural Log Ln Solutions Examples Videos
www.onlinemathlearning.com
Solutions Of Tenth Homework
studylib.net
Ex 13 2 7 For Constants A B Find Derivative Of I X A X B
www.teachoo.com
Type in any function derivative to get the solution steps and graph this website uses cookies to ensure you get the best experience.
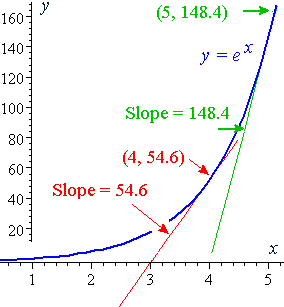
Derivative of ex formula. At a point the derivative is defined to be. Our first contact with number e and the exponential function was on the page about continuous compound interest and number ein that page we gave an intuitive definition of. So right over here the value of the function is 1 and the slope of the tangent line is 1.
The slope of a line like 2x is 2 or 3x is 3 etc. The slope of a constant value like 3 is always 0. The derivative tells us the slope of a function at any point.
Lets just appreciate that. Lets take the example when x 2. Dexdxex what does this mean.
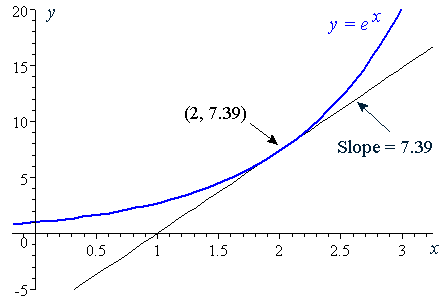
The derivative of a function of a real variable measures the sensitivity to change of the function value output value with respect to a change in its argument input value. The slope of the tangent line at any point here is equal to the value of the function. It means the slope is the same as the function value the y value for all points on the graph.
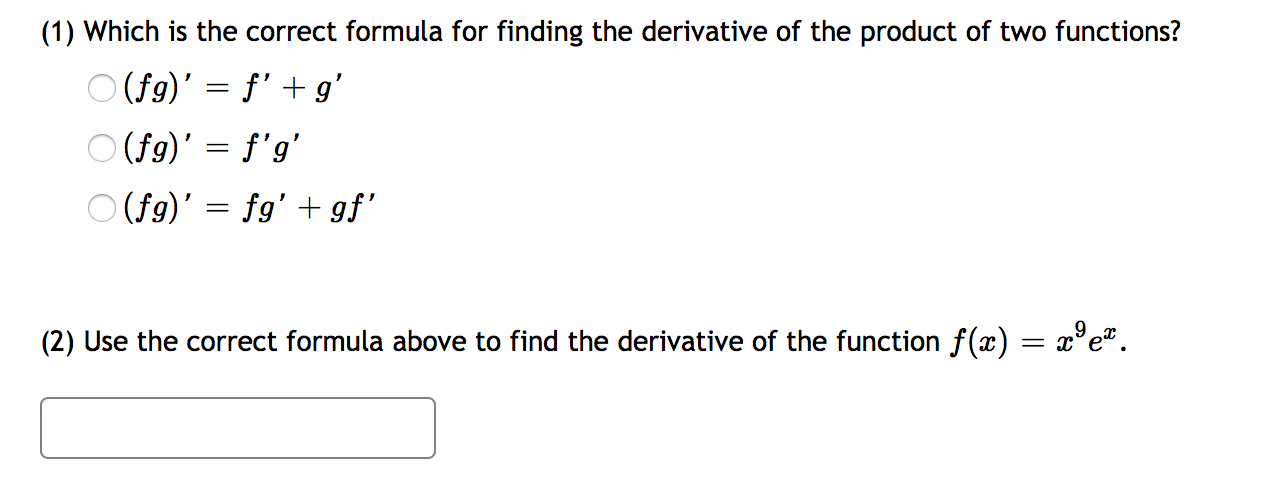
And so what this says is the derivative of e to the x for any x is equal to e to the x. E is the number that where if you take that number to the power of x if you define a function or expression as e to the x its that number where if you take the derivative of that its still going to be e to the x. There are rules we can follow to find many derivatives.
Here are useful rules to help you work out the derivatives of many functions with examples below. At this point the y value is e 2 739. The derivative calculator supports computing first second fifth derivatives as well as differentiating functions with many variables partial derivatives implicit differentiation and calculating rootszeros.
The exponential function is one of the most important functions in calculus. For real numbers c and d a function of the form is also an exponential function since it can be rewritten as. This is part of the graph of y e to the x.
When a derivative is taken times the notation or is used. Note for second order derivatives the notation is often used. The most common ways are and.
Since the derivative of e x is e x then the slope of the tangent line at x 2 is also e 2 739. Free derivative calculator differentiate functions with all the steps. Derivatives are a fundamental tool of calculusfor example the derivative of the position of a moving object with respect to time is the objects velocity.
You can also check your answers. In this page well deduce the expression for the derivative of e x and apply it to calculate the derivative of other exponential functions. Where b is a positive real number not equal to 1 and the argument x occurs as an exponent.
These are called higher order derivatives. As functions of a real variable exponential functions are uniquely characterized by the fact that the growth rate of such a function that is its derivative is directly. In previous lessons or courses youve learned about ways to define e and this could be a new one.
Calculus Graphical Numerical Algebraic 3rd Edition Answers Ch 3 Derivatives Ex 3 3 12e Calculus Math Answers
in.pinterest.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqnye10zfu7n1e5psc 7oyuuimkr8sjknkcqpbj1hdnr3gsgvai Usqp Cau
encrypted-tbn0.gstatic.com
Rbse Solutions For Class 12 Maths Chapter 7 Differentiation Ex 7 1
www.rbsesolutions.com
1
encrypted-tbn0.gstatic.com
Math Scene Derivatives Lesson 5 The Chain Rule
www.rasmus.is
Second Partial Derivatives Article Khan Academy
www.khanacademy.org
L Error Convergence Of Derivatives Computed For F X E X By Download Scientific Diagram
www.researchgate.net
Maclaurin Series Of Exponential Function
www.songho.ca
Maths First Institute Of Fundamental Sciences Massey University
mathsfirst.massey.ac.nz
Sl Formulabooklet
www.slideshare.net
Ap Calculus Review Derivatives Of Inverse Functions Magoosh Blog High School
magoosh.com
Https Www Math Tamu Edu Schlump 17section3 6b Math171 Sol Pdf
Rd Sharma Class 12 Solutions Chapter 11 Differentiation Learn Cbse
www.learncbse.in
Rd Sharma Class 12 Solutions Chapter 11 Differentiation Learn Cbse
www.learncbse.in
Formula Sheet Of Chapter 5 Continuity Differentiability Class 12 Maths Notes
www.learnpick.in
Calculus Graphical Numerical Algebraic 3rd Edition Answers Ch 4 Applications Of Derivatives Ex 4 1 A Plus Topper
www.aplustopper.com
Derivative Exponentials Natural Logarithms Differential Calculus From A Level Maths Tutor
www.a-levelmathstutor.com
Derivative Of The Sigmoid Function By Arunava Towards Data Science
towardsdatascience.com
Derivatives Of Logaithmic Functions
oregonstate.edu
3 6 Derivatives Of Logarithmic Functions In This Section We Use Implicit Differentiation To Find The Derivatives Of The Logarithmic Functions And In Ppt Download
slideplayer.com
Implicit Differentiation Examples Formula Video Lesson Transcript Study Com
study.com
Derivative Of Y E X 2 Youtube
www.youtube.com
Maclaurin Series Of Exponential Function
www.songho.ca
How To Differentiate E 4x Chain Rule Youtube
www.youtube.com
6 Derivative Of The Exponential Function
www.intmath.com
Differentiating Logarithmic Functions Review Article Khan Academy
www.khanacademy.org
Solved Euler S Derivation Of E Ix Cos X I Sin X Is Ea Chegg Com
www.chegg.com
Differentiation Of Exponential And Logarithmic Functions
www.cliffsnotes.com
Chapter 30 Derivatives Rd Sharma Solutions For Class 11 Commerce Mathematics Cbse Topperlearning
www.topperlearning.com
Natural Logarithm Wikipedia
en.wikipedia.org
Derivatives Of Exponential And Logarithmic Functions An Approach To Calculus
themathpage.com
2
Chain Rule Wikipedia
en.wikipedia.org
Answered 1 Which Is The Correct Formula For Bartleby
www.bartleby.com
Exponen Dan Logaritma
www.slideshare.net
Derivative Of The Natural Logarithm
oregonstate.edu
How Do You Integrate Xe 2x Dx Socratic
socratic.org
Finding The Derivative Of Log X Video Lesson Transcript Study Com
study.com
Derivative Rules
www.mathsisfun.com
Implicit Differentiation
www.math.ucdavis.edu
Cbse Notes Class 12 Maths Differentiation Aglasem Schools
schools.aglasem.com
And Q 1 P Derive The Formula E X 2 1 Q P Chegg Com
www.chegg.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcrlw5wx6qxsllz2r9p3fgzffnje5hqap6knkskthxk8e15jx7e4 Usqp Cau
encrypted-tbn0.gstatic.com
Integration Formula
Solved 1 Find The Hundredth Derivative Of P X X 25 Chegg Com
www.chegg.com
Derivative Of Constants To Variable Powers
www.tpub.com
2
Differentiation Formulas Rules Basic Trig Full List Teachoo
www.teachoo.com
6 Derivative Of The Exponential Function
www.intmath.com
Directional Derivative
math.info
Ahmad Badary
ahmedbadary.github.io
Https Www Studocu Com Sg Document National University Of Singapore Engineering Calculus Practical Ma1511 1920s1 Rev Ex 1 Partial Derivatives 7424362 View
Derivatives Of Power Functions Of E Calculus Reference Electronics Textbook
www.allaboutcircuits.com
2
Calculus Exponential Derivatives Examples Solutions Videos
www.onlinemathlearning.com
Lesson 52 Derivatives Of Exponential Functions
www.pleacher.com
Derivative Exponentials Natural Logarithms Differential Calculus From A Level Maths Tutor
www.a-levelmathstutor.com
Supplementary Note Variance Variance Probability Density Function
www.scribd.com
Maclaurin Series Of Exponential Function
www.songho.ca
Finding The Derivative Of Log X Video Lesson Transcript Study Com
study.com
Find The Second Order Derivative Of E3x Sin 4x Explain In Great Detail Mathematics Topperlearning Com J10h42dd
www.topperlearning.com
Curvature And Radius Of Curvature
www.math24.net
Maths First Institute Of Fundamental Sciences Massey University
mathsfirst.massey.ac.nz
2
Partial Derivative Examples Math Insight
mathinsight.org
Solved Find The Derivative Using The Appropriate Differen Chegg Com
www.chegg.com
Function And Relation Library
www.mathnstuff.com
Derivative Calculator Wolfram Alpha
www.wolframalpha.com
Leibniz Formula
www.math24.net
Pdf On Accuracy Of Derivatives On Uniform Grids Revised
www.researchgate.net
The Derivative
www.sosmath.com
Calculus Exponential Derivatives Examples Solutions Videos
www.onlinemathlearning.com
Rbse Solutions For Class 11 Maths Chapter 10 Limits And Derivatives Ex 10 3 Rbsesolutionsforclass11maths Rbsesolutions Class1 Math Maths Syllabus Solutions
in.pinterest.com
Rbse Solutions For Class 12 Maths Chapter 7 Differentiation Ex 7 1
www.rbsesolutions.com
6 Derivative Of The Exponential Function
www.intmath.com
What Is The General Formula To Find Nth Derivative Of A Function Quora
www.quora.com
Lesson 52
www.pleacher.com
Copyright C Cengage Learning All Rights Reserved 11 Techniques Of Differentiation With Applications Ppt Download
slideplayer.com
8 2 Integration By Parts
studylib.net
Integral Of E X 2 Fasrwhy
fasrwhy438.weebly.com
Integration By Parts
www.mathsisfun.com
Calculus Graphical Numerical Algebraic 3rd Edition Answers Ch 5 The Definite Integral Of Derivatives Ex 5 5 A Plus Topper
www.aplustopper.com
Derivative Of E X Using The Inverse Function Method Youtube
www.youtube.com
Lecture 3 The Natural Exponential Function F X Exp X E X Y Exp X If And Only If X Ln Y Pdf Free Download
docplayer.net
Formula Sheet Of Chapter 5 Continuity Differentiability Class 12 Maths Notes
www.learnpick.in
Ex 13 2 4 Find Derivative From First Principle I X3 27
www.teachoo.com
The Derivative Of E To X Formula And Example Lunlun Com
lunlun.com
5 4 Exponential Functions Differentiation And Integration The Inverse Of F X Ln X Is F 1 E X Therefore Ln E X X And E Ln X X Solve For Ppt Download
slideplayer.com
Quotient Rule Wikipedia
en.wikipedia.org
Derivation Of Variance Of Normal Distribution With Gamma Function Cross Validated
stats.stackexchange.com
2
What Is The Expansion Of Math 1 E X 1 Math Quora
www.quora.com
The Derivative
www.sosmath.com
Moment Generating Function Explained By Aerin Kim Towards Data Science
towardsdatascience.com
Differentiation Formulas Rules Basic Trig Full List Teachoo
www.teachoo.com
How Do You Find The Integral Of E X Cosx Dx Socratic
socratic.org
Rd Sharma Solutions For Class 11 Chapter 30 Derivatives Download Free Pdf Available
byjus.com
Falkenblog Formula For Var Xy
falkenblog.blogspot.com
