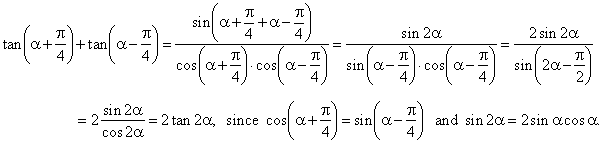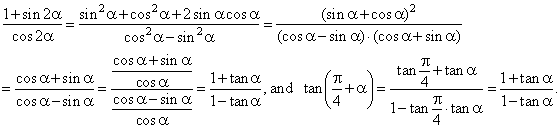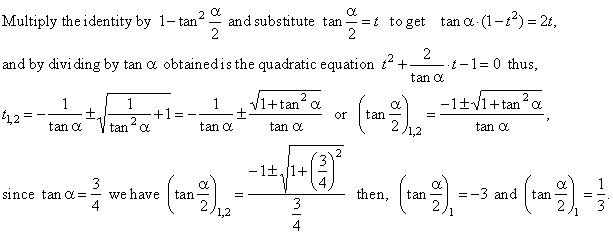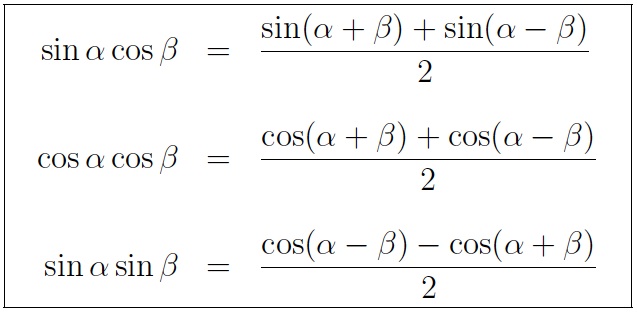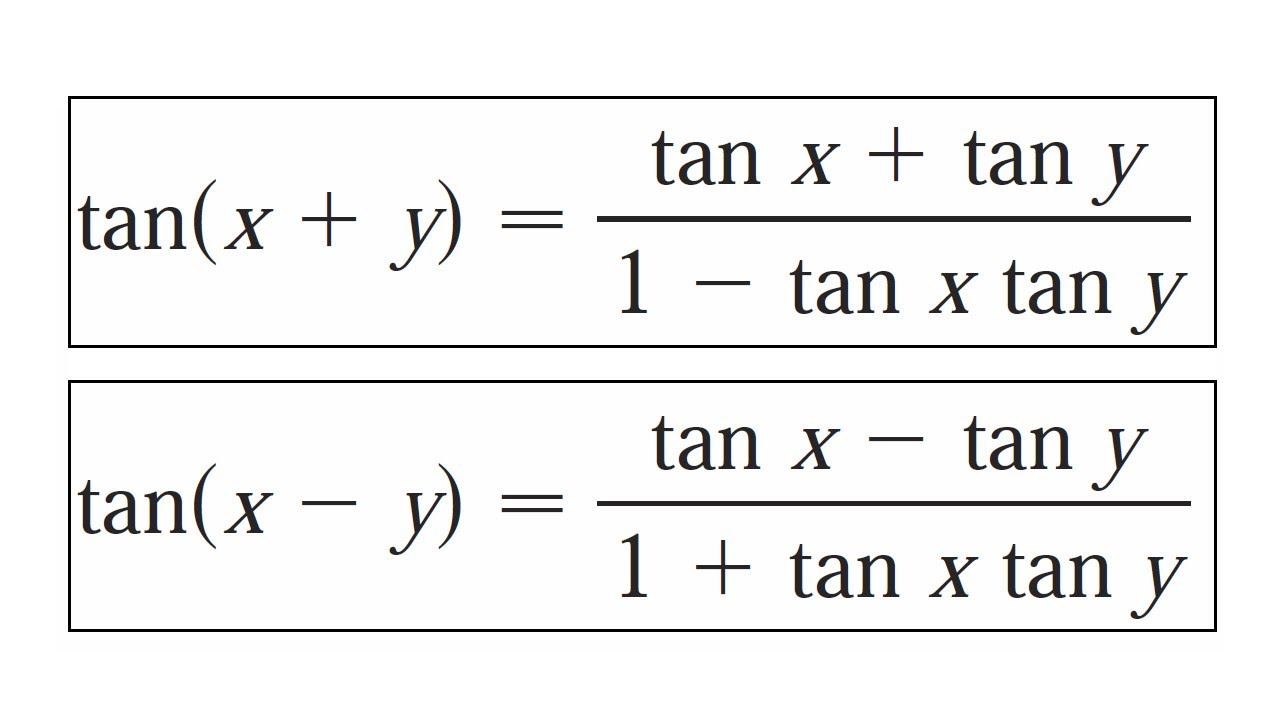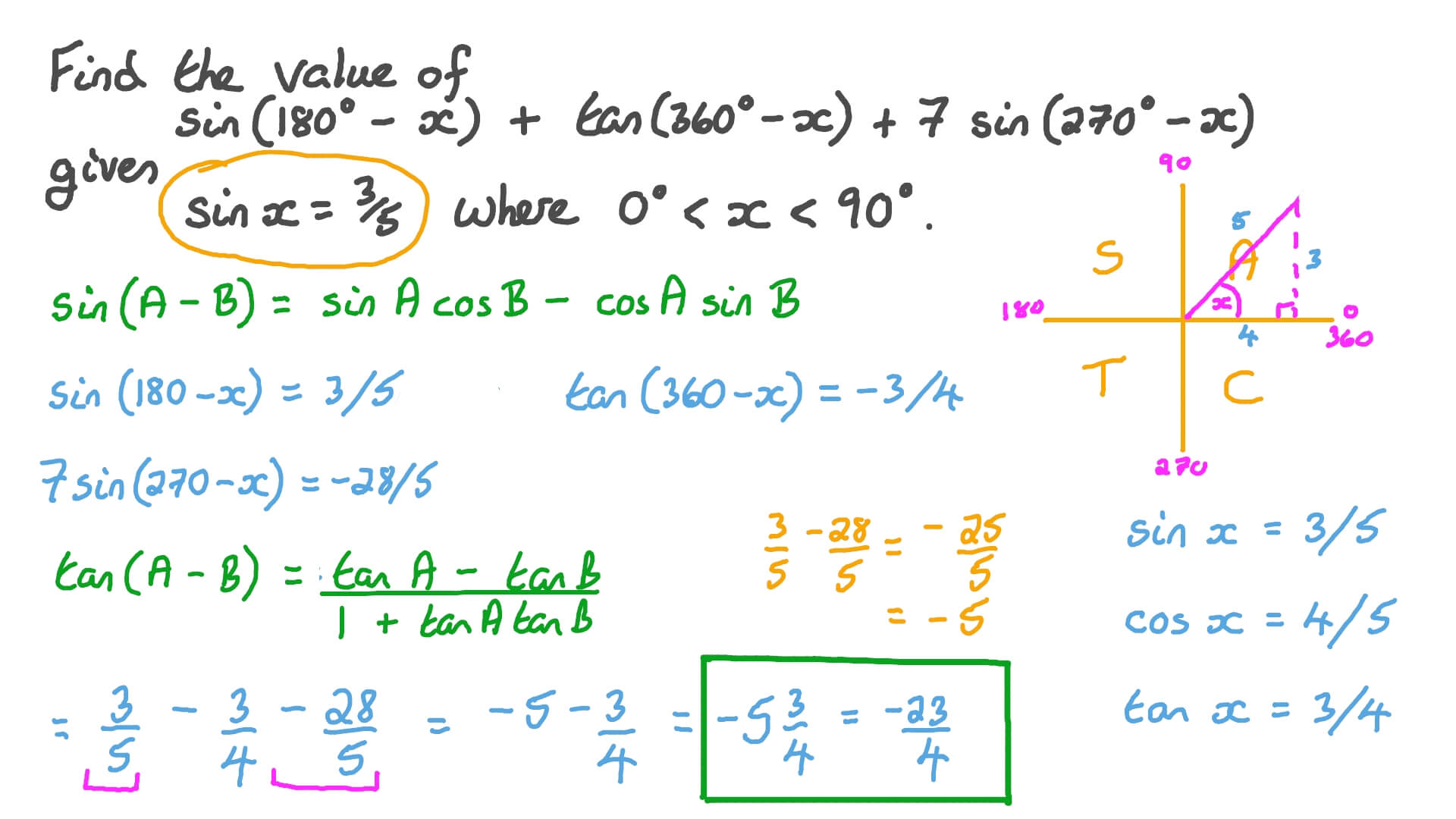Cosab Formula In Terms Of Tan
Rd Sharma Solutions For Class 10 Chapter 5 Trigonometric Ratios Exercise 5 1 Get Pdf For Free
byjus.com
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com
Compound Angle Identity Tan 3x Formula Derivation Youtube
www.youtube.com
Important Trigonometric Identiti
www.pstcc.edu
Solved Verify The Identity Cos A B Cos A Sin B Cot Chegg Com
www.chegg.com
Search Q Sin A B Tbm Isch
Using that fact tan a b sin a bcos a b.
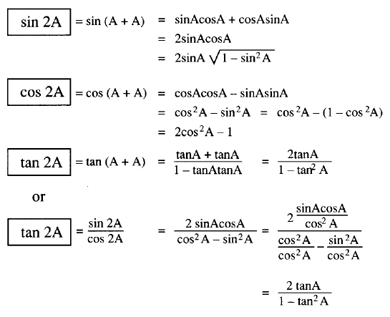
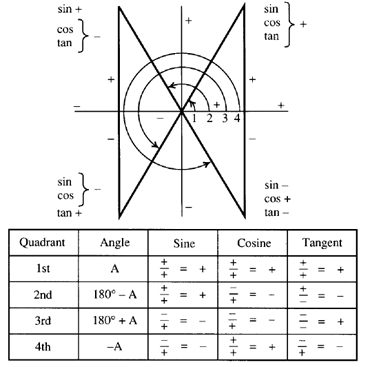
Cosab formula in terms of tan. We know if a is a number or angle then we have cos 2a cos2 a sin2 a. An easy way is to derive it from the two formulas that you have already done. Trigonometric function of cos 2a in terms of tan a is also known as one of the double angle formula.
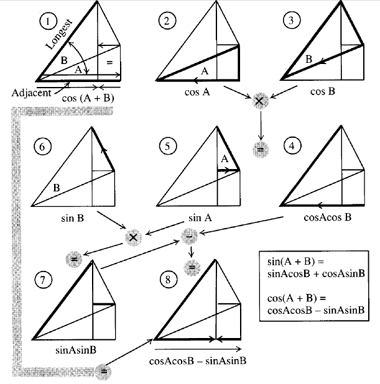
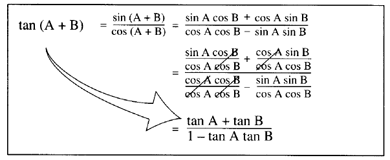
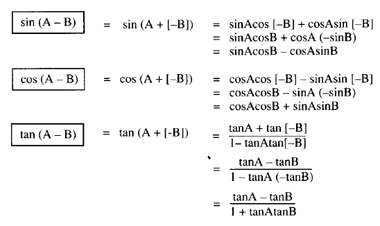
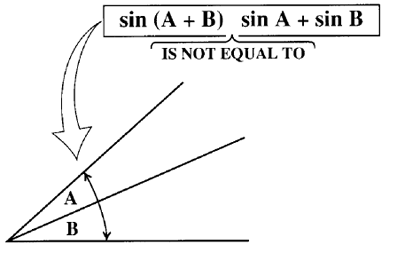
The functions sine cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions. One can also produce them algebraically using eulers formula. Sina b sinacosb cosasinb sinab sinacosbcosasinb cosabcosacosb sinasinb cosa bcosacosbsinasinb.
That youd like to know tanab in terms of tan aand tan brather than all those sines and cosines. In various applications of trigonometry it is useful to rewrite the trigonometric functions such as sine and cosine in terms of rational functions of a new variable tthese identities are known collectively as the tangent half angle formulae because of the definition of tthese identities can be useful in calculus for converting rational functions in sine and cosine to functions of t in. In mathematics the inverse trigonometric functions occasionally also called arcus functions antitrigonometric functions or cyclometric functions are the inverse functions of the trigonometric functions with suitably restricted domainsspecifically they are the inverses of the sine cosine tangent cotangent secant and cosecant functions and are used to obtain an angle from any of.
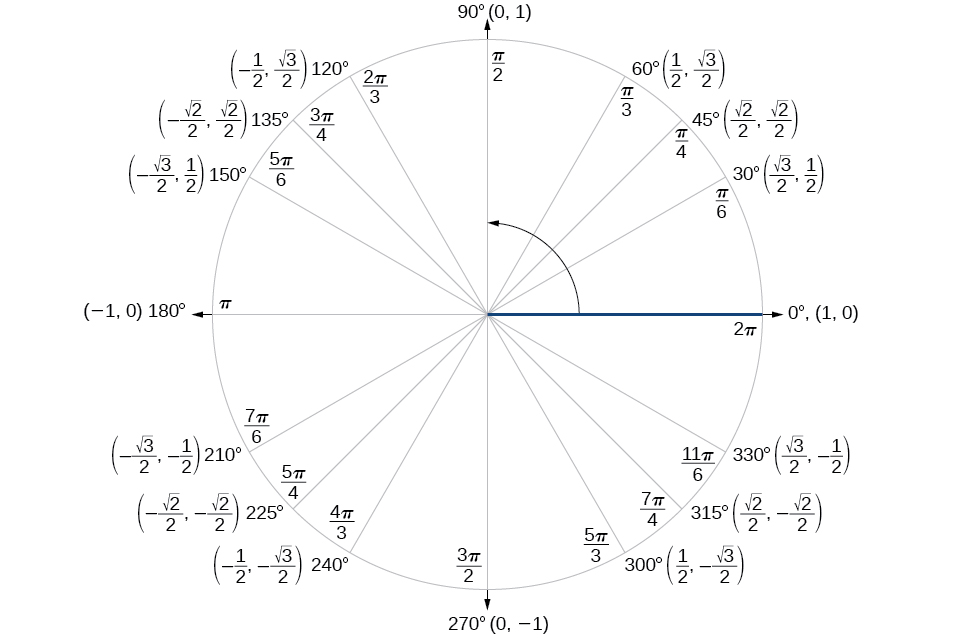
The parentheses around the argument of the functions are often omitted eg sin o and cos o if an interpretation is unambiguously possible. Sum and difference formula sina b sin acosbcos asinbsina b sin acosb cos asinbcosa b cos acosb sin asinbcosa b cos acosbsin asinbtana b tan atanb 1 tan atanb tana b tan a tanb 1tan atanb double angle formula. The sum and difference formulas allow expanding the sine the cosine and the tangent of a sum or a difference of two angles in terms of sines and cosines and tangents of the angles themselves.
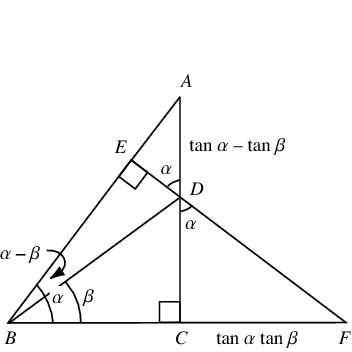
A complete geometric derivation of the formula for tan a b is complicated. The numerator and denominator contain sines and cosines so if you divide by cosines youd expect to end up with sines or perhaps sines over cosines. In any angle the tangent is equal to the sine divided by the cosine.
Their usual abbreviations are sino coso and tano respectively where o denotes the angle.
What Is The Formula Of Cot A B Quora
www.quora.com
Important Trigonometric Identiti
www.pstcc.edu
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com
Expressing Sin X And Cos X In Terms Of Tan X Youtube
www.youtube.com
How Is Tan A B Tana Tanb 1 Tanatanb Quora
www.quora.com
Tangent Half Angle Formula Wikipedia
en.wikipedia.org
Solved I A B Formulas For Cos A B And Sin A B Ea Chegg Com
www.chegg.com
Trigonometric Identities Ppt Video Online Download
slideplayer.com
How To Verify Cos A B Sin A B 1 Cotacotb Cota Cotb Quora
www.quora.com
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com
I Want To All Formula Of Trigonometric Brainly In
brainly.in
44 If Tan A 1 Cos B Sinb Find Tan 2 A In Terms Of Tan B Youtube
www.youtube.com
A 7 1 Trigonometric Identities Sin I Y And Sin I Y R R So
www.yumpu.com
Sine And Cosine Addition Formulas Solutions Examples Videos
www.onlinemathlearning.com
Tangent Half Angle Formula Wikipedia
en.wikipedia.org
Summary Of Trigonometric Identities
www2.clarku.edu
Tangent Half Angle Formula Wikipedia
en.wikipedia.org
New Page 1
www.pstcc.edu
Example 12 Express Cos A Tan A And Sec A In Terms Of Sin A
www.teachoo.com
Interconversion Between Inverse Trigonometric Ratios What Is Interconversion Between Inverse Trigonometric Ratios Examples Solutions Cuemath
www.cuemath.com
Trigonometric Functions Of Double Angles Expressed By The Tangent Function Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities Examples
www.nabla.hr
Express All The Trigonometric Ratios In Terms Of Tan 8 With Calculations Brainly In
brainly.in
New Page 1
www.pstcc.edu
What Are The Formulas Of Cos 2x Quora
www.quora.com
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com
Solved Based On Euler S Formula E I Cos I Sin Where Chegg Com
www.chegg.com
Cbse 10 Math Cbse Introduction To Trigonometry Ncert Solutions
www.careerlauncher.com
Half Angle And Double Angle Formulas Wyzant Resources
www.wyzant.com
Sin A Sin B Cos A Cos B Tan A B 2 Youtube
www.youtube.com
Trigonometry Formula
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcsknjfedd3db9ix7b7kwsjnfhkbb67tnw Yk27 P Gsfqrxg1g Usqp Cau
encrypted-tbn0.gstatic.com
Relating Trigonometric Functions Trigonometry Socratic
socratic.org
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com
Example 12 Simplify Tan 1 A Cos X B Sin X B Cos X
www.teachoo.com
Solved Verify The Identity Sin A B Sin A Cos B 1 Cot A Chegg Com
www.chegg.com
Tangent Identities
www.cliffsnotes.com
Trig Addition Formulae Ppt Download
slideplayer.com
Solve Sin Tan 1 X Inverse Trigonometry Teachoo Miscellaneous
www.teachoo.com
Proof Of The Cosine Angle Addition Identity Video Khan Academy
www.khanacademy.org
Trigonometric Functions Of Double Angles Expressed By The Tangent Function Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities Examples
www.nabla.hr
Tangent Half Angle Formula Wikipedia
en.wikipedia.org
How To Use The Excel Tan Function Exceljet
exceljet.net
Image Result For Compound Angle Formula Formula Math Compounds
www.pinterest.com
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com
Inverse Trigonometric Functions Wikipedia
en.wikipedia.org
Example 5 Express Tan 1 Cos X 1 Sin X Chapter 2 Inverse
www.teachoo.com
Important Trigonometric Identiti
www.pstcc.edu
Tangent Half Angle Formula Wikipedia
en.wikipedia.org
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com
Math Analysis Honors Math Sheets M Modeling A Again T
studyres.com
Example 5 Express Tan 1 Cos X 1 Sin X Chapter 2 Inverse
www.teachoo.com
What Is The Formula Of Cot A B Quora
www.quora.com
Cbse 10 Math Cbse Introduction To Trigonometry Ncert Solutions
www.careerlauncher.com
Ex 8 4 1 Express Sin A Sec A And Tan A In Terms Of Cot A
www.teachoo.com
Formulas Formulae For Class Xi Math
www.slideshare.net
Summary Of Trigonometric Identities
www2.clarku.edu
Calcu Fundamental Identities
www.calcu-us.appspot.com
2
14 2 Trigonometric Identities
mathonweb.com
Summary Of Trigonometric Identities
www2.clarku.edu
Given Sina And Cosb Find Tan A B Test Q5 Youtube
www.youtube.com
Trigonometric Functions Of Double Angles Expressed By The Tangent Function Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities Examples
www.nabla.hr
Summary Of Trigonometric Identities
www2.clarku.edu
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com
Misc 4 Prove Sin 1 8 17 Sin 1 3 5 Tan 1 77 36 Miscellaneous
www.teachoo.com
How To Prove Tan A B Basic Formula Quora
www.quora.com
Summary Of Trigonometric Identities
www2.clarku.edu
Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube
www.youtube.com
Section 4 Sine And Cosine Rule
www.cimt.org.uk
Sine And Cosine Addition Formula Examples Solutions Videos Worksheets Activities
www.onlinemathlearning.com
Trigonometric Identities 3 Sample Problems
studyres.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcsr4 S2mwqyyvcchtc3gopfh7qymvafk7mrnbovstzrqefeajoc Usqp Cau
encrypted-tbn0.gstatic.com
Trig Addition Formulae Ppt Download
slideplayer.com
Sin Alpha Sin Beta M And Cos Alpha Cos Beta N Find Tan Alpha Beta 2 Mathematics Topperlearning Com Wlcziqq
www.topperlearning.com
Trigonometric Identity Tan X Y Proof Youtube
www.youtube.com
Solved This Question 1 Pt Verify The Identity Sin A B Chegg Com
www.chegg.com
How To Prove That Math Tan A B Frac Tan A Tan B 1 Tan A Tan B Math Quora
www.quora.com
14 2 Trigonometric Identities
mathonweb.com
Analytic Trigonometry
xaktly.com
New Page 1
www.pstcc.edu
Summary Of Trigonometric Identities
www2.clarku.edu
Cbse 10 Math Cbse Introduction To Trigonometry Ncert Solutions
www.careerlauncher.com
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com
Video Using Cofunctions Identities And Periodic Identities To Evaluate Expressions Nagwa
www.nagwa.com
Ex 2 2 8 Chapter 2 Class 12 Inverse Tan 1 Cos X Sin X
www.teachoo.com
Important Trigonometric Identiti
www.pstcc.edu
Solved I Don T Know How To Solve Both Of The Questions C Chegg Com
www.chegg.com
7 3 Sum And Difference Identities Mathematics Libretexts
math.libretexts.org
Trig Addition Formulae Ppt Download
slideplayer.com
How To Use The Excel Cos Function Exceljet
exceljet.net
Trigonometric Addition Formulas From Wolfram Mathworld
mathworld.wolfram.com
What Are Sine Cosine And Tangent
www.quickanddirtytips.com
New Page 1
www.pstcc.edu
Sum And Difference Identities Formulas Sine Cosine Tangent Degrees Radians Trigonometry Youtube
www.youtube.com
Solved Verify The Identity Cos A B Cos A Sin B Cot Chegg Com
www.chegg.com
Addition Formula Question Expressing Function In Terms Of Rsin A B Math Help Forum
mathhelpforum.com
New Page 1
www.pstcc.edu
