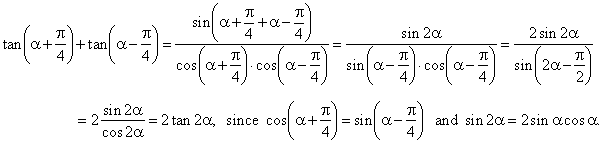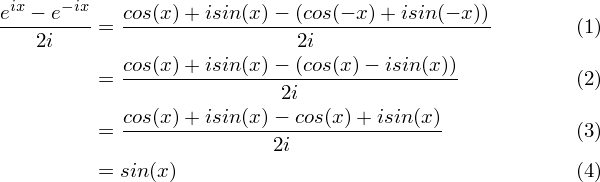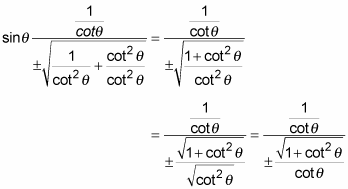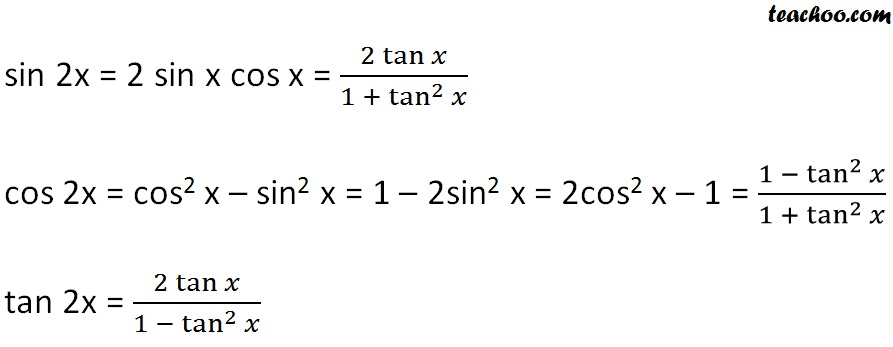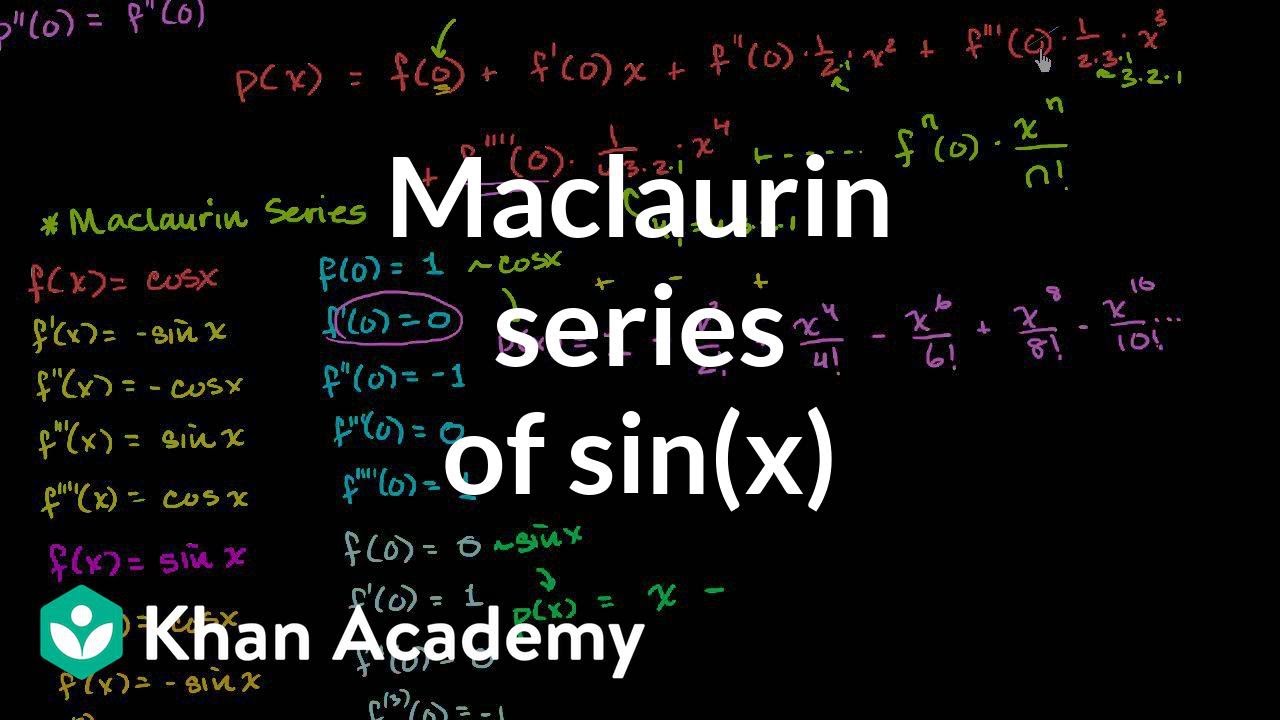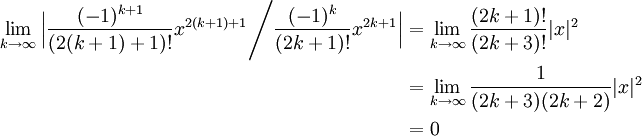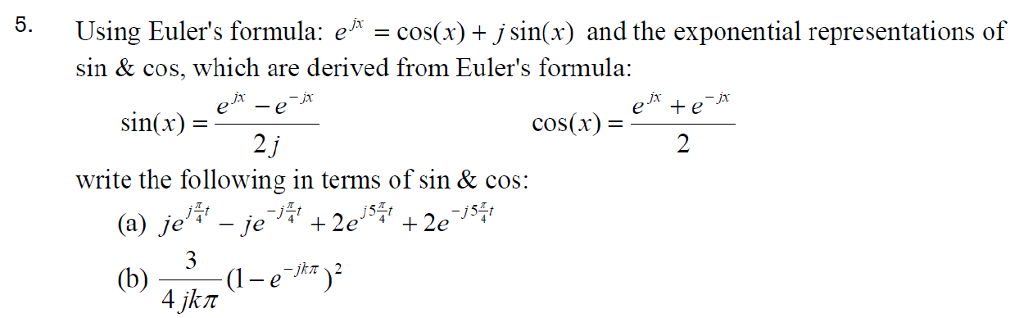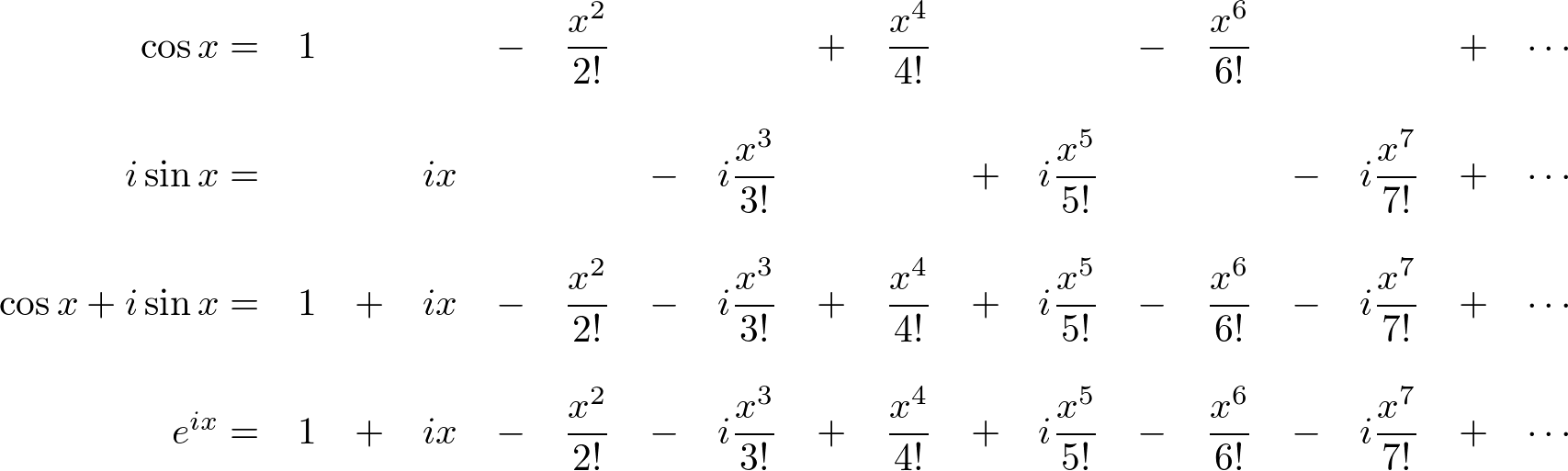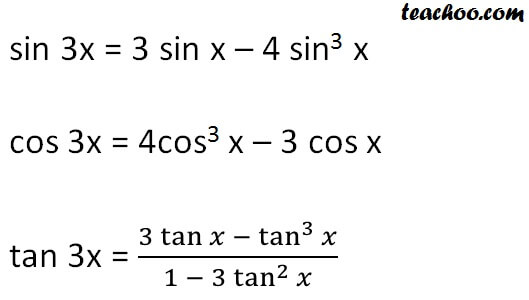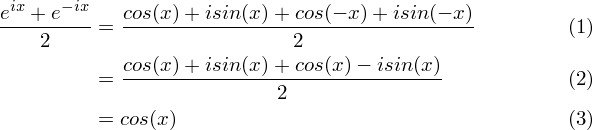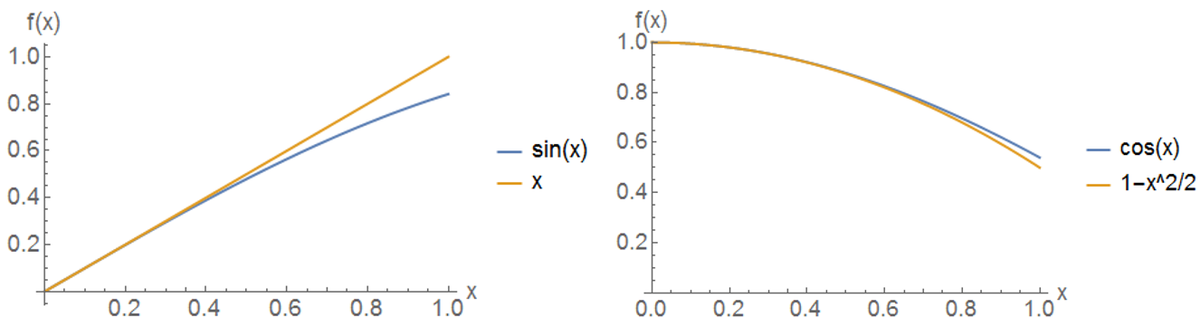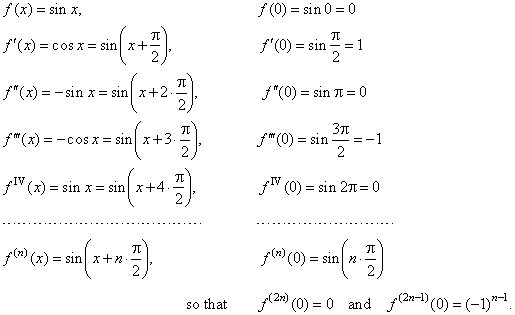Cos X Formula In Terms Of Sin

What Is The Value Of Cos3x In Term Of Cosx Quora
www.quora.com

Summary Of Trigonometric Identities
www2.clarku.edu

Solved Verify The Identity Sin X Sin X Cos X Sin Chegg Com
www.chegg.com

Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube
www.youtube.com

Integrate Sin 22x Cos 22x
www.petervis.com

4 06 Graphs Of Sine And Cosine
www.andrews.edu

The same lower case letter denotes an edge of the triangle and.

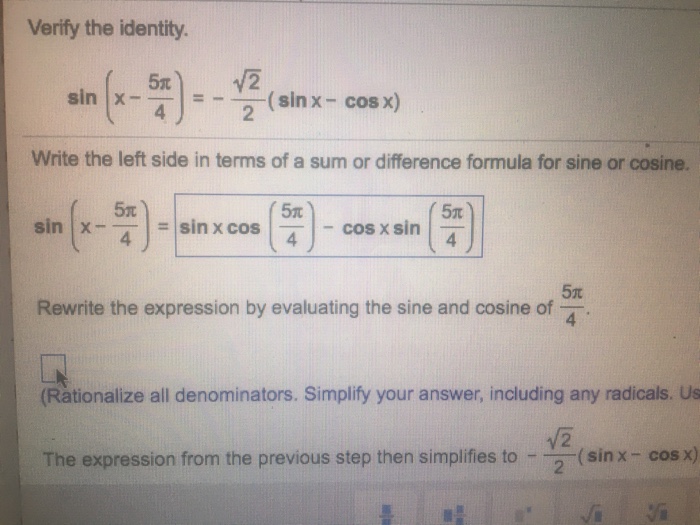
Cos x formula in terms of sin. Introduction to integral of sine formula with introduction and mathematical proof to prove the integration of sinx is equal to cosxc in calculus. Sinu v sinucosv cosusinv cosu v cosucosv sinusinv sin3x sin2xx sin2xcosx cos2xsinx from the identities above we have. Sin and cos formulas are given in this article.

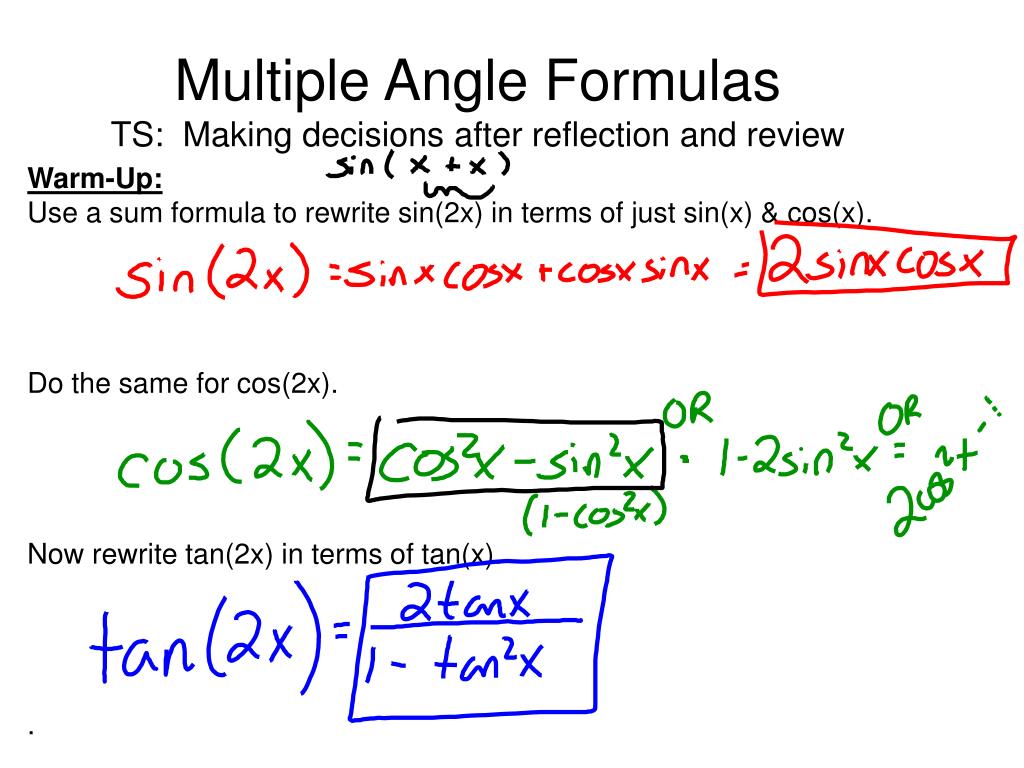
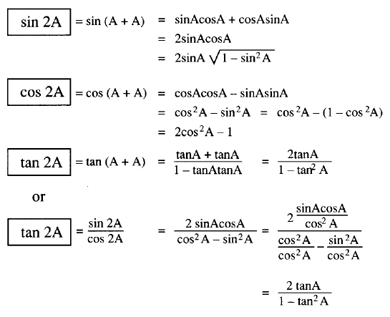
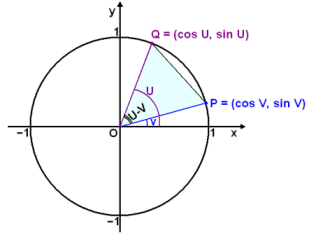
Sino tano and 1 are the heights to the line starting from the x axis while coso 1 and coto are lengths along the x axis starting from the origin. Sin2x 2sinxcosx cos2x cos2x sin2x hence we have. In this section the same upper case letter denotes a vertex of a triangle and the measure of the corresponding angle.

We know that cos 2xcos2 x sin2 x cos 2x1 sin2 x sin2 x cos 2x12sin2 x by this 1 cos 2x 2sin2 x putting xx2we get 1 cos x 2sin2 x2 and this is the formula of 1 cos x. For purely imaginary values z ix where x is real we. Formula of cos 4x ie you need the angle in x form since we know cos 2x cos2x sin2x sin2x 2sinxcosx by applying the above.

Sin3x 2sinxcosxcosx cos2x sin2xsinx 2sinxcos2x sin3x sinxcos2x 3sinxcos2x sin3x 3sinx1 sin2x. These equations which also are called eulers formulas can be used to determine the values of cos z and sin z for complex z. You can find basic trigonometry formulas identities triple angle and double angle formulas.

Where e is the base of the natural logarithm i is the imaginary unit and cos and sin are the trigonometric functions. Sin3x cos3x and tan3x all the three formulas are very important in trigonometryalready in previous article i explained how to derive the formula for sin3x. E iz cos z i sin z.

From this formula expressions can be obtained for sin x and cos x in terms of the exponential functions of a purely imaginary argument. So cos 4x cos 22x cos2 2x sin2 2x cos 2x2 sin 2x2 cos2x sin2x 2 2sinxcosx2 cos4 x. It can be rewritten in terms of two addition identities.

Ex 3 3 19 Prove Sin X Sin 3x Cos X Cos 3x Tan 2x
www.teachoo.com

How To Express Sin X In Terms Of Cot X Quora
www.quora.com

Lesson 24 Double Angle Half Angle Identities Ppt Video Online Download
slideplayer.com

Integrate Sin X Cos X 9 16 Sin 2x Mathematics Topperlearning Com Or6f06mm
www.topperlearning.com

Integration Calculus Notes
www.learnpick.in

14 2 Trigonometric Identities
mathonweb.com

Fourier Sine And Cosine Series
www.sosmath.com

Math34 Trigonometric Formulas
www.slideshare.net

Trigonometric Functions Of Double Angles Expressed By The Tangent Function Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities Examples
www.nabla.hr

Exponential Functions Vs Trigonometric And Hyperbolic Functions
www.efunda.com

What Is The Formula Of 1 Cosx Quora
www.quora.com

Euler S Formula Wikipedia
en.wikipedia.org

How To Rewrite Math Sin 4 X Math So That It Involves Only The First Power Of Cosine Quora
www.quora.com

Properties Of A Inverse Trigonometric Function Tutorsonnet
www.tutorsonnet.com

Euler S Formula
www.ctralie.com

Expressing Sin X And Cos X In Terms Of Tan X Youtube
www.youtube.com

Math34 Trigonometric Formulas
www.slideshare.net

Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcsr4 S2mwqyyvcchtc3gopfh7qymvafk7mrnbovstzrqefeajoc Usqp Cau
encrypted-tbn0.gstatic.com

38 Solved Questions Of Trigonometry For Trigonometric Identities Trigonometric Identities Trigonometry Sci Pi
scipitutor.blogspot.com

How To Express Cos In Terms Of Sin Study Com
study.com

Tangent Half Angle Formula Wikipedia
en.wikipedia.org

Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcso8 U 4tynzyfn8hqcltm8bfcqs4jy7wlwkkw00vruoaif Meh Usqp Cau
encrypted-tbn0.gstatic.com

Express Sine In Terms Of Cotangent Dummies
www.dummies.com

Formula Sin3x 3sinx 4sin 2x In Terms Of Sinx Youtube
www.youtube.com

Solved Find A Formula For The Graph In Terms Of F X Si Chegg Com
www.chegg.com

Inverse Circular Function Study Material For Iit Jee Askiitians
www.askiitians.com

What Are The Formulas Of Sin 2x Quora
www.quora.com

The Circular Trigonometric Functions Let C Be The Circle With The Following Equation X Y 1 Let A Be The Point 1 0 On C Let N Be Any Real Number And P Be The Point On C Obtained By
lawsofemotion.tumblr.com

Answered Prove The Identity Sin 90 X Sin 90 Bartleby
www.bartleby.com

Solved 12 Consider The Following Formula Sin Nx Sin X Chegg Com
www.chegg.com

Transformation Of Cos X To Sin X Via Cos X Frac Pi 2 Sin X Mathematics Stack Exchange
math.stackexchange.com

Trigonometric Identities Ppt Video Online Download
slideplayer.com

The Trigonometric Ratios Of Angl
www.pstcc.edu

7 2 Addition And Subtraction Formulas Ppt Download
slideplayer.com

Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
www.teachoo.com

1 Trigonometry Further Mathematics Zimbabwe Zimsec Cambridge
www.slideshare.net

Interconversion Between Inverse Trigonometric Ratios What Is Interconversion Between Inverse Trigonometric Ratios Examples Solutions Cuemath
www.cuemath.com

Tangent Half Angle Formula Wikipedia
en.wikipedia.org

Maclaurin Series Of Sin X Video Khan Academy
www.khanacademy.org

Euler S Formula Wikipedia
en.wikipedia.org

Simplify Trig Expression Cos X 4 Sin X 4 Youtube
www.youtube.com

Summary Of Trigonometric Identities
www2.clarku.edu

Relating Trigonometric Functions Trigonometry Socratic
socratic.org

Euler S Formula Wikipedia
en.wikipedia.org

Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
www.math10.com

Section 7 3 Double Angle Half Angle And Sum
studylib.net

Solved Section 7 3 Double Angle Half Angle And Product Chegg Com
www.chegg.com

Using Identities
colalg.math.csusb.edu

38 Solved Questions Of Trigonometry For Trigonometric Identities Trigonometric Identities Trigonometry Sci Pi
scipitutor.blogspot.com

Maclaurin Expansion Of Sin X The Infinite Series Module
blogs.ubc.ca

Solved Give The Formula For Cos 2x In Terms Of Cos X And Chegg Com
www.chegg.com

Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id 3998440
www.slideserve.com

Solved 5 Using Euler S Formula E Cos X J Sin X A Chegg Com
www.chegg.com

Trigonometric Functions Introduction Sine Cosine Videos And Examples
www.toppr.com

5 5 Multiple Angle And Product Sum Formulas Find All Solutions In Ppt Download
slideplayer.com

Summary Of Trigonometric Identities
www2.clarku.edu

Example 3 Show I Sin 1 2x Root 1 X2 2 Sin 1 X Examples
www.teachoo.com

Applications Of Euler S Formula Complex Multiplication Exponentiation By Ozaner Hansha Medium
medium.com

14 2 Trigonometric Identities
mathonweb.com

Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcrufcxhq Ratnfmnwjl0omanubci Zyowpgwc Wxltluhyeoz9j Usqp Cau
encrypted-tbn0.gstatic.com

Writing Trig Functions In Terms Of Sine And Cosine Youtube
www.youtube.com

Sine And Cosine Addition Formulas Solutions Examples Videos
www.onlinemathlearning.com

Trigonometric Identities Topics In Trigonometry
themathpage.com

Math34 Trigonometric Formulas
www.slideshare.net

Double Angle Identities Trigonometry Socratic
socratic.org

www.nagwa.com

The Maclaurin Expansion Of Cos X The Infinite Series Module
blogs.ubc.ca

Ex 2 2 8 Chapter 2 Class 12 Inverse Tan 1 Cos X Sin X
www.teachoo.com

Trigonometric Identities Ppt Download
slideplayer.com

Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Download
slideplayer.com