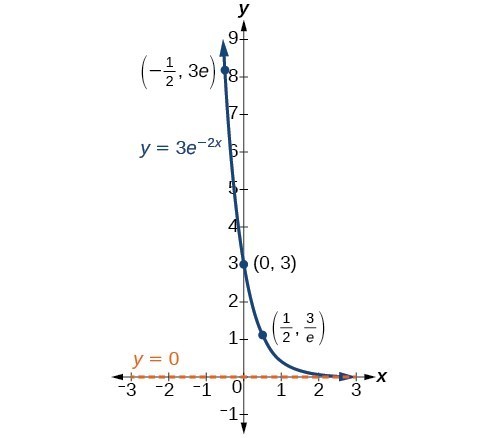
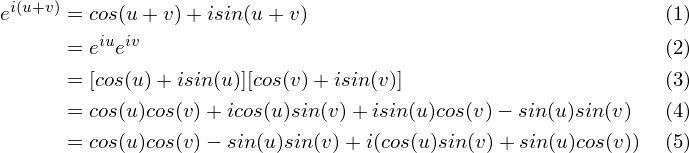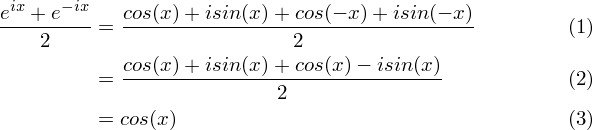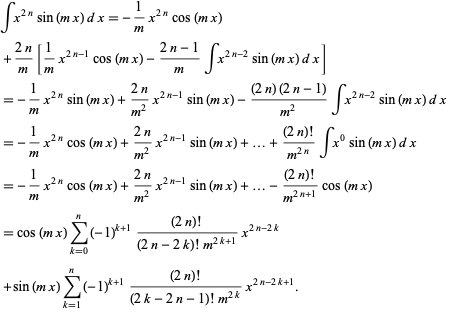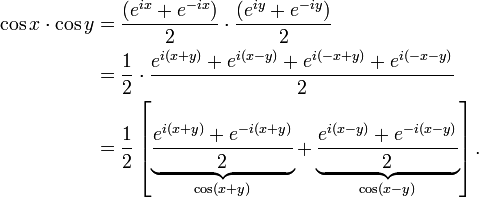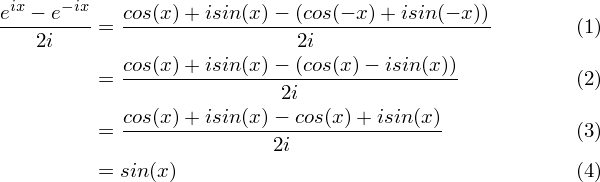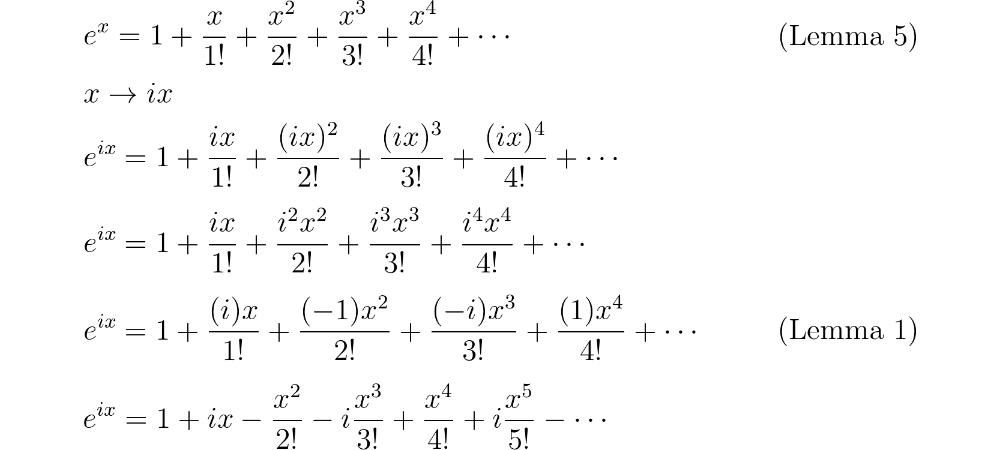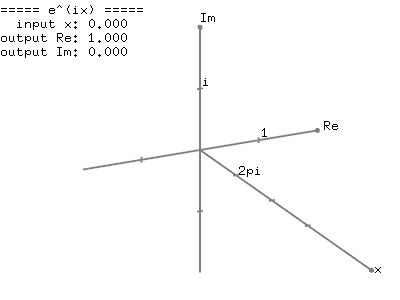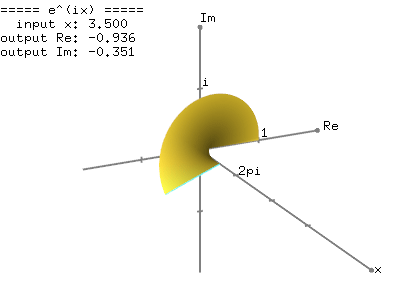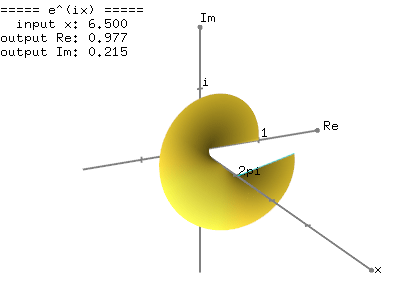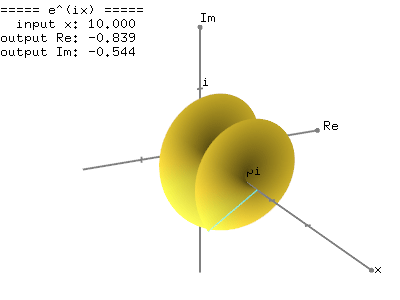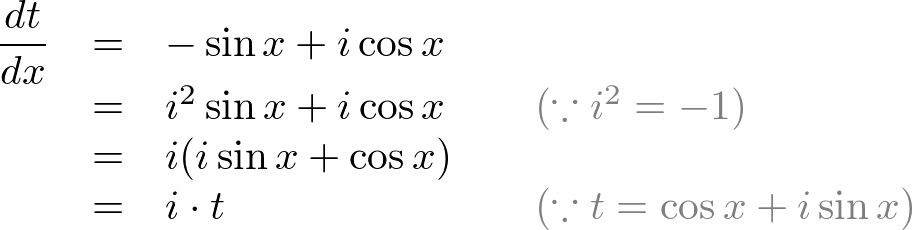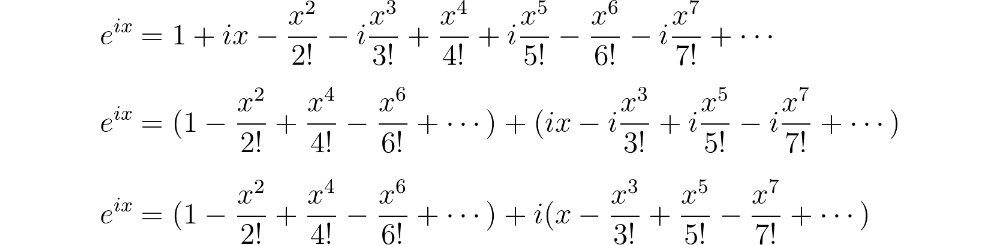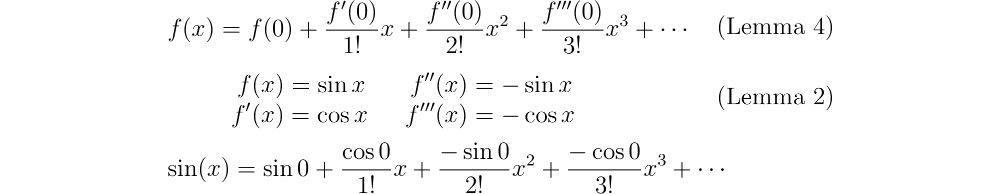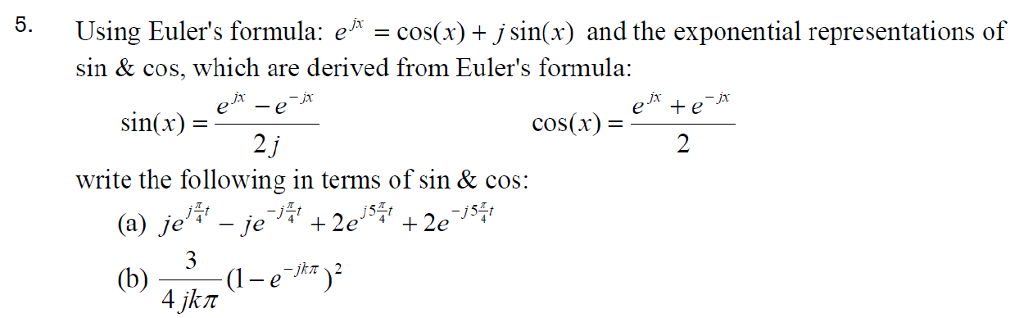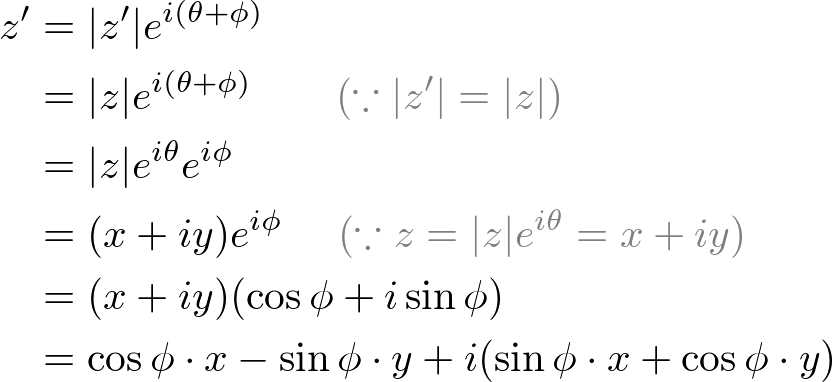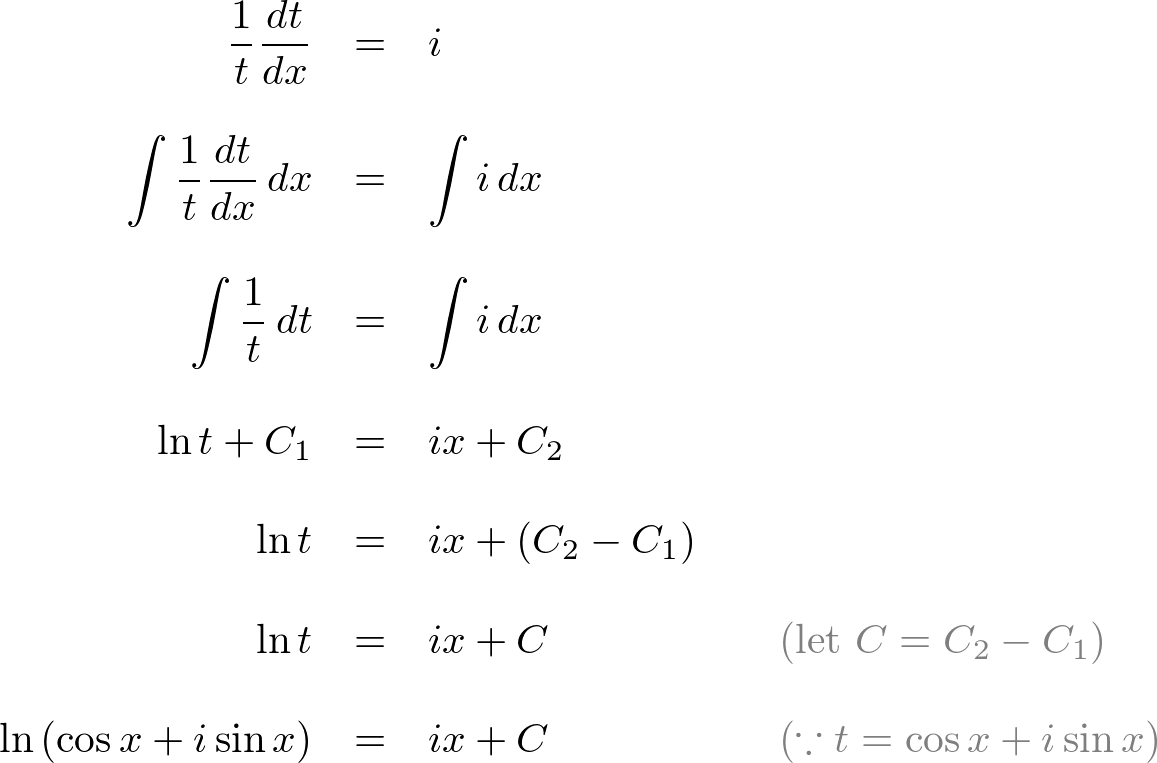Cos X Formula In Terms Of Exponential
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcruigcca6dwghwqzajusvxi0f7ckb9srlhnoqviex3jh1l0 Bug Usqp Cau
encrypted-tbn0.gstatic.com
Euler S Formula
www.ctralie.com
Complex Numbers 4 4 Cos And Sine To Complex Exponential Youtube
www.youtube.com
Integration Formulas
www.slideshare.net
2
Introduction To Complex Fourier Series Pdf Free Download
docplayer.net
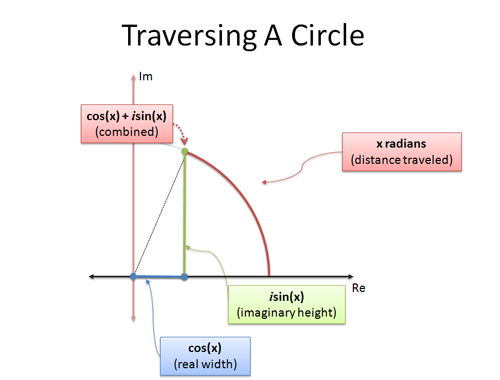
Putting all the results together the complex exponential function is found to be fz ez excosy iexsiny by setting x 0 we then deduce the euler formula.
Cos x formula in terms of exponential. Eiy cosy isiny. In complex analysis the hyperbolic functions arise as the imaginary parts of sine and cosinethe hyperbolic sine and the hyperbolic cosine are. Trigonometry and complex exponentials amazingly trig functions can also be expressed back in terms of the complex exponential.
If you define the functions sin and cos as mathcos x dfraceixe ix2tag1math mathsin x dfraceix e ix2itag2math. The complex logarithm using polar coordinates and eulers formula allows us to dene the complex exponential as exiy exeiy11 which can be reversed for any non zero complex number written in polar form as eiby inspectionx ln. Relations between cosine sine and exponential functions 45 46 47 from these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that were immensely painful to prove back in high school.
It means a is multiplied by itself x times. Displaystyle e ixcos xisin x. It can be veried that ez1z2 ez1ez2 another basic property of the exponential function.
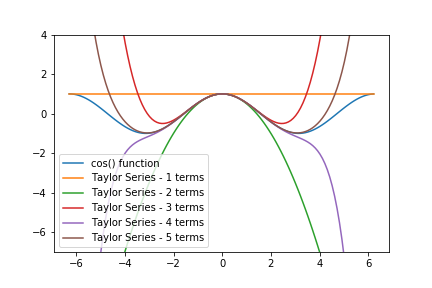
X is the exponent in the exponential expression a x. A polynomial with an innite number of terms given by expx 1 x x2 2. This is very surprising.
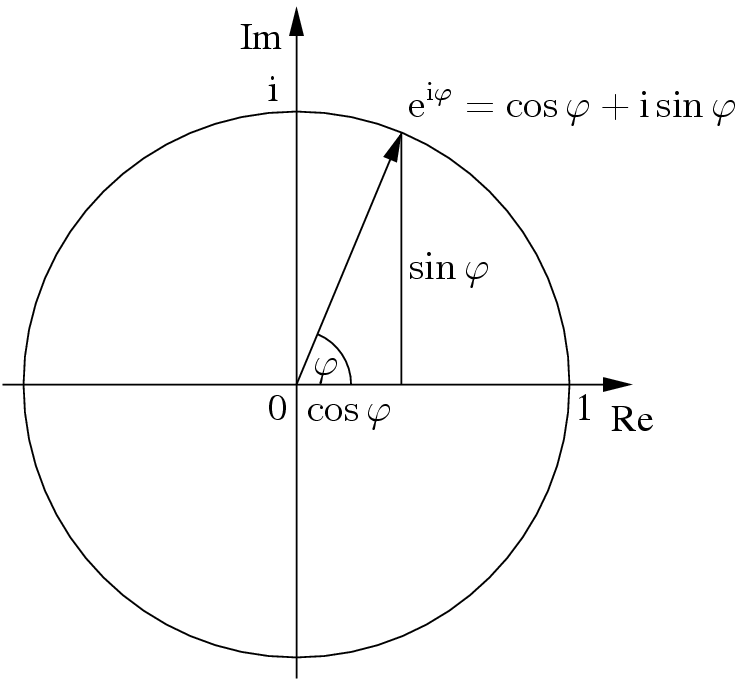
By the end of this course we will see that the exponential function can be represented as a power series ie. There are similar power series expansions for the sine and cosine given by cos 1 2. Eulers formula named after leonhard euler is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function.
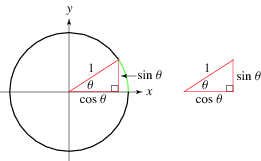
The hyperbolic functions take a real argument called a hyperbolic anglethe size of a hyperbolic angle is twice the area of its hyperbolic sectorthe hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector. Yto which we can also add any integer multiplying 2toyfor another solution. Logarithm an expression of the form log a x.
Eulers formula states that for any real number x.
List Of Integrals Of Trigonometric Functions Wikipedia
en.wikipedia.org
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqt73ivvpbnhpfppm1foxkhgl16ztkrrawseqjsf5gmxaxiykcs Usqp Cau
encrypted-tbn0.gstatic.com
Derivatives Of Hyperbolic Functions
www.math24.net
Limits Formula Sheet Chapter 13 Class 11 Maths Formulas Teachoo
www.teachoo.com
Why Is Math E I Theta Cos Theta I Sin Theta Math Quora
www.quora.com
Introduction To Complex Fourier Series Pdf Free Download
docplayer.net
2
Solved Suppose That A Waveform X T Is Represented As A S Chegg Com
www.chegg.com
Chapter 3 Elementary Functions
studylib.net
2
Euler S Formula
www.ctralie.com
Solved Hi I Am Quite Stumped With Some Questions From A Chegg Com
www.chegg.com
Integration Using Euler S Formula Wikipedia
en.wikipedia.org
Limits Formula Sheet Chapter 13 Class 11 Maths Formulas Teachoo
www.teachoo.com
Sine Integral From Wolfram Mathworld
mathworld.wolfram.com
2
Why Is Math E I Theta Cos Theta I Sin Theta Math Quora
www.quora.com
6 Derivative Of The Exponential Function
www.intmath.com
Solved How Many Non Zero Complex Exponential Fourier Seri Chegg Com
www.chegg.com
Hyperbolic Functions Wikipedia
en.wikipedia.org
How To Integrate Exponential And Trigonometric Functions E X Cosx Sneaky Trick Youtube
www.youtube.com
Solved Given A Cosine Wave Of Frequency 1 Pi Hz And A Chegg Com
www.chegg.com
Solved 2 Euler S Formula Relates The Complex Exponential Chegg Com
www.chegg.com
Solved D Z Cos X Hint Use Euler S Formula To Expr Chegg Com
www.chegg.com
How To Find The Period Of Cosine Functions Video Lesson Transcript Study Com
study.com
Sum Of Sinusoids Using Complex Exponential Signals
www.music.mcgill.ca
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqt73ivvpbnhpfppm1foxkhgl16ztkrrawseqjsf5gmxaxiykcs Usqp Cau
encrypted-tbn0.gstatic.com
Euler S Formula Wikipedia
en.wikipedia.org
List Of Integrals Of Exponential Functions Wikipedia
en.wikipedia.org
Exponential Functions Vs Trigonometric And Hyperbolic Functions
www.efunda.com
Exponential Fourier Series Example 3 Youtube
www.youtube.com
Solved Suppose A Periodic Signal X T Is Represented By I Chegg Com
www.chegg.com
Krista King Math Online Math Tutor Integration By Parts Everything You Need To Know Downloads
www.kristakingmath.com
Solved Suppose A Periodic Signal X T Is Represented By I Chegg Com
www.chegg.com
Solution Manual Chapter 07 Exponential Logarithmic And Inverse T
www.slideshare.net
2
Taylor Series Expansions Of Exponential Functions
www.efunda.com
Cos 4x In Terms Of Cos X Youtube
www.youtube.com
Intuitive Understanding Of Euler S Formula Betterexplained
betterexplained.com
Some Exponential Integrals
galileo.phys.virginia.edu
Cosine From Wolfram Mathworld
mathworld.wolfram.com
Why Is Math E I Theta Cos Theta I Sin Theta Math Quora
www.quora.com
How To Calculate Integrals Of Exponential Functions Video Lesson Transcript Study Com
study.com
Integration By Parts With Exponential And Trig Youtube
www.youtube.com
Derivatives Of Logarithmic And Exponential Functions Is An Important Topic Of Calculus Mathematics We Generally Denote The Lo Calculus Exponential Mathematics
www.pinterest.com
Ex 7 6 18 Integrate E X 1 Sin X 1 Cos X Teachoo
www.teachoo.com
Sinusoids And Complex Numbers Advances Signals And Systems
sites.google.com
Solved Problem 3 10 Points With The Help Of The Euler Chegg Com
www.chegg.com
Circuit Network Analysis Chapter3 Fourier Analysis
www.slideshare.net
List Of Integrals Of Exponential Functions Wikipedia
en.wikipedia.org
Solved Use Euler S Formula For The Complex Exponential To Chegg Com
www.chegg.com
Pdf Effcient Formulas For The Exact Integration Of Products Of Polynomials Exponentials And Trigonometric Functions
www.researchgate.net
Exponential Functions Vs Trigonometric And Hyperbolic Functions
www.efunda.com
Exponential Growth And Decay College Algebra
courses.lumenlearning.com
Integration Using Euler S Formula Wikipedia
en.wikipedia.org
Complex Numbers Reading Feynman
readingfeynman.org
Ex 9 3 5 Form Differential Equation Y Ex A Cos X B Sin X
www.teachoo.com
Derivation Of Fourier Series
lpsa.swarthmore.edu
Euler S Formula
www.ctralie.com
Complex Exponential Magnitude Video Khan Academy
www.khanacademy.org
Understanding Euler S Formula Leonhard Euler Is Commonly Regarded By Ozaner Hansha Medium
medium.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gctococbz Zfdhqltkcrch 7pcjl6imkf87rrw Usqp Cau
Given The Complex Number Express In The Trigonometric Form Euler S Formula Relationship Between Trigonometric Functions And The Complex Exponential Function Euler S Equation Or Identity
www.nabla.hr
In Class We Constructed Fourier Series In Terms O Chegg Com
www.chegg.com
Particular Solution For Sin Using Complex Exponentials Youtube
www.youtube.com
Euler S Formula Wikipedia
en.wikipedia.org
Euler S Equation
www.songho.ca
www.nagwa.com
Solved 5 Euler S Equations Are Defined As Sin X Cos X Chegg Com
www.chegg.com
Euler S Formula Wikipedia
en.wikipedia.org
Ch 15 Complex Oscillations Pdf
www.yumpu.com
Solved Hi Please Show Step By Step As I Don T Understand Chegg Com
www.chegg.com
Complex Definitions Of Sine And Cosine Youtube
www.youtube.com
Euler S Formula Wikipedia
en.wikipedia.org
Understanding Euler S Formula Leonhard Euler Is Commonly Regarded By Ozaner Hansha Medium
medium.com
Video Finding The Power Of The Product Of Complex Numbers In Exponential Form Nagwa
www.nagwa.com
Euler S Formula Wikipedia
en.wikipedia.org
Complex Numbers Reading Feynman
readingfeynman.org
Euler S Formula Wikipedia
en.wikipedia.org
Using Complex Exponential To Show The Indefinite Integration Of Sin X Sinh X Dx Mathematics Stack Exchange
math.stackexchange.com
Fourier Transform Exponential Function From Wolfram Mathworld
mathworld.wolfram.com
Understanding Euler S Formula Leonhard Euler Is Commonly Regarded By Ozaner Hansha Medium
medium.com
The Complex Exponential Function Pdf Free Download
docplayer.net
Particular Integral Exponential Trigonometric Quadratic Functions By Bilal Mustafa Youtube
www.youtube.com
Solved 5 Using Euler S Formula E Cos X J Sin X A Chegg Com
www.chegg.com
The Maclaurin Expansion Of Cos X The Infinite Series Module
blogs.ubc.ca
Euler S Equation
www.songho.ca
Intro To Quantum 5 B Convert Cos And Sin To Complex Exponential Youtube
www.youtube.com
Euler S Equation
www.songho.ca
Euler S Equation
www.songho.ca
Euler S Formula On Complex Numbers Expii
www.expii.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcsz Gmn6uboybopyazro74q2pnwwm Wivi9nkmevf3abv2 Qgqf Usqp Cau
encrypted-tbn0.gstatic.com
Solved Suppose A Periodic Signal X T Is Represented By I Chegg Com
www.chegg.com
Euler S Equation
www.songho.ca
Qpsk Modulation And Generating Signals
www.testandmeasurementtips.com
Trigonometric Functions Wikipedia
en.wikipedia.org
Euler S Formula Wikipedia
en.wikipedia.org
Taylor Series In Python Python For Undergraduate Engineers
pythonforundergradengineers.com
