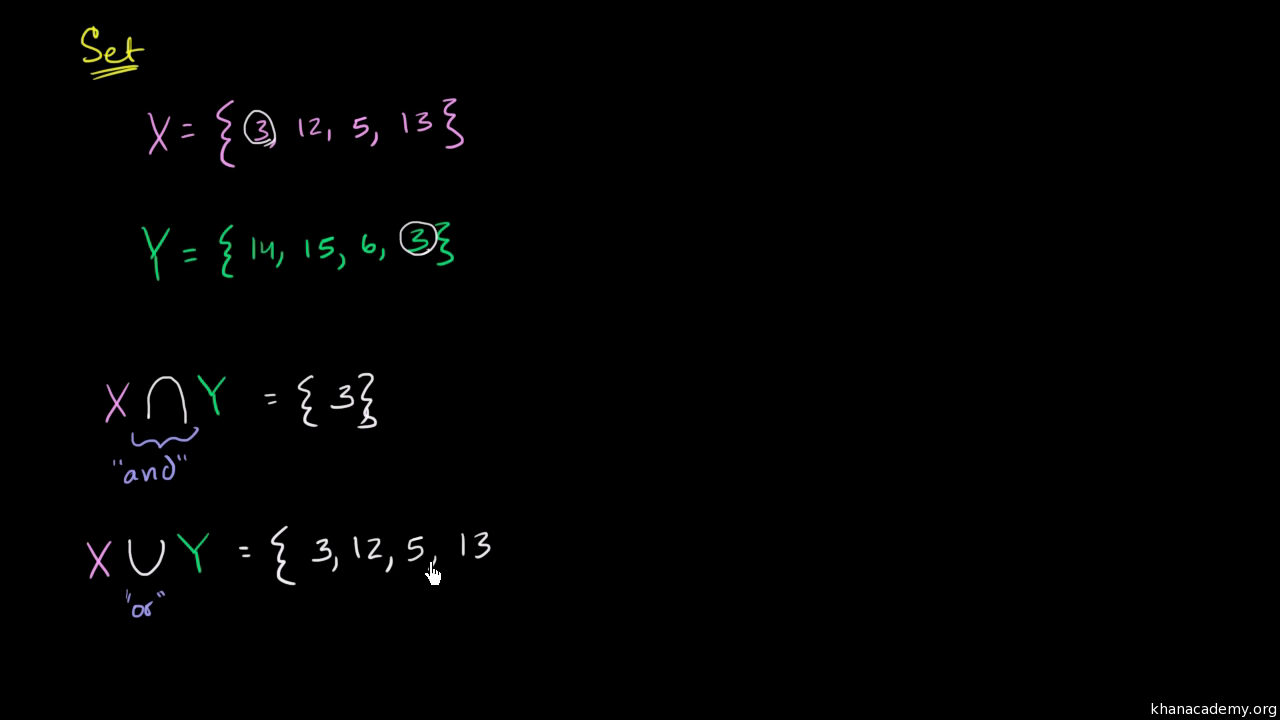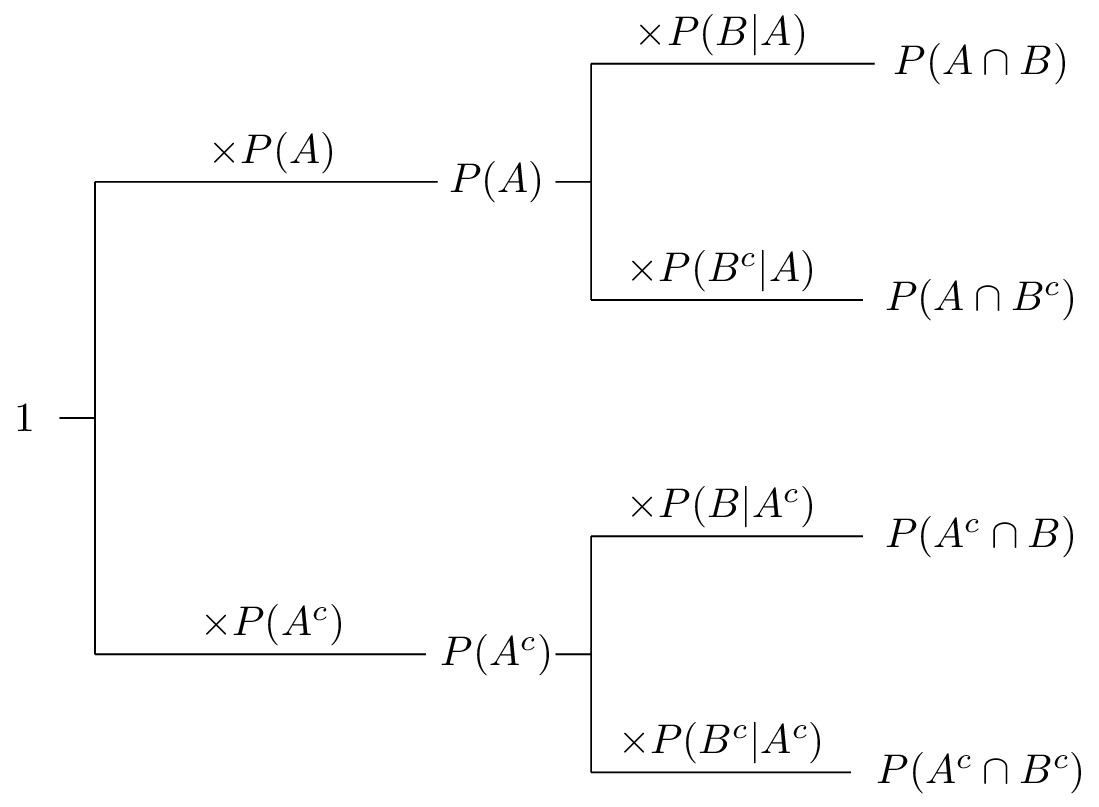A Intersection B Formula Example
Notice let me just rewrite it right over here.

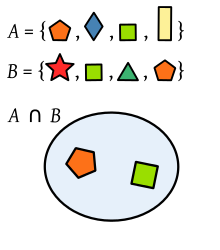
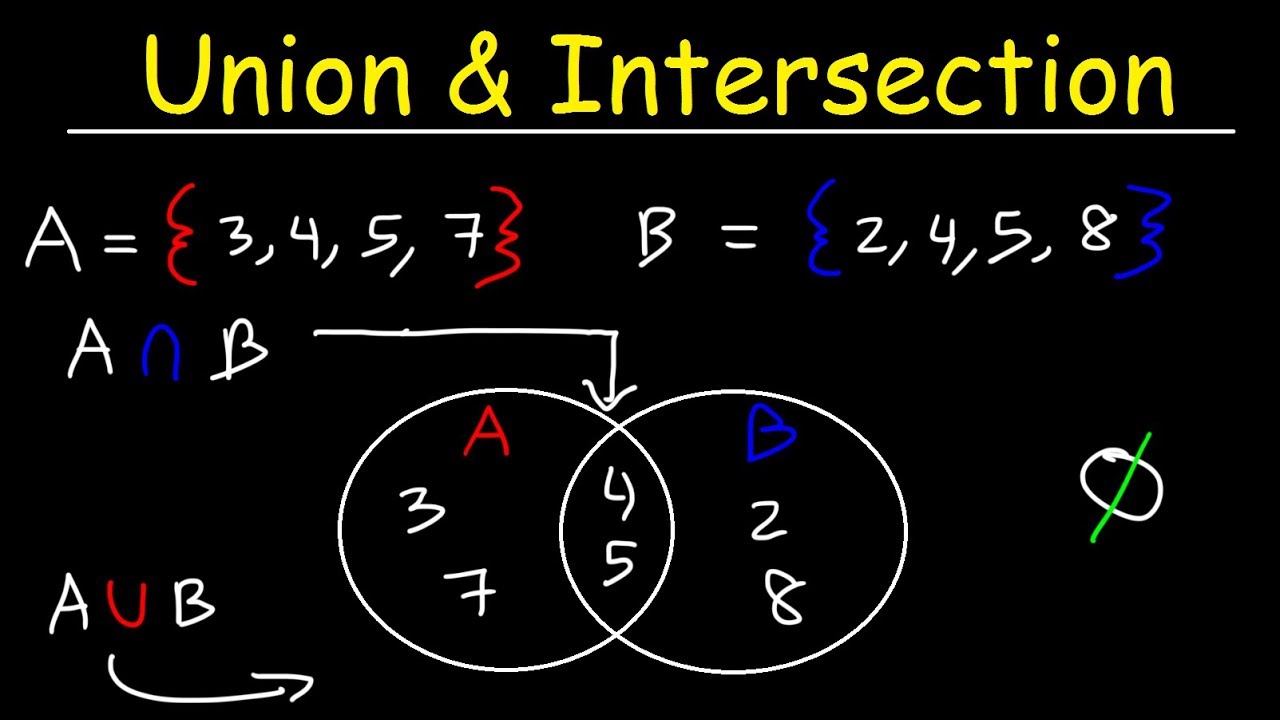
A intersection b formula example. A solved problem based on union and intersection of set theory. The intersection of events a and b. Let a 1 orange 1 pineapple 1 banana 1 apple and b 1 spoon 1 orange 1 knife 1 fork 1 apple a b 1 orange 1 apple example 2.
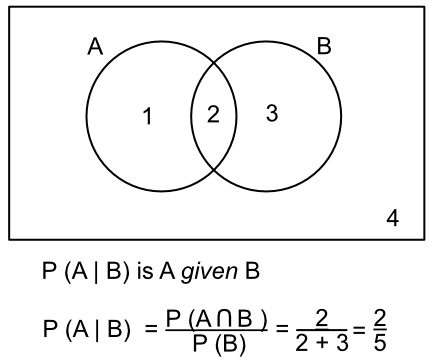
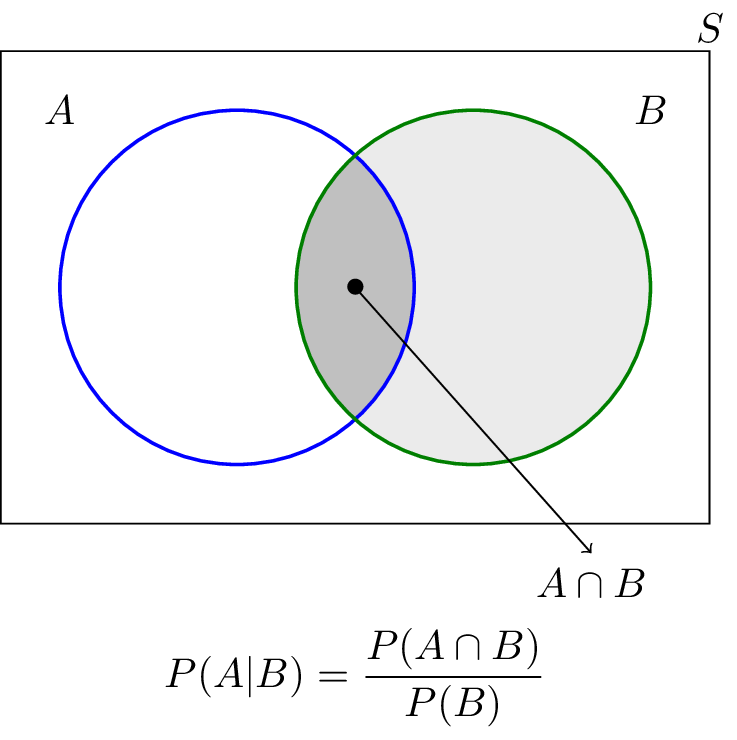
Lets think about a i want to do that in orange. The probability of b given a. The probability of the intersection of two events.
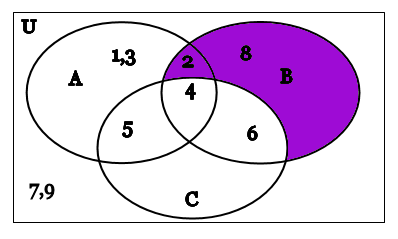
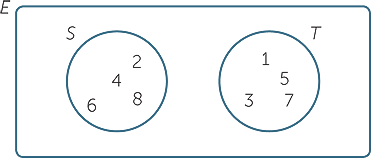
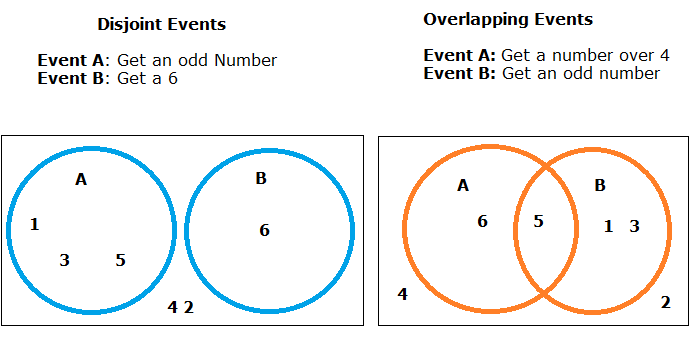
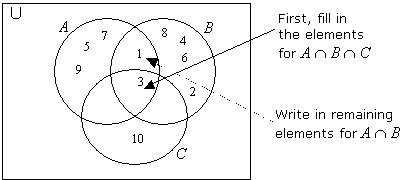
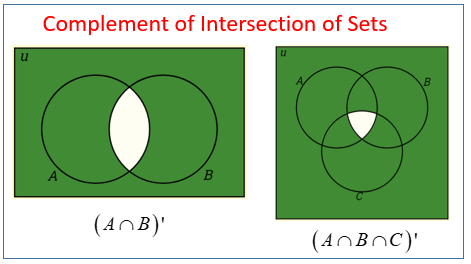
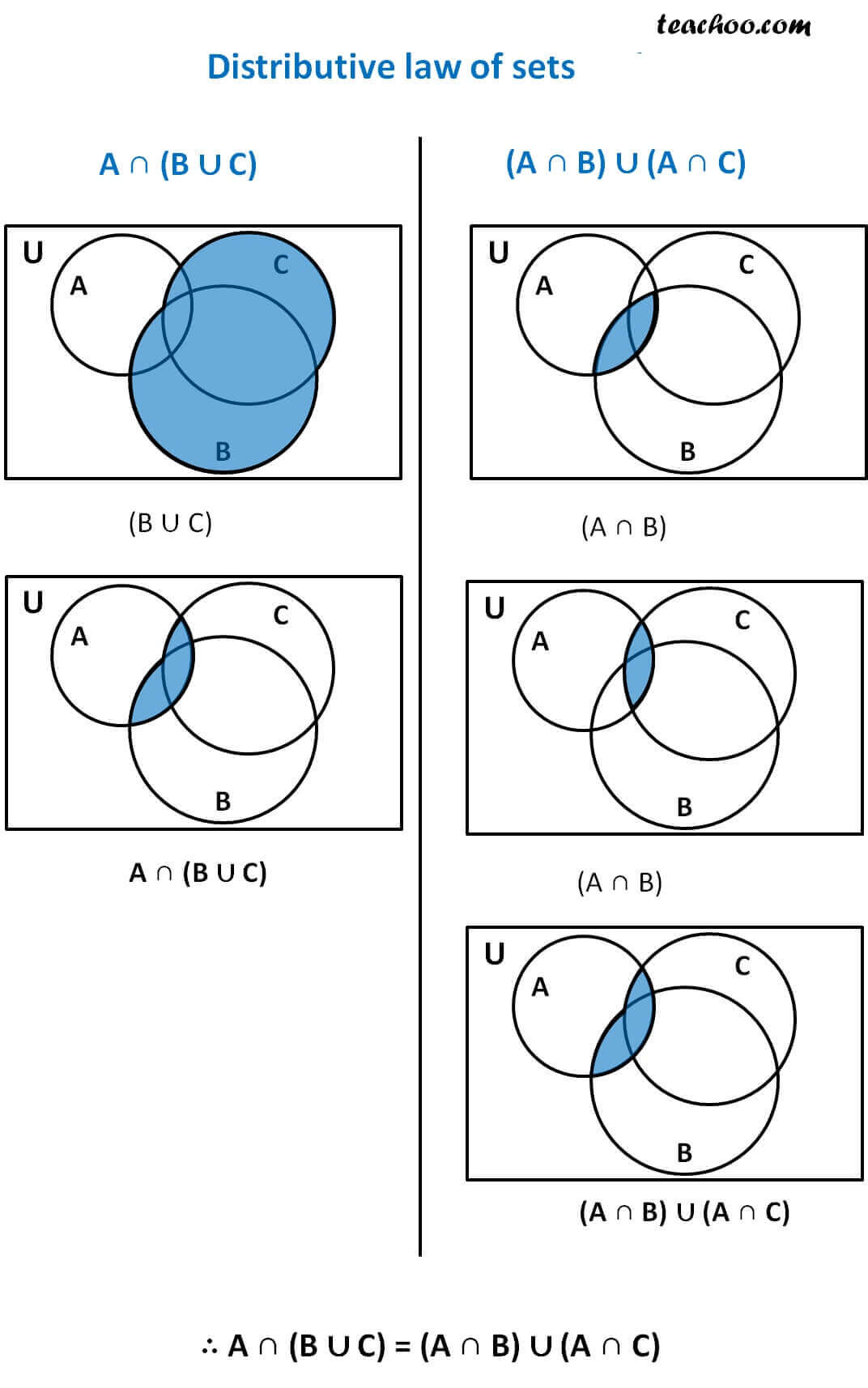
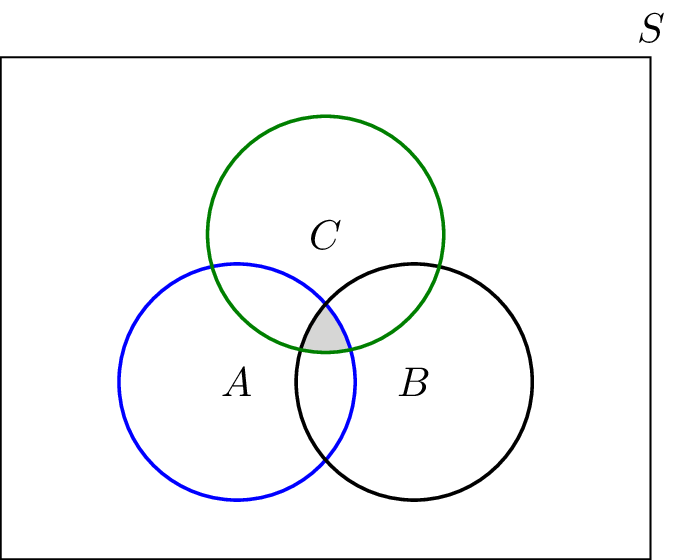
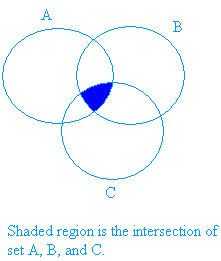
The intersection of the sets 1 2 3 and 2 3 4 is 2 3. Times that right over. Intersection of three sets in this lesson we will learn how to use venn diagrams to illustrate the intersection of two sets.
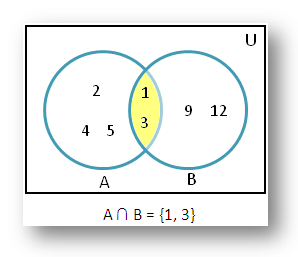
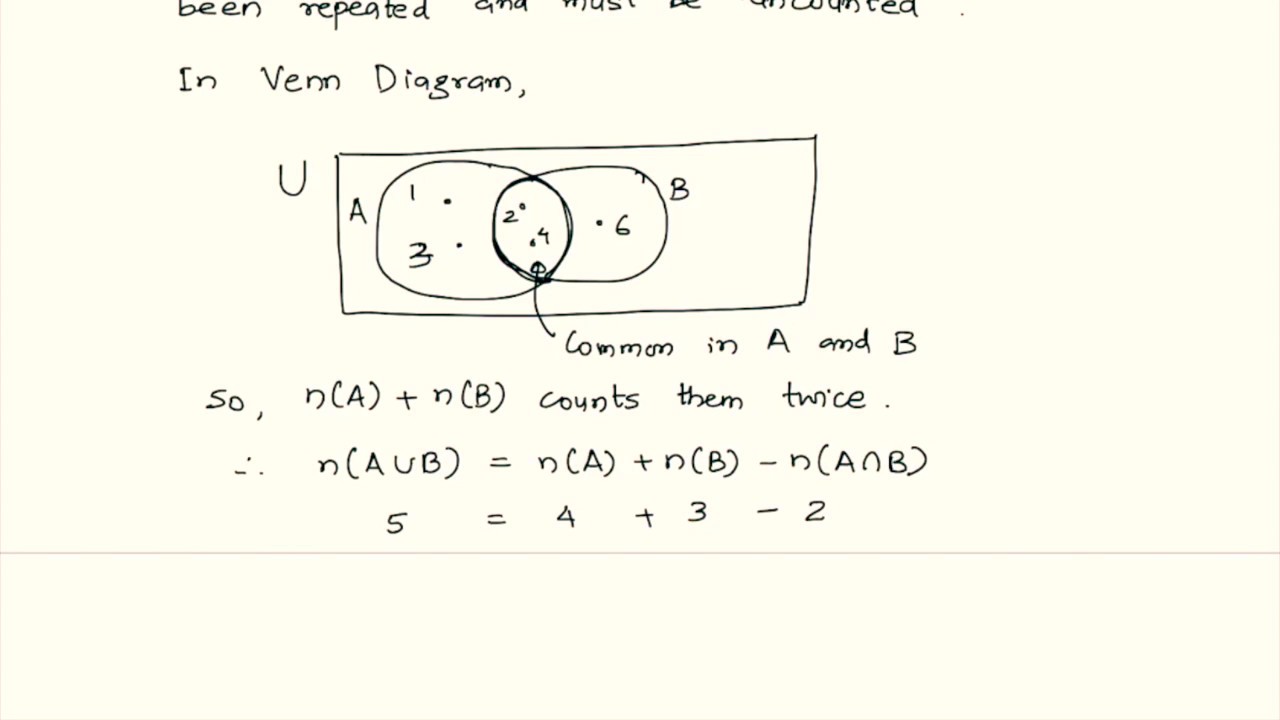
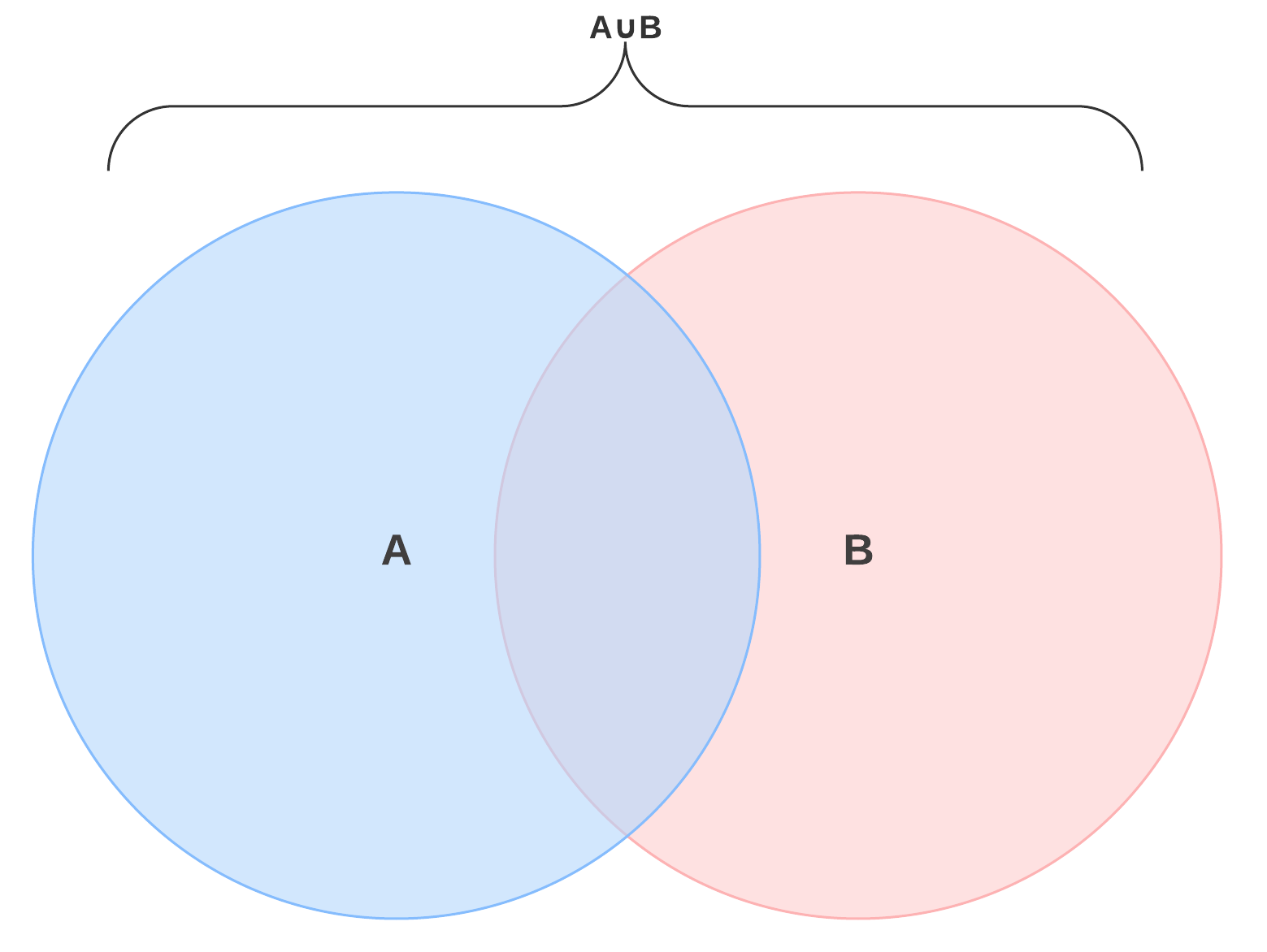
Learn to fill data in venn diagram. The probability of the union of events a and b is denoted by pa b. The set of 4 and 12 is the intersection of sets a and b.
The probability that events a or b occur is the probability of the union of a and b. The probability of the intersection of events a and b is denoted by pa b. 06 06 times the probability of b given a.
A 2 2 b 2 3 c 2 5. Find the intersection of a and b and then make a venn diagrams. Given straight line equations are.
Lets think about a union b. So just like that weve set up a situation an equation where we can solve for the probability of b given a. It is denoted by x y and is read x intersection y.
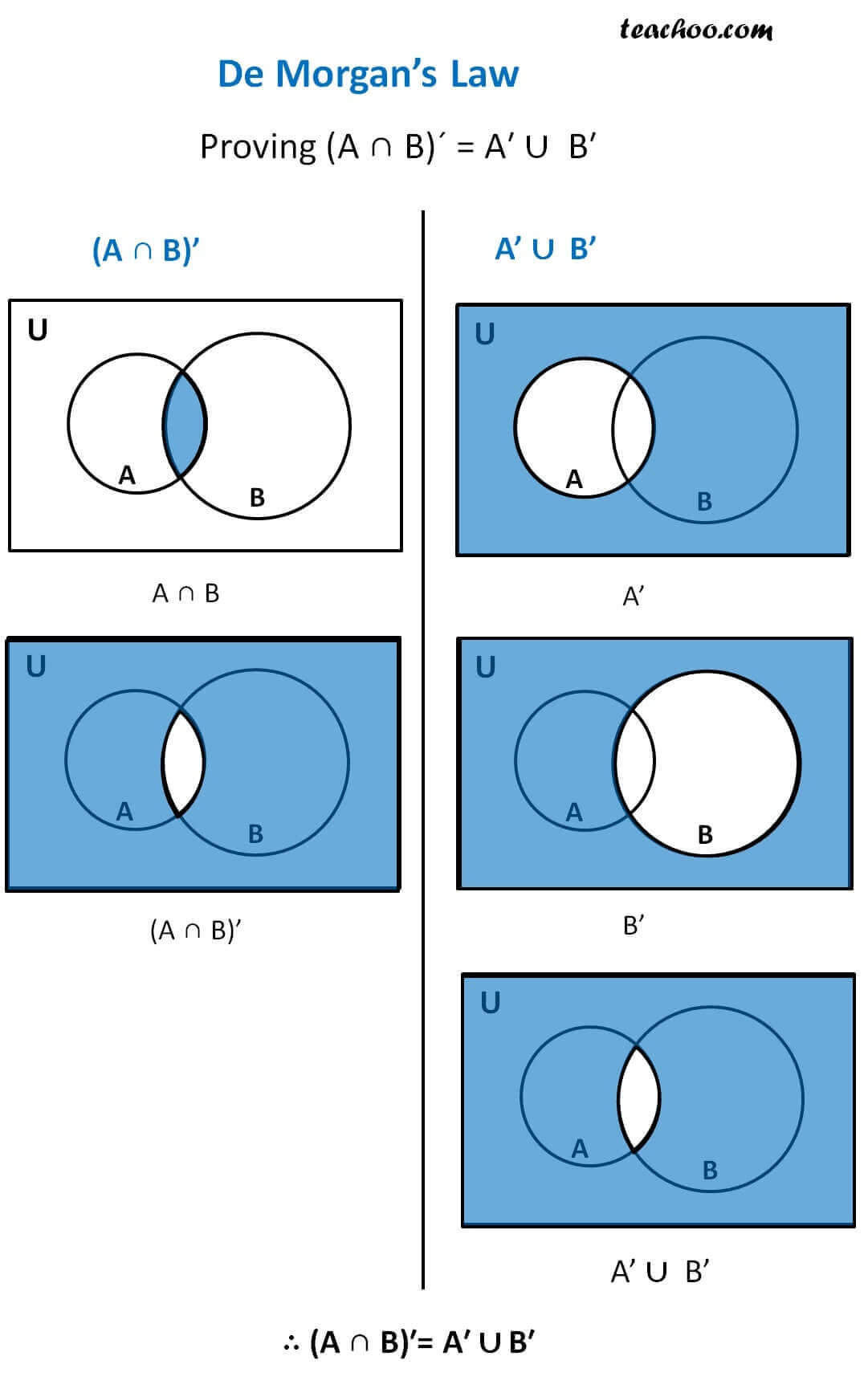
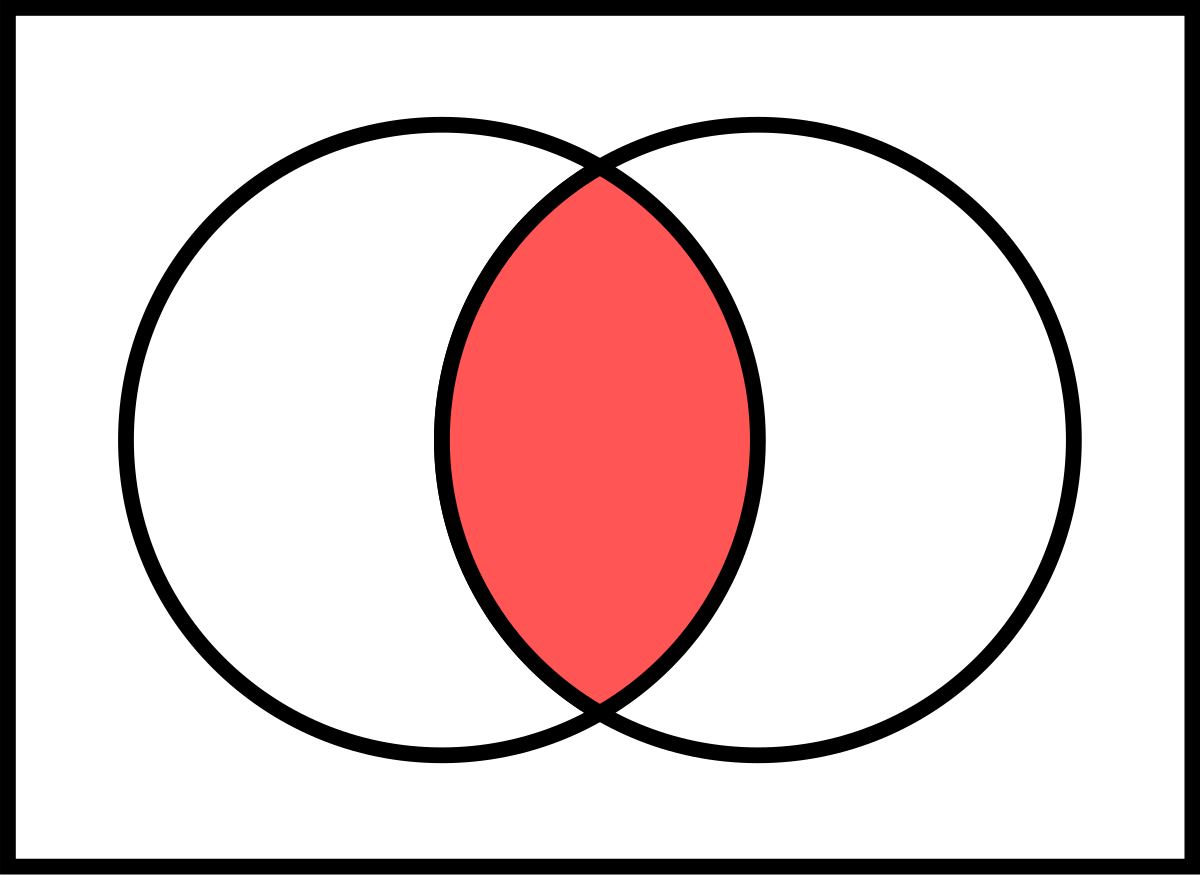
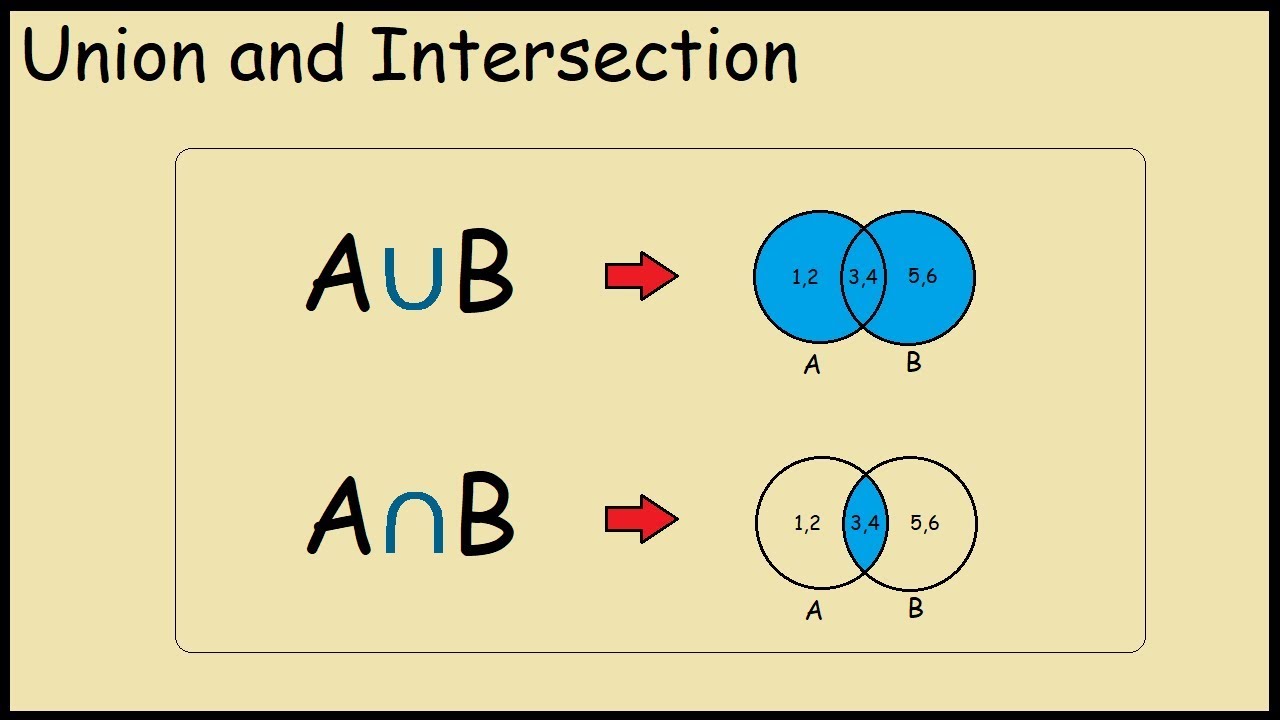
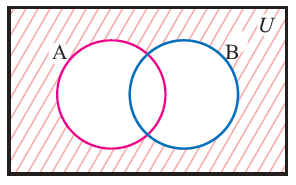
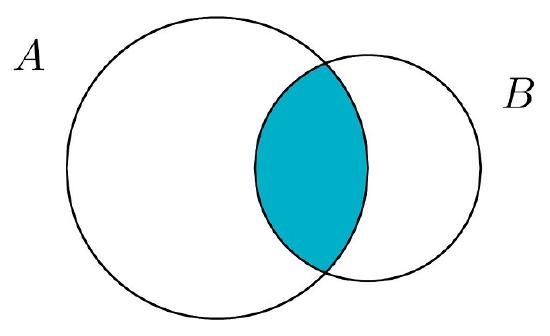
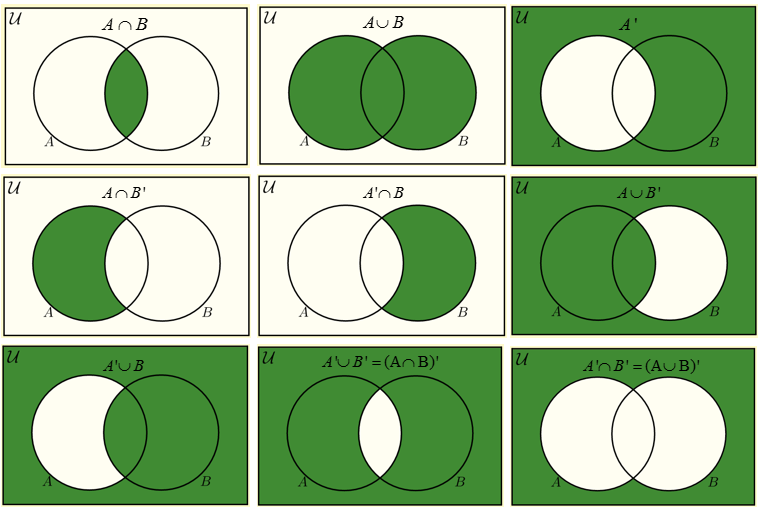
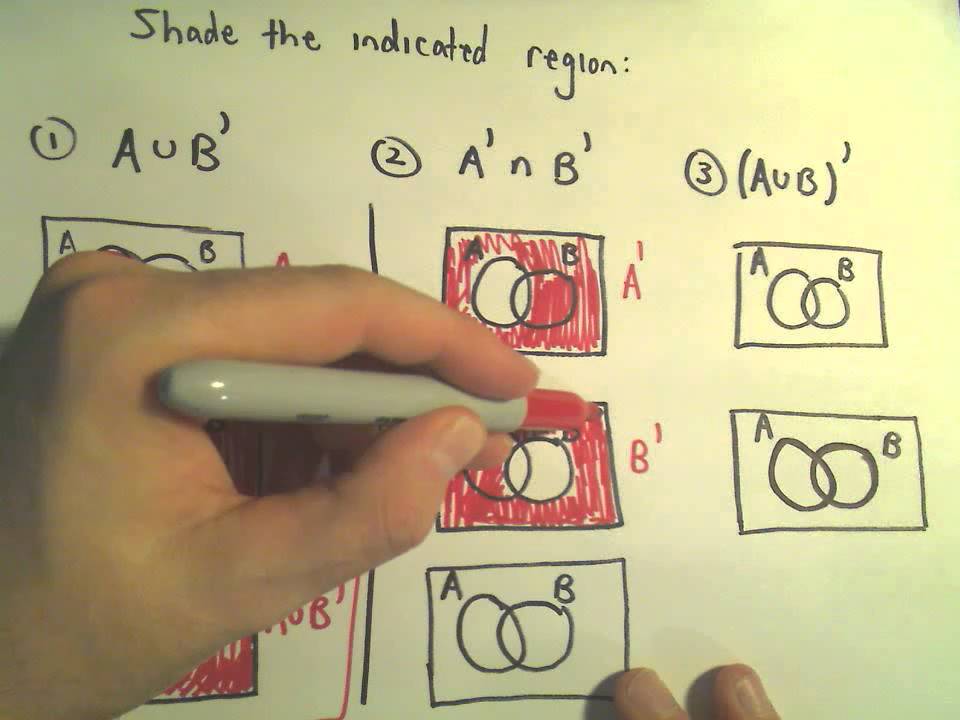
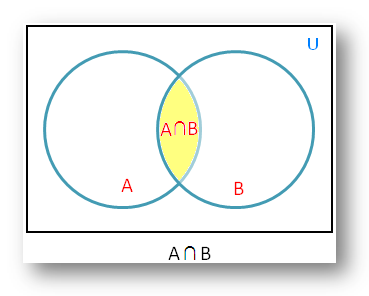
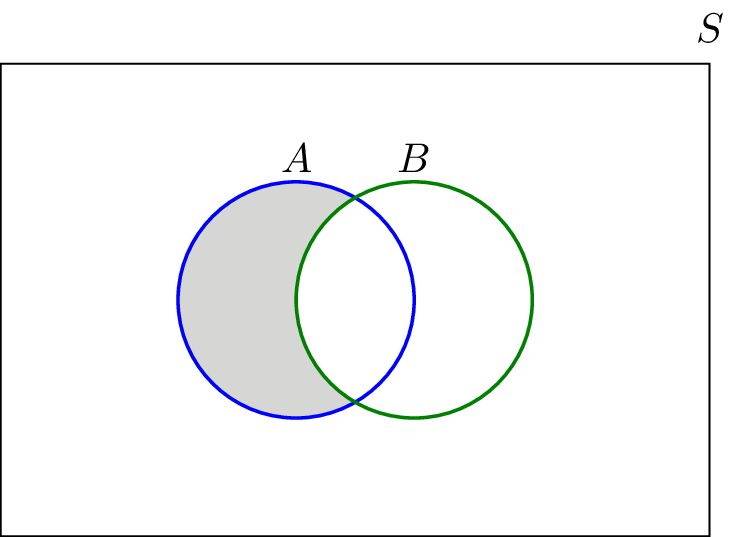
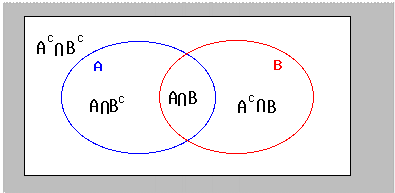
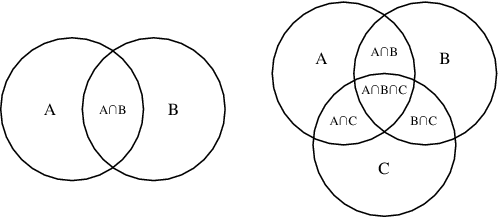
The intersection of two sets a and b denoted by a b is the set of all objects that are members of both the sets a and bin symbols. X 2y 1 0 and 2x 3y 5 0. The intersection of two sets x and y is the set of elements that are common to both set x and set y.
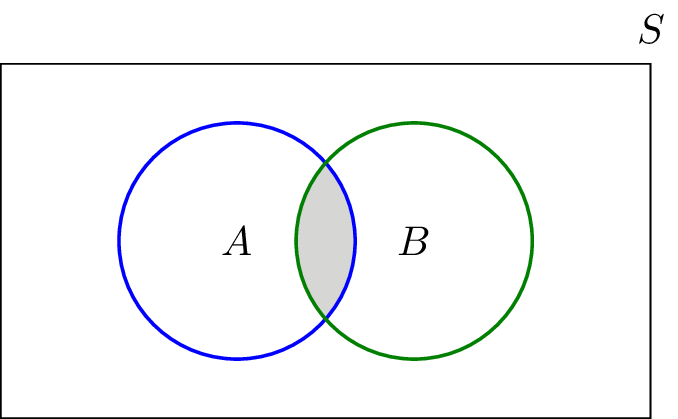
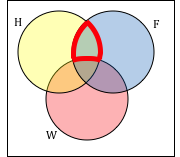
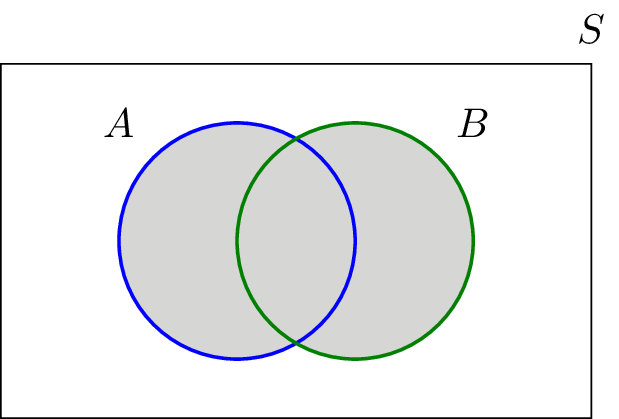
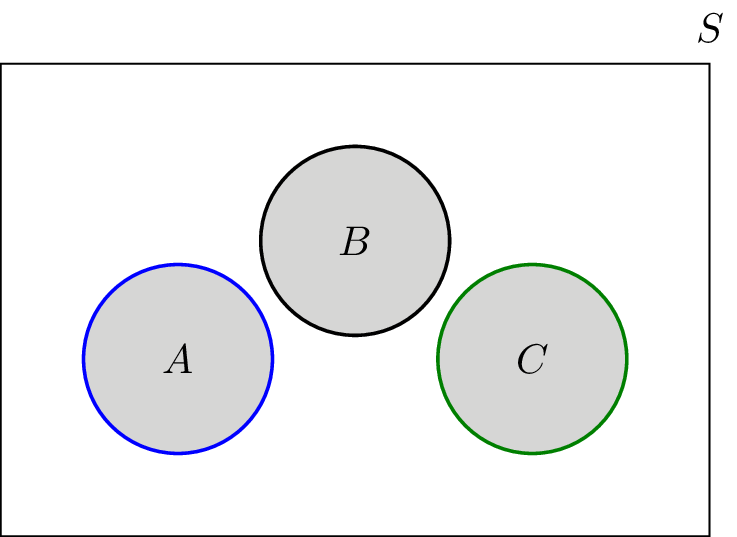
And we could even if we want to we could even label this as a new set. Actually ill write this part first. A visual representation of the intersection of events a and b in a sample space s is given in figure pageindex1.
That is x is an element of the intersection a b if and only if x is both an element of a and an element of b. Learn to find a union b using venn diagram. Here a 1 1 b 1 2 c 1 1.
Intersection point can be calculated using this formula. This version of the formula is most useful when we know the conditional probability of a given b as well as the probability of the event b. We could say set c is the intersection of a and b and its this set right over here.
We know that that is 06. Next we illustrate with examples. If this is the case then we can calculate the probability of the intersection of a given b by simply multiplying two other probabilities.
The intersection corresponds to the shaded lens shaped region that lies within both ovals. Find out the point of intersection of two lines x 2y 1 0 and 2x 3y 5 0. We know that this is 06.
To make it easy notice that what they have in common is in bold. Use of formula.



/conditional-56edf9de5f9b5867a1c1924c.jpg)

/conditional-56edf9de5f9b5867a1c1924c.jpg)










/conditional-56edf9de5f9b5867a1c1924c.jpg)




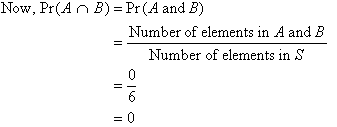




.gif)




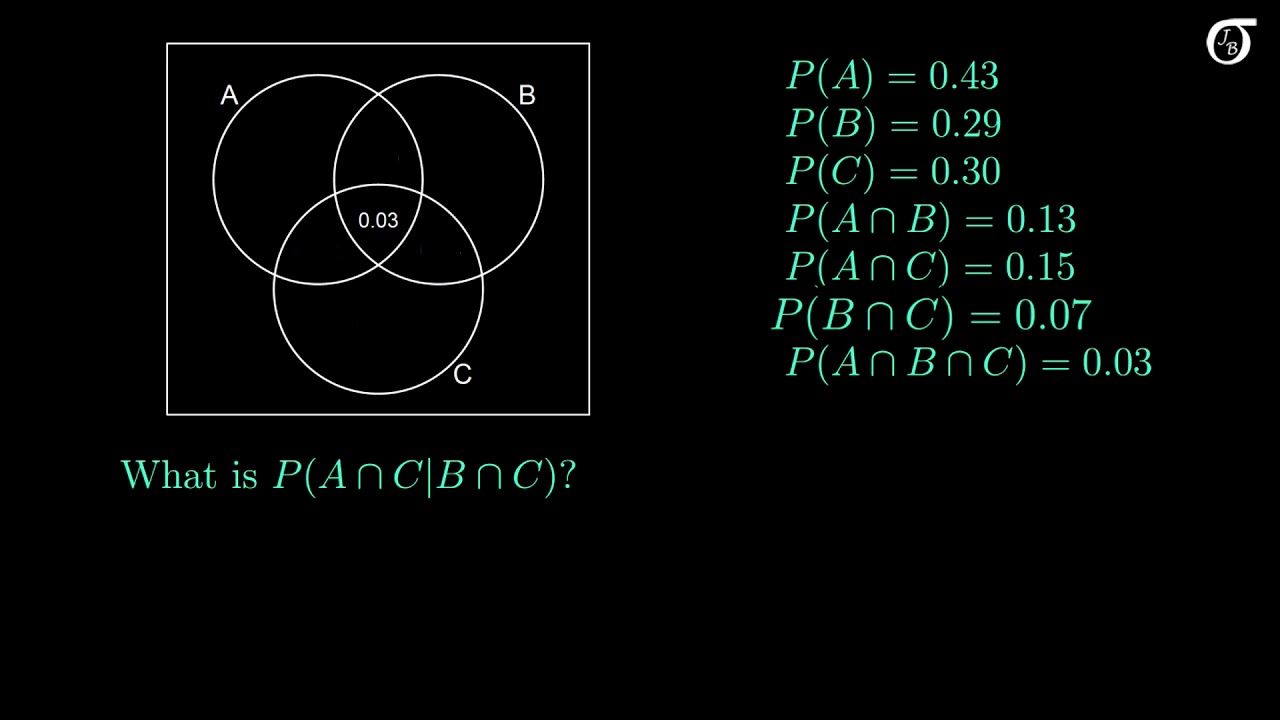


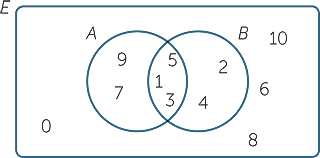
/addition-57bc15a75f9b58cdfdf894b7.jpg)







/intersection-57c632dd5f9b5855e5848ee8.jpg)


/complement-56a8fa9a5f9b58b7d0f6e9e7.jpg)

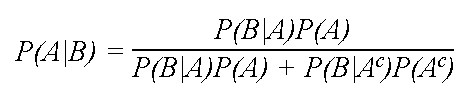

/JointProbabilityDefinition2-fb8b207be3164845b0d8706fe9c73b01.png)