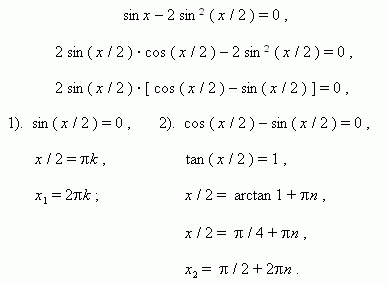2 Cos X Cos Y Formula
For sin x y we have sign on right right.
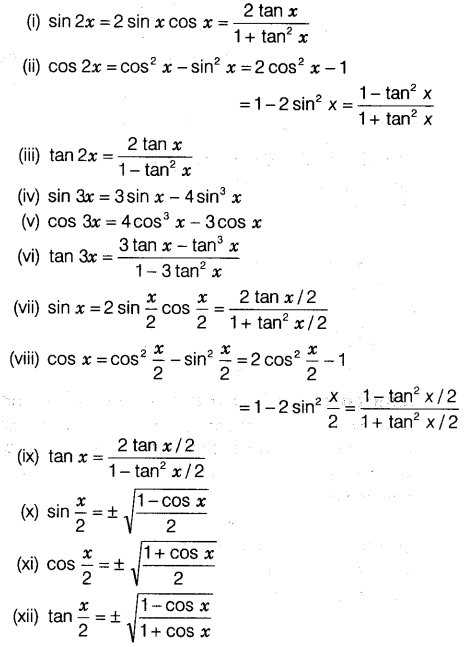
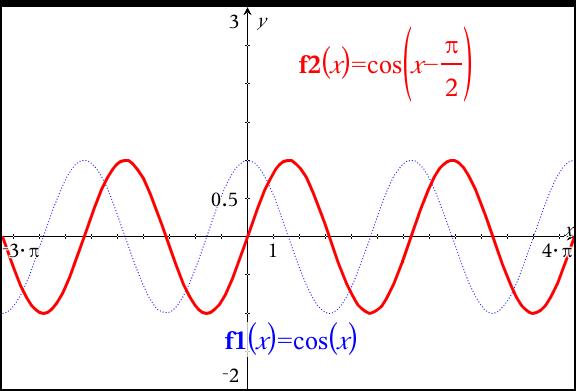
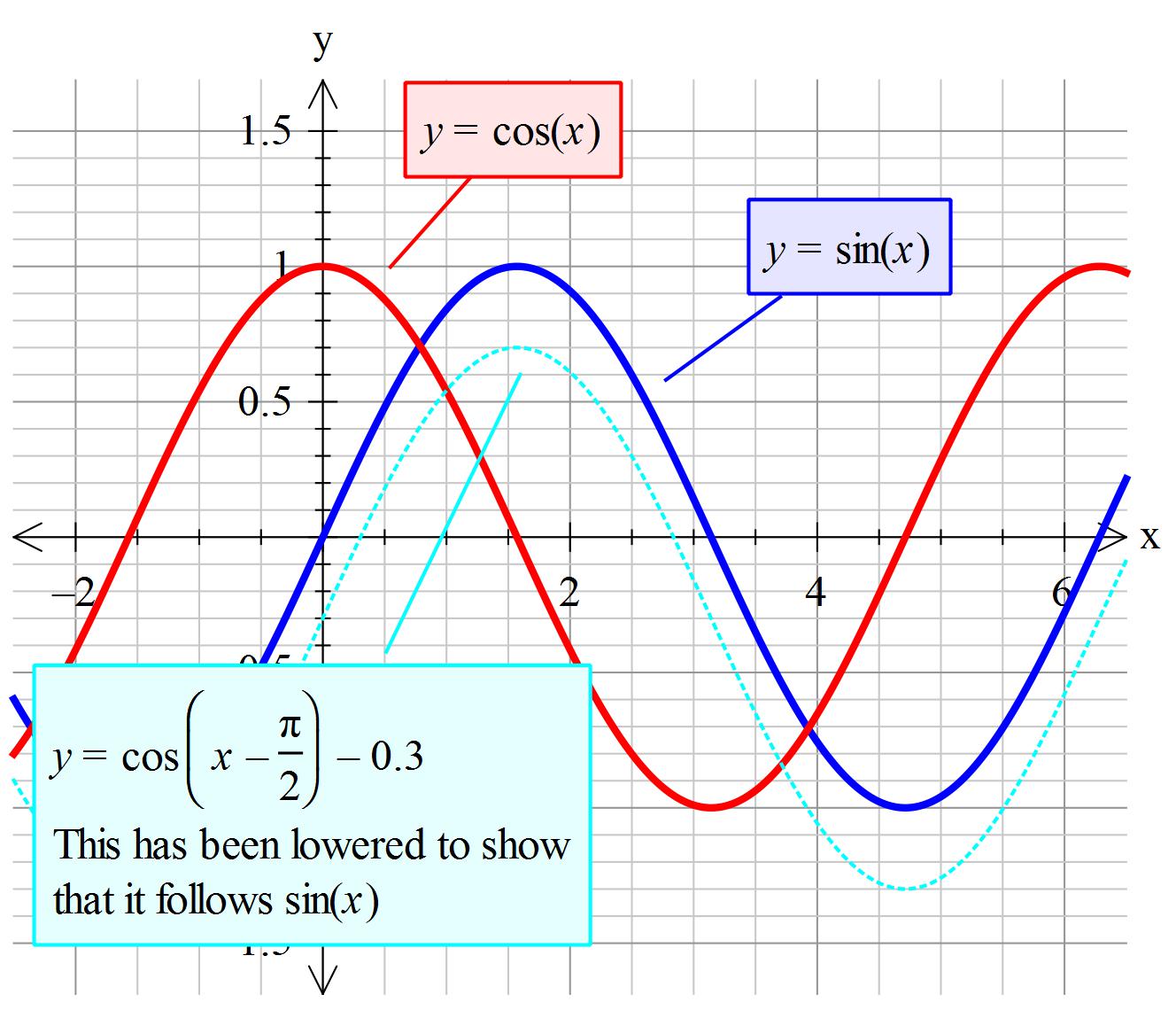
2 cos x cos y formula. Cosx y cosx y so you can apply your formula again. Look at the graphs of. Remember that cosine is a symmetrical function about x 0.
Sum to product formulas sinx siny 2sin xy 2 cos x y 2 sinx siny 2sin x y 2 cos xy 2 cosx cosy 2cos xy 2 cos x y 2 cosx cosy 2sin xy 2 sin x y 2 the law of sines sina a sinb b sinc c suppose you are given two sides aband the angle aopposite the side a. Below are some of the most important definitions identities and formulas in trigonometry. For cos it becomes opposite for cos x y we.
Lets see how we can learn it 1in sin we have sin cos. Solve the equation cos 2a sin a for p leq a p. Trigonometric identities and formulas.
This equation can be solved for either the sine or the cosine. Practice example for cos 2. It becomes 1 2 sin 2 a sin a.
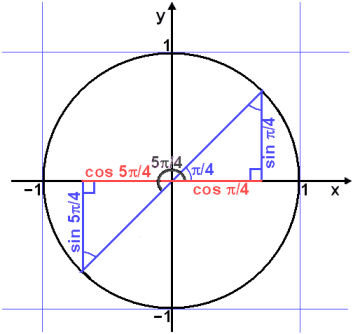
Where sin 2 o means sino 2 and cos 2 o means coso 2. For example sin x sin y is 2 sin xy2 cos x y2 cos x cos y is. In cos we have cos cos sin sin in tan we have sum above and product below 2for sin x y we have sign on right.
Sin y siny for all y. Cosx cos y sinx sin y now heres the trick. Sum to product identities are identities where we convert sin x sin y or cos x cos y into product of sin and cos.
X y 2 cos x y 2 difference to product formulas cosx cosy 2sin x. The height of the triangle is h bsina. Trigonometric functions identities formulas and the sine and cosine laws are presented.
This can be viewed as a version of the pythagorean theorem and follows from the equation x 2 y 2 1 for the unit circle. And this is how we get second double angle formula which is so called because you are doubling the angle as in 2a. 2 sin 2 a sin a 10.
Cot 2 x 1 csc 2 x. This means that cos y cosy for all y. Tan 2 x 1 sec 2 x.
Cosx y cos x cosy sin x sin y. Lets use the double angle formula cos 2a 1 2 sin 2 a. Sin 2 x cos 2 x 1.
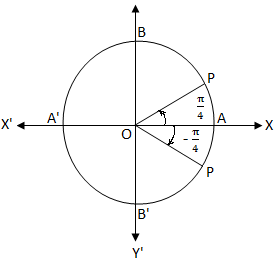
While right angled triangle definitions allows for the definition of the trigonometric functions for angles between 0 and radian 900 the unit circle definitions allow. The six trigonometric functions can be defined as coordinate values of points on the euclidean plane that are related to the unit circle which is the circle of radius one centered at the origin o of this coordinate system.
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqxgro Rps0zi3fesrjofsc35be8ntkcs 7oiz71san9lxzikuw Usqp Cau
encrypted-tbn0.gstatic.com

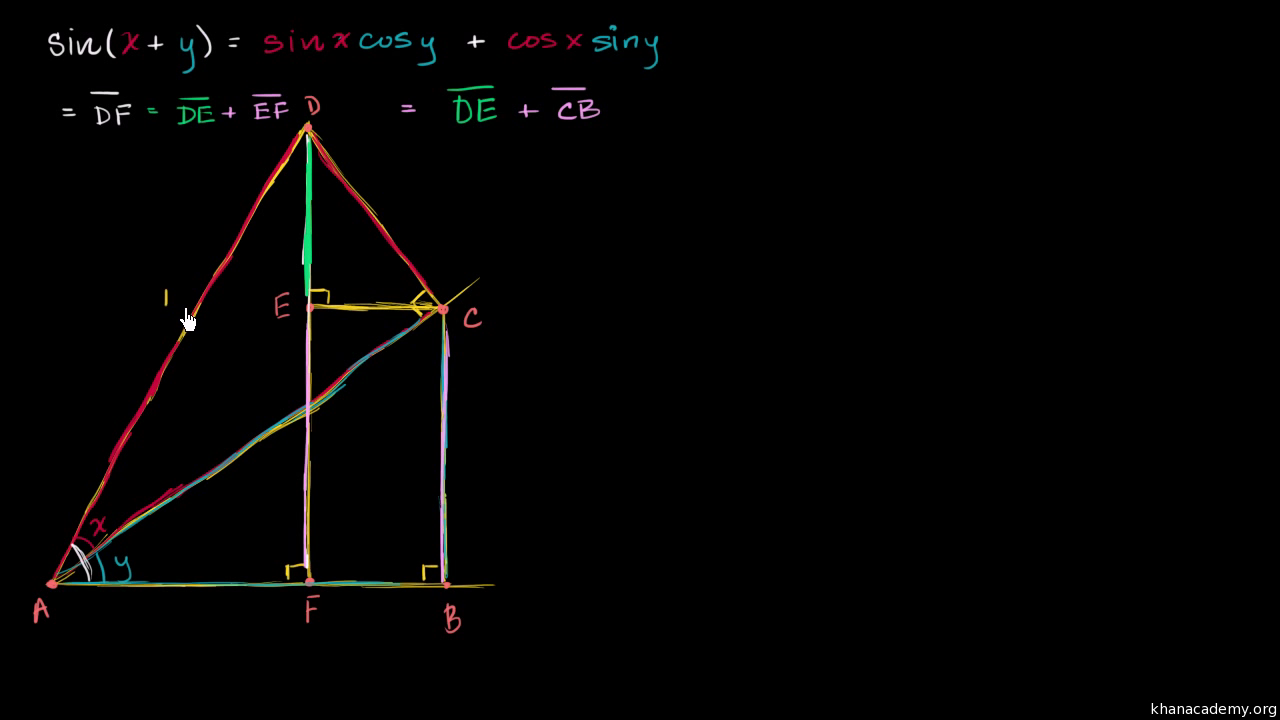




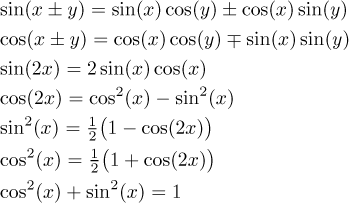










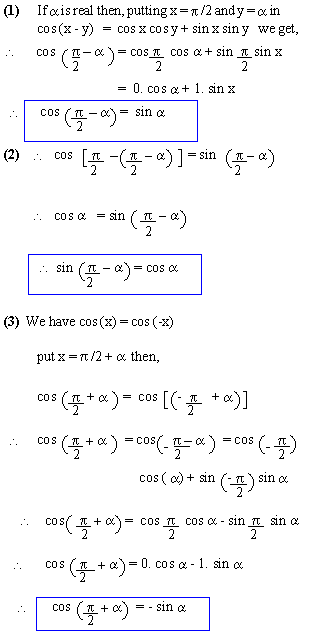




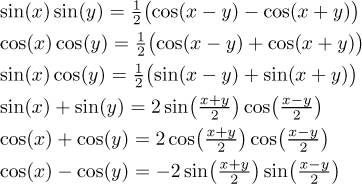












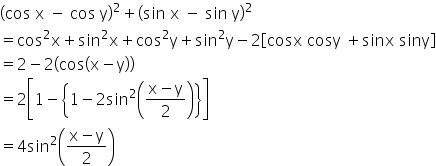









.jpg)






.gif)