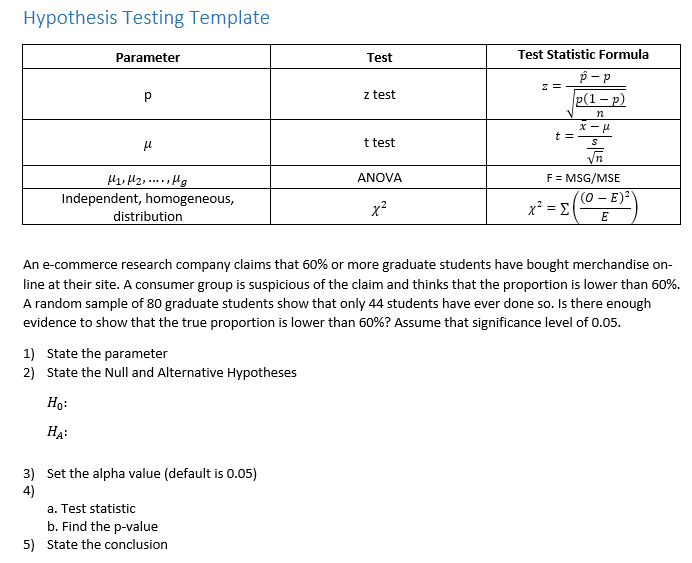
Z Formula For Hypothesis
A z test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distributionz test tests the mean of a distribution.

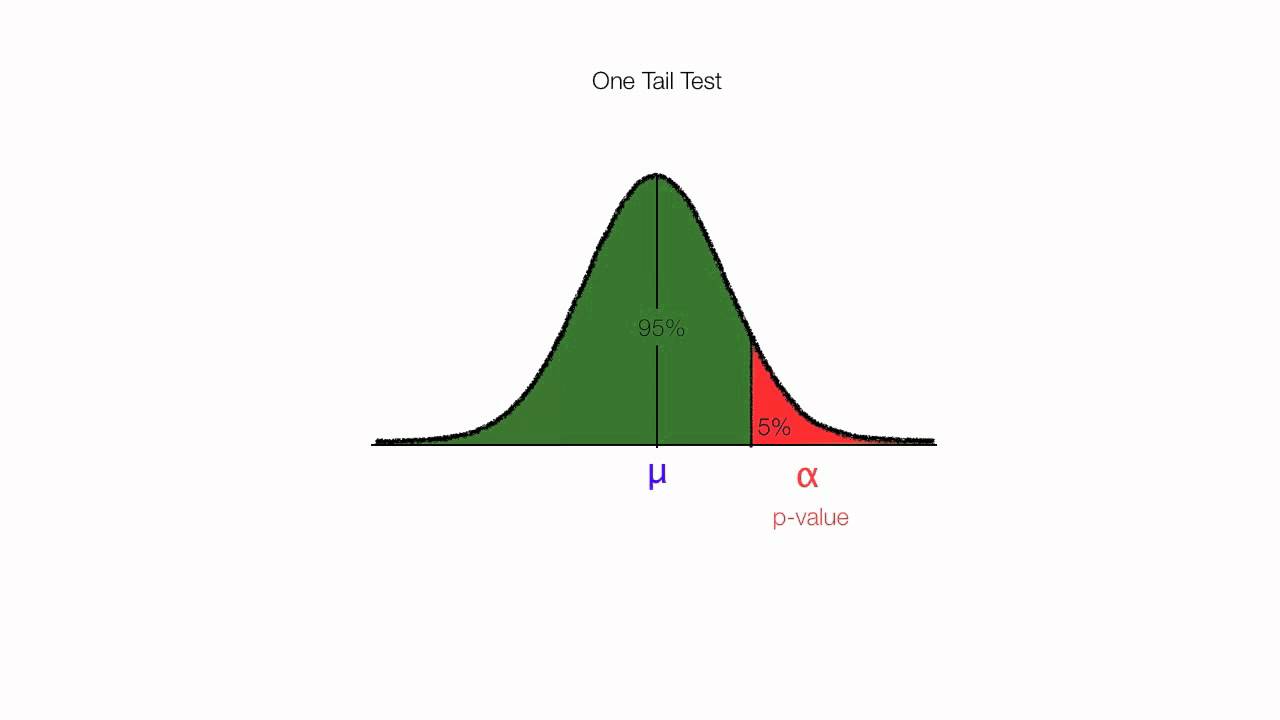
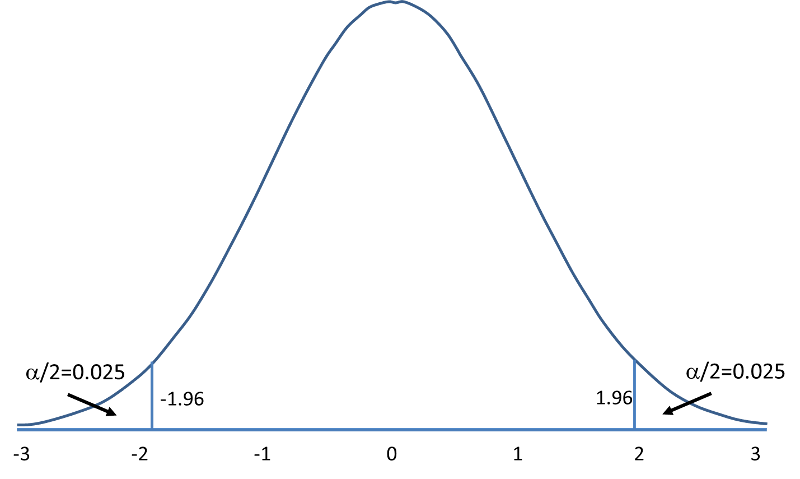
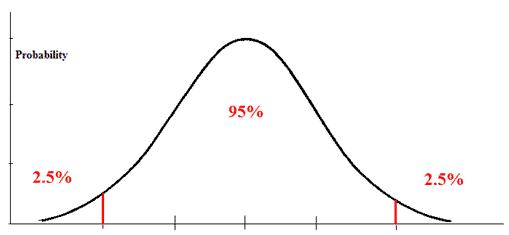
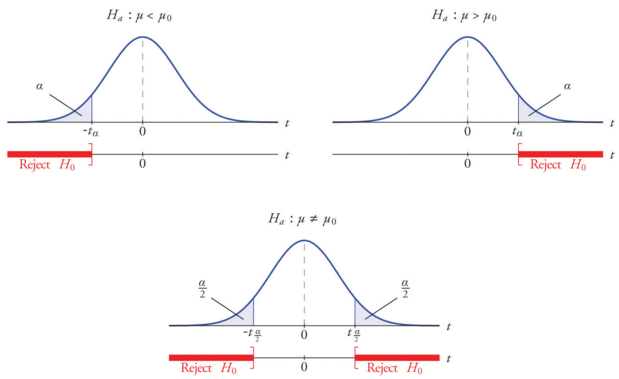
Z formula for hypothesis. We know that we have a 2 tailed hypothesis and we are working with an alpha level of 005. Formula to calculate z test in statistics. To make our decision we will again draw a distribution.
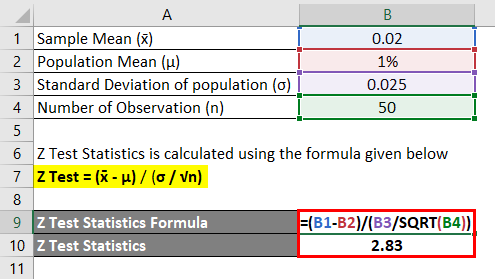
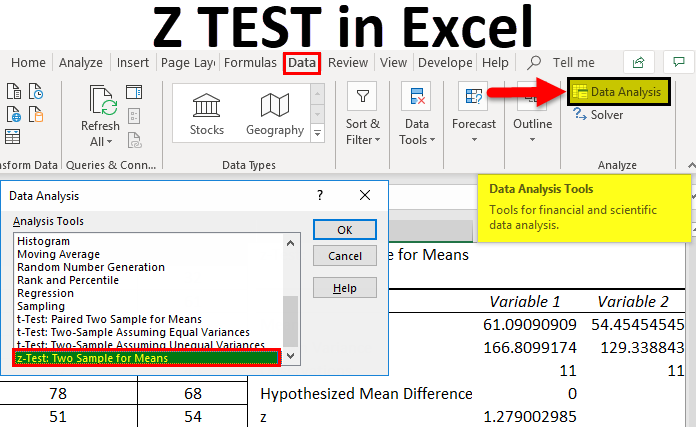
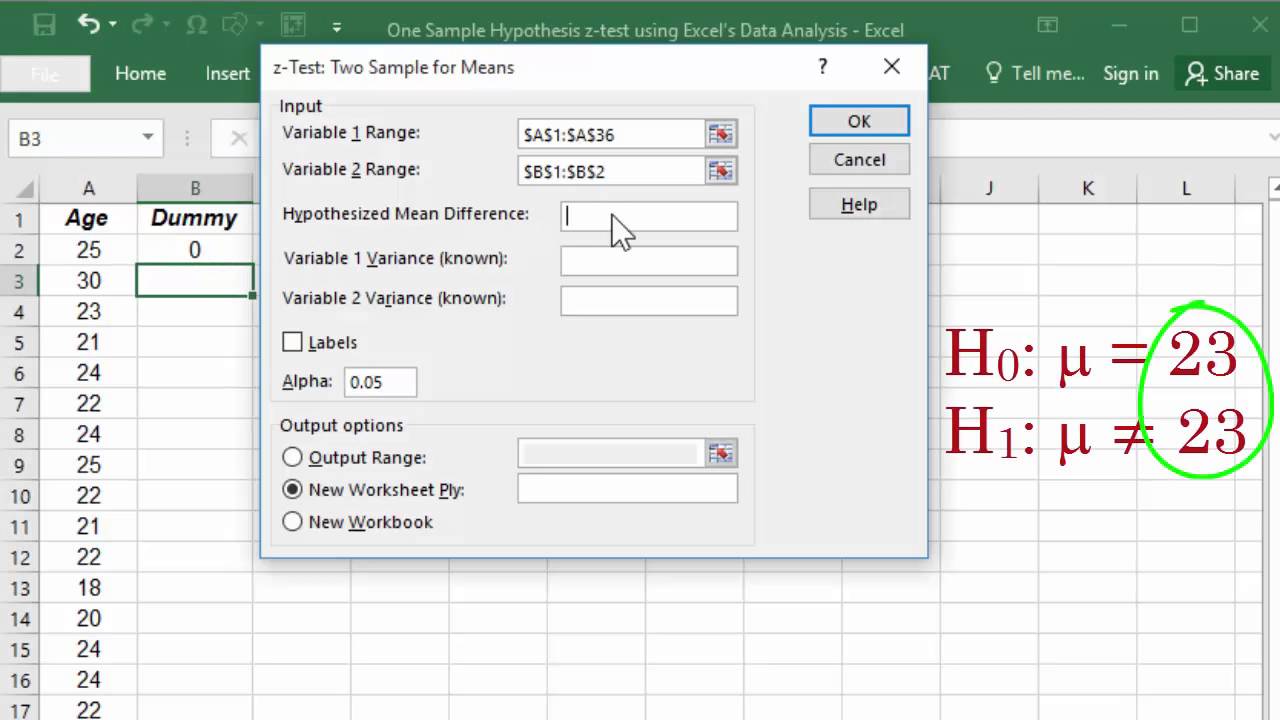
So from the above calculation investors will come to conclusion and he will reject the null hypothesis because the result of z is greater than 196 and come to an analysis that the average daily return of the stock is more than 1. Z test in statistics refers to the hypothesis test which is used to determine whether the two samples means calculated are different in case the standard deviations are available and the sample is large. Statistical software such as excel can be used to perform hypothesis tests.
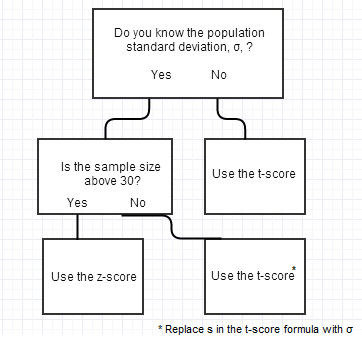
There are multiple steps to conduct a hypothesis test and many of these require statistical calculations. The z test is also a hypothesis test in which the z statistic follows a normal distribution. Also find the z score from z table given the level of significance and mean.
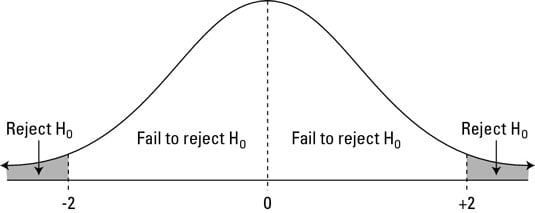
Now however we have a critical z score of 196. Examples of hypothesis testing formula with excel template. For finding out hypothesis of a given sample we conduct a z test.
The null hypothesis for this test is that both sample proportions come from the same population proportion. For each significance level in the confidence interval the z test has a single critical value for example 196 for 5 two tailed which makes it more convenient than the students t test whose. The z test is best used for greater than 30 samples because under the central limit theorem as the.
The z test formula is given as. Large zfracoverlinex mu fracsigma sqrtn where overlinex is the sample mean mu is the population mean. We will see how the excel function ztest tests hypotheses about an unknown population mean.
Again the formula for the test is based on the z statistic but it takes on a different form since it involves two samples. Usually in hypothesis testing we compare two sets by comparing against a synthetic data set and idealized model.

Z T And F Tests Making Inferences From Experimental Sample To Population Using Statistical Tests Ppt Download
slideplayer.com













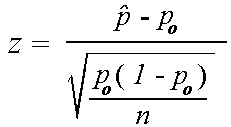

:max_bytes(150000):strip_icc()/Clipboard01-5c94e6b446e0fb00010ae8ed.jpg)










/HypothesisTestinginFinance1_2-1030333b070c450c964e82c33c937878.png)






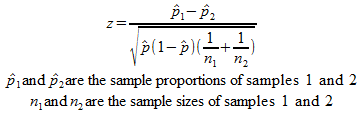












/ZTest-56a8faa45f9b58b7d0f6ea64.jpg)

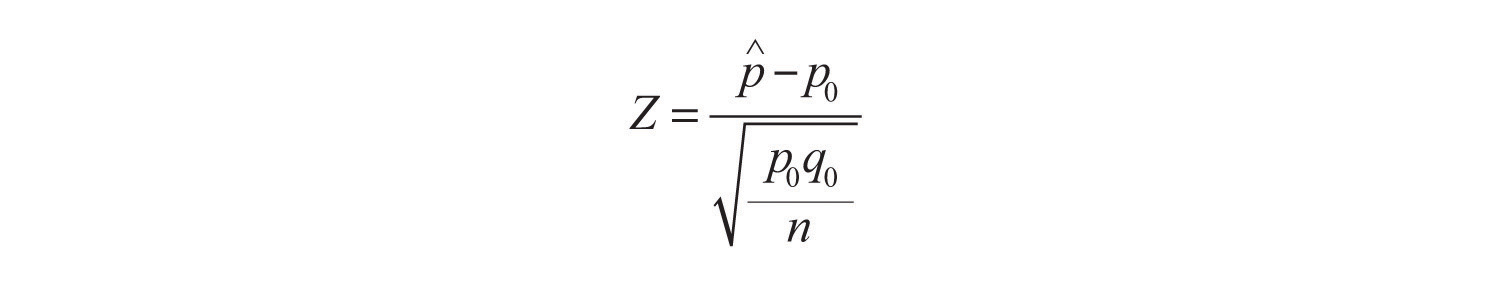









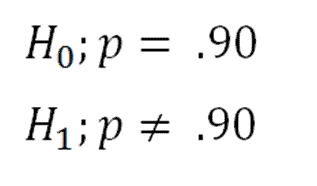



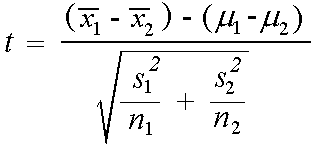





:max_bytes(150000):strip_icc()/comparing-two-proportions-57b5a4e33df78cd39c67380b.jpg)